According to the finite element method, the soil is schematized with springs whose characteristics depend on the elastic modules of the soil, differentiating those in compression by those in tension. Bowles proposed to calculate, in an approximate way, the value of Ks (reaction module that is connected to the stiffness of the soil) on the basis of the bearing capacity of the foundations. The method provides directly, after building the global stiffness matrix and the vector of nodal loads, the deformations and, from these, the moments and the nodal reactions. For the calculation of the bulkhead proceed as follows:
(a) Calculation of the side pressure to the dredge line
(b) Set a depth for the first attempt
(c) Estimation of the value of Ks below the dredge line
(d) Arrangement of nodes where are assigned the stiffness of the springs
(e) Establish a trial section and calculation of the inertia moment of the section
(f) Stiffness calculation of any anchors
(g) Assemble the global stiffness matrix
(h) Assembly of the vector of nodal loads
(i) Calculation of the nodal displacements
The calculation is solved by an iterative procedure. The iterations continue until the displacements on the dredge line, between two cycles of calculation, are included in a tolerance value specified. The environment for the management of certain data related to implementation of the finite element method is the following:
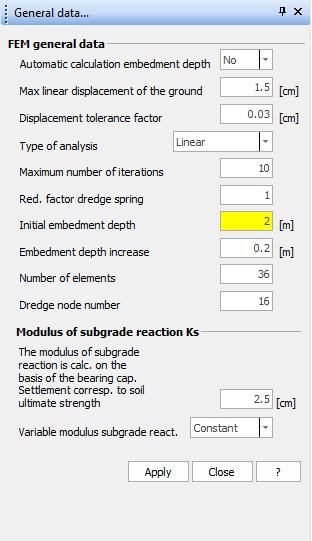
FEM general data
•Automatic calculation of embedment depth: Select Yes for automatic computation of the embedment depth and No to let the input of the embedment depth at the choice of the user.
•Max linear displacement of the ground: Expressed in cm. Is the maximum displacement that allows to consider the ground in the linear range. After this displacement, the spring which represents the soil can not be considered in elastic-linear field (depends very much on the characteristics of the soil, in any case Order of magnitude = 1/2 cm).
•Displacement tolerance factor: Expressed in cm. Is the tolerance set to define the exit condition from analysis iterations (depends on certain analysis conditions and geometry of the structure, Order of magnitude = 1/200 of the maximum size of the structure for example bulkhead height).
•Type of analysis: Defines whether the analysis conducted is linear or non-linear (Is recommended non-linear analysis when the statics of the problem depends predominantly on the geotechnical aspect of the problem).
•Maximum number of iterations: It's the maximum number of iterations to be carried out to find a solution to the movement. Above this limit, the solution is deemed not found (In contexts related to practice the 'order of magnitude iterations = 5/10).
•Red. factor dredge spring: It's a dimensionless factor that goes to multiply the reaction modulus of the spring located at the bottom of the excavation. Must assume the value less than or at most equal to 1.
•Initial embedment depth: Embedment depth for the first trial, expressed in m. (Order of magnitude = 0.1 / 0.2 of the height of the bulkhead).
•Embedment depth increase: Is the increase for the current embedment depth with which to search for a balanced solution (Magnitude = 0.1 / 0.2 of the height of the bulkhead).
•Number of elements: Must be between 10 and 50. Is the number of finite elements in which is discretized the entire bulkhead (it should realize a rational description, not too sparse, to avoid gross errors in the solution, not too thick, to avoid that the calculation times are extended considerably).
•Dredge node number: Defines the node associated with the bottom of the excavation. The higher this number will be, bigger the number of finite elements that discretize the upper part of the bulkhead will be.
Modulus of subgrade reaction Ks
•Settlement corresponding to soil ultimate strength: Is the displacement associated to the bearing capacity, expressed in cm.
•Variable modulus of subgrade reaction: Is possible to take into account the variability of the axial stiffness of the springs, which simulate the presence of the ground, with the depth or even conduct the analysis with a constant modulus.
Using the F.E.M. method can be checked an embedment depth assigned by the user (for example, to verify existing bulkheads), by selecting No for the automatic calculation of the embedment depth and set to 1 the maximum number of iterations (imposed automatically) and assign the desired initial embedment depth.
|
© GeoStru