La probabilità
La teoria della probabilità è lo studio matematico della probabilità.
I matematici si riferiscono alle probabilità come a numeri nell'intervallo da 0 a 1, assegnati ad "eventi" la cui ricorrenza è casuale.
La probabilità è un numero associato ad un evento (risultante dall'osservazione di un esperimento) che può o meno verificarsi.
Probabilità a priori o classica
Se N è il numero totale di casi dello spazio campionario di una variabile aleatoria ed n il numero di casi favorevoli per i quali si realizza l’evento A, la probabilità a priori di A è data da:
![]()
La probabilità a priori può assumere un valore compreso tra 0 e 1. Una probabilità pari a 0 indica che l’evento è impossibile, una probabilità pari ad 1 indica che l’evento è certo.
Probabilità frequentista
Se m è il numero di prove in cui si è verificato l’evento A su un totale di M prove, la probabilità di A è data da:
![]()
Il limite che compare in questa definizione non va inteso in senso matematico, ma in senso sperimentale: il valore vero della probabilità si trova solo effettuando un numero infinito di prove.
Indicatori di una distribuzione statistica
La descrizione dei dati di un campione statistico viene fatta determinando la distribuzione delle frequenze relative, che contiene implicitamente tutte le informazioni che dal campione possiamo trarre.
Gli indicatori sono dei parametri che descrivono quantitativamente gli aspetti generali della distribuzione statistica.
•Nella teoria della probabilità la funzione di probabilità o funzione di distribuzione, di una variabile casuale discreta x è una funzione di variabile reale che assegna ad ogni valore possibile di x la probabilità dell'evento.
•Il valore atteso m (chiamato anche media o speranza) di una variabile casuale reale x, è un numero che formalizza l'idea euristica di valore medio di un fenomeno aleatorio ed è definito come:
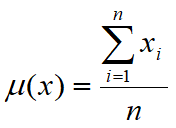
•La varianza di una variabile aleatoria x è un numero Var(x) che fornisce una misura di quanto siano vari i valori assunti dalla variabile, ovvero di quanto si discostino dalla media m. La varianza di x è definita come il valore atteso del quadrato della variabile aleatoria centrata. In statistica viene spesso preferita la radice quadrata della varianza di x, lo scarto quadratico medio (o deviazione standard) indicato con la lettera σ. Per questo motivo la varianza viene indicata con σ2. In statistica si utilizzano solitamente due stimatori per la varianza su un campione di cardinalità n:
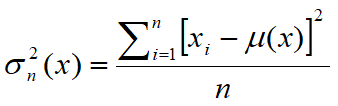 e
e 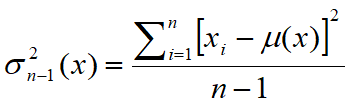
Lo stimatore sn-1 ha un valore atteso uguale proprio alla varianza, al contrario, lo stimatore sn ha un valore atteso diverso dalla varianza. Una giustificazione del termine n-1 è data dalla necessità di stimare anche la media. Se la media μ è nota, lo stimatore sn diventa corretto.
•A partire dallo scarto quadratico medio si definisce anche il coefficiente di variazione o la deviazione standard relativa come il rapporto tra lo scarto tipo e la media aritmetica dei valori:
![]()
Questo nuovo parametro (spesso usato in forma percentuale) consente di effettuare confronti tra dispersioni di dati di tipo diverso, indipendentemente dalle loro quantità assolute.
Il modo in cui si distribuisce la probabilità di una variabile aleatoria dipende da molti fattori, e, come vi sono infiniti possibili grafici di funzioni, così si possono avere infinite modalità diverse per le distribuzioni di probabilità.
Le più significative distribuzioni di probabilità sono:
1) Distribuzione normale;
2) Distribuzione lognormale;
3) Distribuzione t di Student.
La distribuzione normale
La variabile casuale Normale (detta anche variabile casuale Gaussiana o curva di Gauss) è una variabile casuale continua con due parametri, indicata tradizionalmente con:
![]()
Si tratta di una delle più importanti variabili casuali, soprattutto continue, in quanto è, la base di partenza per le altre variabili casuali ( Chi Quadrato, t di Student, F di Snedecor ecc..).
La variabile casuale gaussiana è caratterizzata dalla seguente funzione di densità di probabilità, cui spesso si fa riferimento con la dizione curva di Gauss o gaussiana:
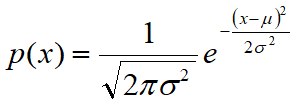
dove x rappresenta la grandezza di cui si deve calcolare la probabilità
![]()
e dove µ e σ rappresentano la popolazione media e lo scarto quadratico medio (o deviazione standard). L'equazione della funzione di densità è costruita in modo tale che l'area sottesa alla curva rappresenti la probabilità. Perciò, l'area totale è uguale a 1.
La curva che descrive l’andamento della probabilità è simmetrica ed è centrata intorno al valore medio.
Nella terminologia statistica il punto in cui la curva assume il suo valore massimo viene chiamato moda, il valore invece per il quale alla grandezza x è associata una probabilità del 50% viene definito mediana.
Nella distribuzione normale, media, moda e mediana coincidono.
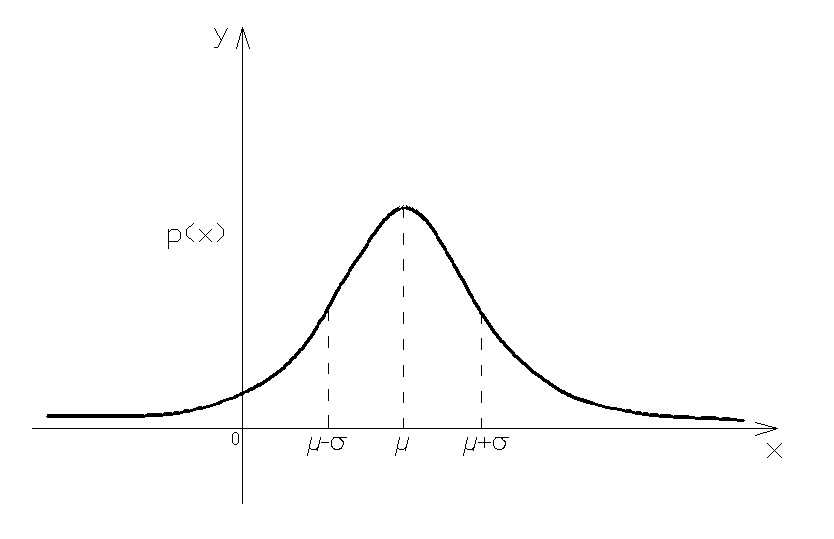
Ricorrendo alla standardizzazione (statistica) della variabile casuale, cioè alla trasformazione tale per cui risulta:
![]()
dove la variabile risultante
![]()
ha anch'essa distribuzione normale con parametri μ = 0 e σ = 1, la curva di gauss può essere scritta come:
![]()
Il valore caratteristico potrà essere valutato tramite l’espressione:
![]()
Con una probabilità del 5% Z (da tabella) è pari a -1.645, perciò l’espressione precedente si può riscrivere come:
![]()
Dividendo ambo i membri per la media µ la relazione diventa:
![]()
La distribuzione lognormale
Una variabile casuale x ha distribuzione lognormale, con parametri µ e s, se ln(x) ha distribuzione normale con media µ e deviazione standard s.
Equivalentemente:
![]()
e
![]()
dove y è distribuita normalmente con media µ e deviazione standard s.
Il parametro µ può essere un qualsiasi reale, mentre s dev'essere positivo.
La curva di distribuzione della probabilità assume la seguente forma:
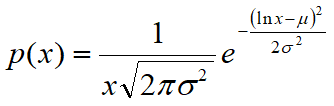
A causa dell’asimmetria della curva, i valori di media, moda e mediana non coincidono, a differenza di quanto accade invece nella distribuzione normale. Il punto di massimo della curva si trova, infatti, spostato verso sinistra rispetto al valore medio.
La distribuzione di Student
La distribuzione t di Student considera le relazioni tra media e varianza in campioni di piccole dimensioni, estratti da una popolazione normalmente distribuita, utilizzando la varianza del campione.
Data una popolazione distribuita normalmente, si estrae un campione casuale di n osservazioni e si calcola la variabile aleatoria t, definita dalla seguente equazione:
![]()
dove s è la varianza campionaria.
t segue una legge t di Student con n-1 gradi di libertà. La quantità al numeratore si chiama errore standard campionario.
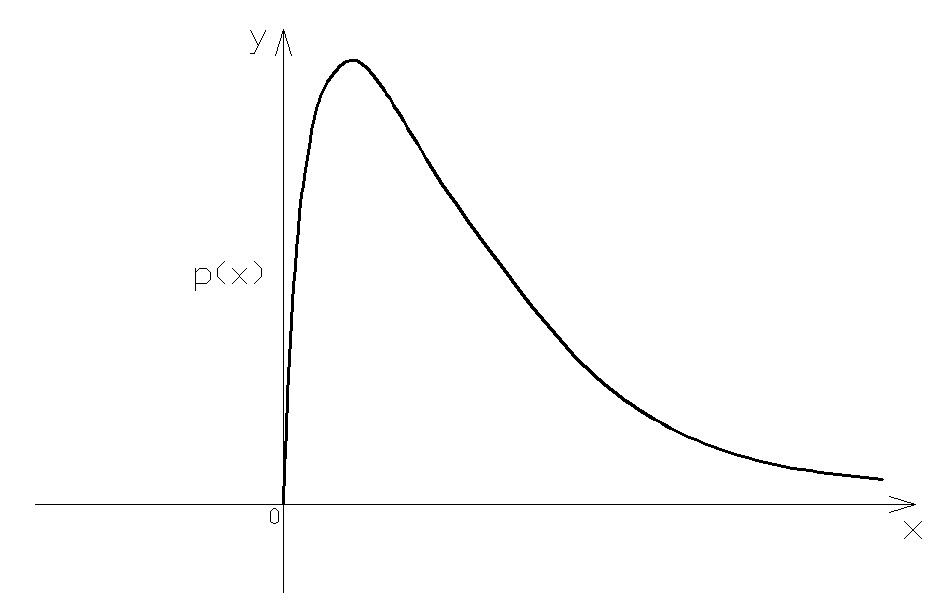
La forma della distribuzione dipende dai gradi di libertà, cioè dalla numerosità del campione. Per n grande (>30) t tende ad una normale.
Regola del tre-sigma
In una distribuzione normale il 99,73% delle misure ricadono a una distanza dal valore medio di tre volte la deviazione standard, cioè c’è una probabilità del 99,73% che una misura estratta a caso dalla popolazione giaccia nell’intervallo ±3s rispetto alla media m.
Una volta noto il valore più elevato misurato nella popolazione dato da:
![]()
e quello più basso:
![]()
la deviazione standard della popolazione può essere calcolata come:
![]()
Teorema di Bayes
Il teorema di Bayes, proposto da Thomas Bayes, deriva da due teoremi fondamentali delle probabilità: il teorema della probabilità composta e il teorema della probabilità assoluta. Viene spesso usato per calcolare le probabilità a posteriori (posterior probabilities) date delle osservazioni.
Questo teorema può essere espresso dalla forma seguente:
![]()
Dove:
P(A\B) è la probabilità che si verifichi l’evento A se si verifica l’evento B;
P(B\A) è la probabilità che si verifichi l’evento B se si verifica l’evento A;
P(A) è la probabilità a priori che si verifichi l’evento A;
P(B\A’) è la probabilità che si verifichi l’evento B se non si verifica l’evento A=1-P(B\A);
P(A’) è la probabilità che non si verifichi l’evento A=1-P(A).
|
©GeoStru