CARGA ÚLTIMA DE LA LOSA
La carga última de una cimentación superficial se puede definir haciendo referencia a aquel valor máximo de la carga para el cual en ningún punto del subsuelo se alcanza la condición de rotura (método de Frolich), o bien haciendo referencia a aquel valor de la carga, mayor que el precedente, para el cual el fenómeno de rotura se ha extendido hacia un amplio volumen del suelo (método de Prandtl y sucesivos).
Prandtl estudió el problema de la rotura de un semiespacio elástico por efecto de una carga aplicada sobre su superficie con referencia al acero, caracterizando la resistencia a rotura con una ley tipo:
τ = c+σ∙tanφ válida también para suelos
Las hipótesis y las condiciones introducidas por Prandtl son las siguientes:
- Material ingrávido, por lo tanto γ = 0.
- Comportamiento rígido – plástico.
- Resistencia a rotura del material expresable con la relación: τ = c+σ∙tanφ
- Carga uniforme, vertical y aplicada sobre una franja de longitud infinita y de ancho 2b (estado de deformación plana).
- Tensiones tangenciales nulas al contacto entre la franja de carga y la superficie límite del semiespacio.
En el acto de rotura se produce la plastificación del material contenido entre la superficie límite del semiespacio y la superficie GFBCD (Véase Fig. 2).
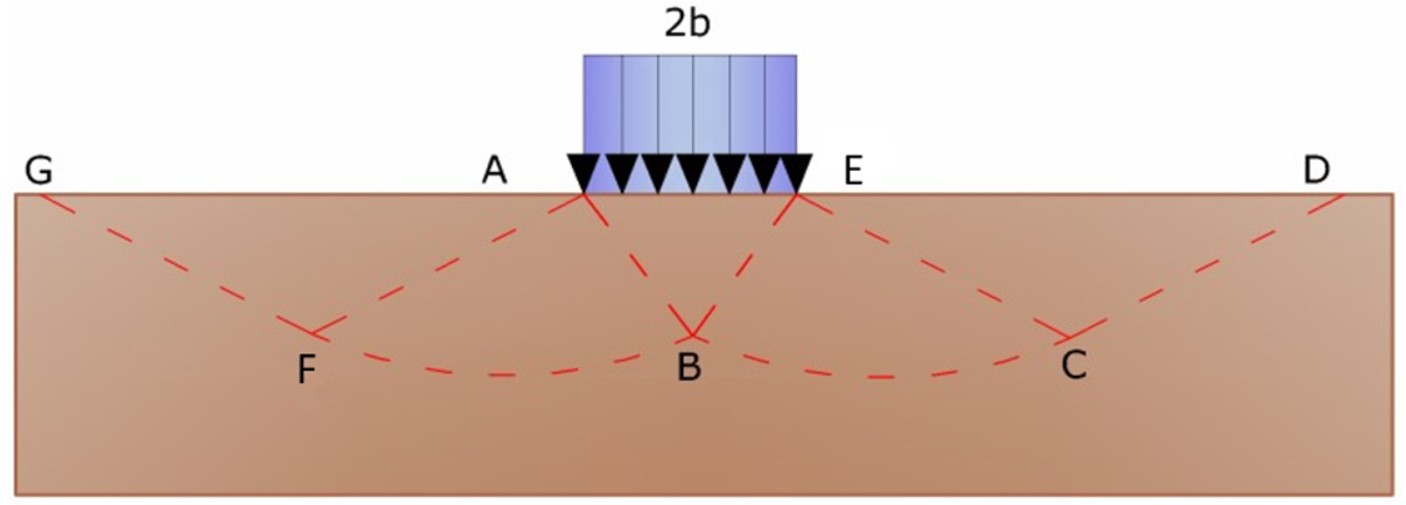
Figura 2. - Mecanismo de rotura de Prandtl
Ya identificado el volumen de terreno llevado a la rotura por la carga última, ésta se puede calcular escribiendo la condición de equilibrio entre las fuerzas agentes sobre cualquier volumen de terreno delimitado por debajo de cualquiera de las superficies de deslizamiento.
Si llega entonces a una ecuación q =B∙c, donde el coeficiente B depende solamente del ángulo de rozamiento φ del terreno.
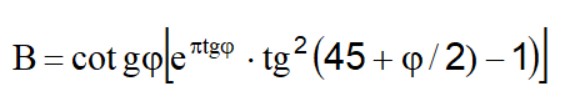
Para φ =0 el coeficiente B resulta igual a 5.14, por lo tanto q=5.14∙c.
En el caso particular de suelo sin cohesión (c=0, γ≠0) resulta q = 0, según la teoría de Prandtl, no sería posible aplicar ninguna carga sobre la superficie límite de un terreno incoherente.
Esta teoría, si bien no es aplicable en la práctica, ha dado impulso a todas las investigaciones y métodos de cálculo posteriores.
De hecho Caquot se puso en las mismas condiciones de Prandtl, excepto que la franja de carga ya no se aplica sobre la superficie límite del semiespacio, sino que a una profundidad h, con h ≤ 2b; el terreno comprendido entre la superficie y la profundidad h tiene las siguientes características: γ≠0, φ =0, c=0, representa un medio con peso pero sin resistencia.
Resolviendo las ecuaciones de equilibrio se obtiene la expresión:
q=A∙γ1 + B∙c
que sin duda es un paso adelante con respecto a Prandtl, pero que aún no refleja la realidad.
Método de Terzaghi (1955)
Terzaghi, continuando el estudio de Caquot, aportó algunos cambios para tomar en cuenta las características efectivas del conjunto obra de cimentación-terreno.
Bajo la acción de la carga transmitida por la cimentación, el terreno que está en contacto con la esa cimentación tiende a escaparse lateralmente, pero se lo impiden las resistencias tangenciales que se desarrollan entre la cimentación y el terreno. Esto comporta un cambio del estado tensional en el terreno colocado directamente por debajo de la cimentación.
Para tomar esto en cuenta, Terzaghi asigna a los lados AB y EB de la cuña de Prandtl una inclinación y con respecto a la horizontal, seleccionando el valor de y en función delas características mecánicas del terreno al contacto terreno-obra de cimentación.
Así, la suposición g2 =0 para el terreno por debajo de la cimentación se supera; admitiendo que las superficies de rotura permanezcan inalteradas, la expresión de la carga última será:
q = A∙γ1∙h + B∙c+C∙γ∙b
Donde C es un coeficiente función del ángulo de rozamiento φ del terreno por debajo del plano de cimentación y del ángulo φ anteriormente definido; b es la semi anchura de la franja.
Además, basándose en datos experimentales, Terzaghi pasa del problema plano al problema espacial, introduciendo factores de forma.
Terzaghi hizo además otra contribución sobre el efectivo comportamiento del terreno.
En el método de Prandtl se supone un comportamiento rígido-plástico del terreno, mientras que Terzaghi admite este comportamiento en los suelos muy compactos.
En éstos, de hecho, la curva cargas-asientos presenta un primer tracto rectilíneo, seguido por un breve tracto curvilíneo (comportamiento elasto-plástico). La rotura es instantánea y el valor de la carga última resulta claramente identificado (rotura general).
En un suelo muy suelto, en cambio, la relación cargas-asientos presenta un tracto curvilíneo acentuado ya desde las cargas más bajas debido al efecto de una rotura progresiva del terreno (rotura local); por lo tanto, la identificación de la carga última no es tan clara y evidente como en el caso de los suelos compactos.
Al hacer explícitos los coeficientes de la fórmula anterior, la fórmula de Terzaghi se puede escribir así:
q = c∙Nc∙sc+γ∙D∙Nq+0.5∙γ∙B∙Nγ∙sγ
Donde:
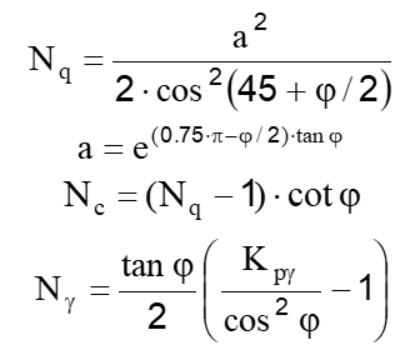
Con:

Fórmula de Meyerhof (1963)
Meyerhof propuso una fórmula similar a la de Terzaghi para calcular la carga última. La diferencia consiste en la introducción de nuevos coeficientes de forma.
Introdujo un coeficiente sq que multiplica el factor Nq, factores de profundidad di y de pendencia ii para aquellos casos en que la carga transmitida a la cimentación sea inclinada sobre la vertical.
Los valores de los coeficientes N se obtuvieron de Meyerhof, suponiendo varios arcos de prueba BD (véase mecanismo Prandtl), considerando valores aproximados del corte que se produce en el terreno por encima del plano de cimentación. Los factores de forma tomados de Meyerhof se presentan a continuación, junto con la expresión de l fórmula.
q = c∙Nc∙sc∙dc + γ∙D∙Nq∙dq + 0.5∙γ∙B∙Nγ∙sγ∙dγ
Donde:

Fórmula de Hansen (1970)
Se trata de una extensión más de la fórmula de Meyerhof; las extensiones consisten en la introducción de algunos términos para tomar en cuenta la inclinación de la cimentación y la inclusión de la cimentación en un talud.
La fórmula de Hansen vale para cualquier relación D/B, incluso cimentaciones superficiales. El mismo autor introdujo coeficientes para poder interpretar mejor el comportamiento real de la cimentación, sin los cuales, de hecho, se tendría un aumento demasiado fuerte de la carga última con la profundidad.
Factores de profundidad
Para valores de D/B<1:
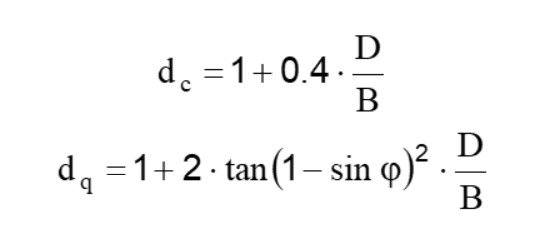
Para valores de D/B>1:
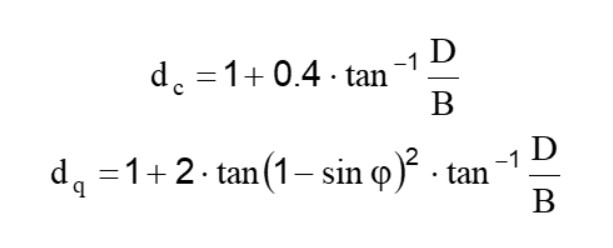
En caso de φ=0

Factores de forma
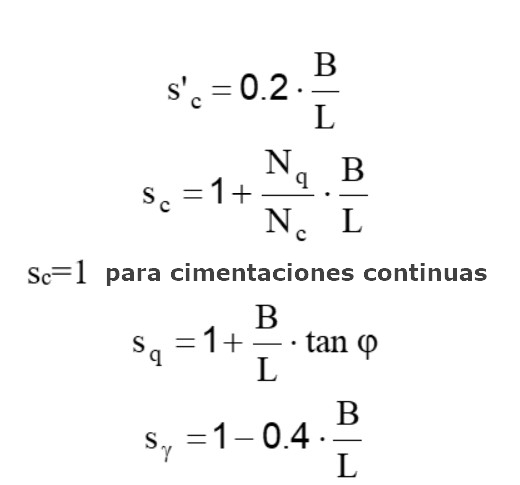
Factores de inclinación del terreno (cimentación sobre talud inclinado)
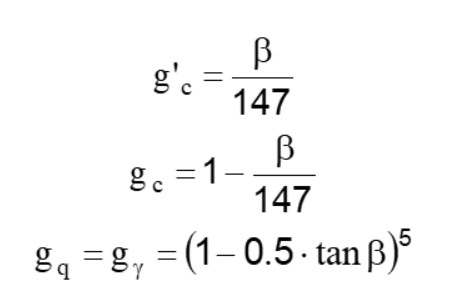
En los factores siguientes, las expresiones con comillas (') valen cuando φ=0.
Fórmula de Vesic (1975)
La fórmula de Vesic es análoga a la fórmula de Hansen, con Nq y Nc como en la fórmula de Meyerhof y Ng como a continuación:
![]()
Los factores de forma y de profundidad que aparecen en las fórmulas de capacidad de carga son iguales a las propuestas por Hansen; algunas de las diferencias están en los factores de inclinación del terreno (cimentación en talud).
ASIENTOS ELÁSTICOS
Los asientos de una cimentación rectangular de tamaño BxL colocada sobre la superficie de un semiespacio elástico se pueden calcular con base en una ecuación basada en la teoría de la elasticidad (Timoshenko y Goodier, 1951):
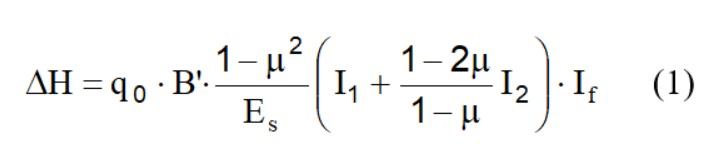
Donde:
q0 Intensidad de la presión de contacto
B' Tamaño mínimo del área reactiva,
E e m Parámetros elásticos del terreno.
Ii Coeficientes de influencia dependientes de: L'/B', espesor del estrato H, coeficiente de Poisson
m, Profundidad del plano de cimentación D.
Los coeficientes I1 y I2 se pueden calcular utilizando las ecuaciones de Steinbrenner (1934) (V. Bowles), en función dela relación L'/B' y H/B, utilizando B'=B/2 y L'=L/2 para los coeficientes correspondientes al centro y B'=B y L'=L para los coeficientes correspondientes al borde.
El coeficiente de influencia IF se deriva de las ecuaciones de Fox (1948), que indican el asiento se reduce con la profundidad en función del coeficiente de Poisson y dela relación L/B.
Para simplificar la ecuación (1) se introduce el coeficiente IS:
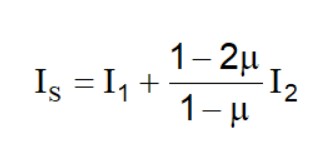
El asiento del estrato de espesor H vale:
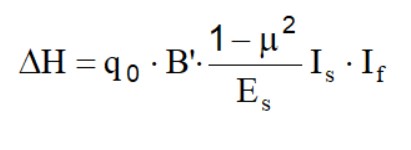
Para aproximar mejor los asientos, se subdivide la base de apoyo de forma tal que el punto esté en corresponda con una esquina externa común a varios rectángulos. En la práctica, para el cálculo de los asientos en el centro, se multiplica por un factor igual a 4 y por un factor igual a 1 para los asientos en el borde.
Al calcular los asientos se considera una profundidad del bulbo tensiones igual a 5B, si el substrato rocoso se encuentra en una profundidad mayor. Para este propósito se considera substrato rocoso aquel estrato que tenga un valor de E igual a 10 veces del estrato de arriba. El módulo elástico para terrenos estratificados se calcula como promedio ponderado de los módulos elásticos de los estratos afectados por el asiento inmediato.
© GeoStru