CARICO LIMITE DELLA PLATEA
Il carico limite di una fondazione superficiale può essere definito con riferimento a quel valore massimo del carico per il quale in nessun punto del sottosuolo si raggiunge la condizione di rottura (metodo di Frolich), oppure con riferimento a quel valore del carico, maggiore del precedente, per il quale il fenomeno di rottura si è esteso ad un ampio volume del suolo (metodo di Prandtl e successivi).
Prandtl ha studiato il problema della rottura di un semispazio elastico per effetto di un carico applicato sulla sua superficie con riferimento all'acciaio, caratterizzando la resistenza a rottura con una legge del tipo:
τ = c+σ∙tanφ valida anche per i terreni.
Le ipotesi e le condizioni introdotte dal Prandtl sono le seguenti:
- Materiale privo di peso e quindi γ = 0.
- Comportamento rigido – plastico.
- Resistenza a rottura del materiale esprimibile con la relazione: τ = c+σ∙tanφ
- Carico uniforme, verticale ed applicato su una striscia di lunghezza infinita e di larghezza 2b (stato di deformazione piana).
- Tensioni tangenziali nulle al contatto fra la striscia di carico e la superficie limite del semispazio.
All'atto della rottura si verifica la plasticizzazione del materiale racchiuso fra la superficie limite del semispazio e la superficie GFBCD (Vedi Fig. 2).
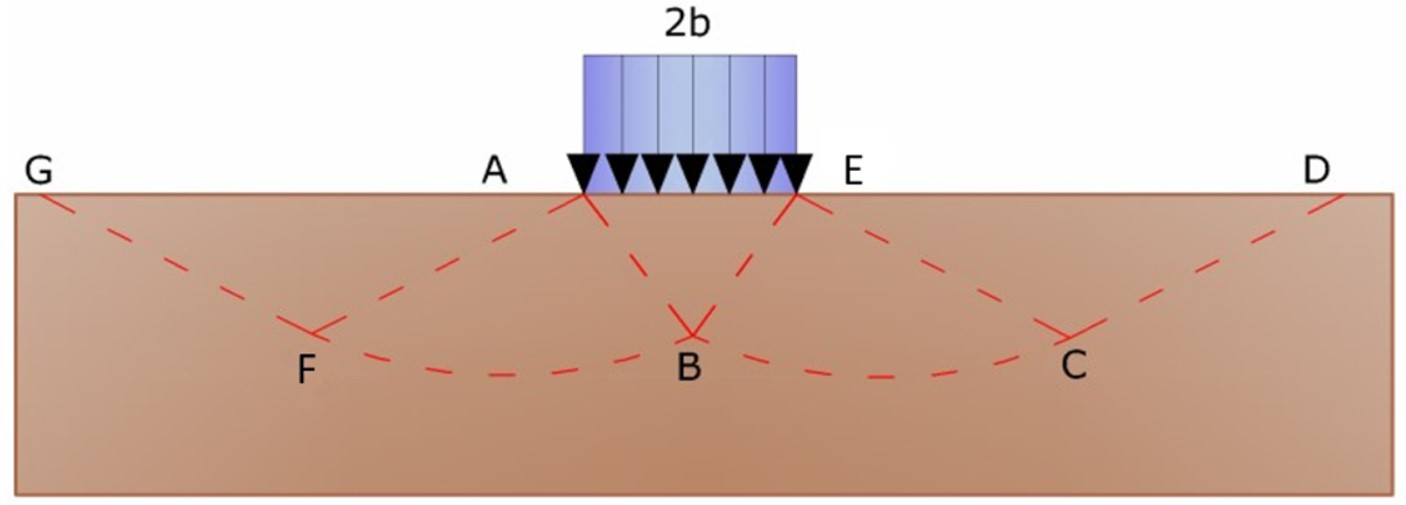
Figura 2. - Meccanismo di rottura di Prandtl
Individuato così il volume di terreno portato a rottura dal carico limite, questo può essere calcolato scrivendo la condizione di equilibrio fra le forze agenti su qualsiasi volume di terreno delimitato in basso da una qualunque delle superfici di scorrimento.
Si arriva quindi ad una equazione q =B∙c, dove il coefficiente B dipende soltanto dall'angolo di attrito φ del terreno.
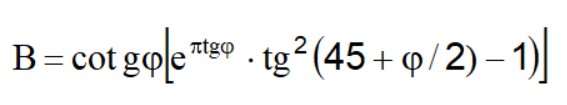
Per φ =0 il coefficiente B risulta pari a 5.14, quindi q=5.14∙c.
Nell'altro caso particolare di terreno privo di coesione (c=0, γ≠0) risulta q = 0, secondo la teoria di Prandtl, non sarebbe dunque possibile applicare nessun carico sulla superficie limite di un terreno incoerente.
Questa teoria, anche se non applicabile praticamente, ha dato inizio a tutte le ricerche ed i metodi di calcolo successivi.
Infatti Caquot si pose nelle stesse condizioni di Prandtl ad eccezione del fatto che la striscia di carico non è più applicata sulla superficie limite del semispazio, ma a una profondità h, con h ≤ 2b; il terreno compreso tra la superficie e la profondità h ha le seguenti caratteristiche: γ≠0, φ =0, c=0, rappresenta un mezzo dotato di peso ma privo di resistenza.
Risolvendo le equazioni di equilibrio si arriva all'espressione:
q=A∙γ1 + B∙c
che è sicuramente è un passo avanti rispetto a Prandtl, ma che ancora non rispecchia la realtà.
Metodo di Terzaghi (1955)
Terzaghi, proseguendo lo studio di Caquot, ha apportato alcune modifiche per tenere conto delle effettive caratteristiche dell'insieme opera di fondazione-terreno.
Sotto l'azione del carico trasmesso dalla fondazione il terreno che si trova a contatto con la fondazione stessa tende a sfuggire lateralmente, ma ne è impedito dalle resistenze tangenziali che si sviluppano fra la fondazione ed il terreno. Ciò comporta una modifica dello stato tensionale nel terreno posto direttamente al di sotto della fondazione; per tenerne conto Terzaghi assegna ai lati AB ed EB del cuneo di Prandtl una inclinazione y rispetto all'orizzontale, scegliendo il valore di y in funzione delle caratteristiche meccaniche del terreno al contatto terreno-opera di fondazione.
L'ipotesi g2 =0 per il terreno sotto la fondazione viene così superata ammettendo che le superfici di rottura restino inalterate, l'espressione del carico limite è quindi:
q = A∙γ1∙h + B∙c+C∙γ∙b
in cui C è un coefficiente che risulta funzione dell'angolo di attrito φ del terreno posto al di sotto del piano di posa e dell'angolo φ prima definito; b è la semilarghezza della striscia.
Inoltre, basandosi su dati sperimentali, Terzaghi passa dal problema piano al problema spaziale introducendo dei fattori di forma.
Un ulteriore contributo è stato apportato da Terzaghi sull' effettivo comportamento del terreno.
Nel metodo di Prandtl si ipotizza un comportamento del terreno rigido-plastico, Terzaghi invece ammette questo comportamento nei terreni molto compatti.
In essi, infatti, la curva carichi-cedimenti presenta un primo tratto rettilineo, seguito da un breve tratto curvilineo (comportamento elasto-plastico); la rottura è istantanea ed il valore del carico limite risulta chiaramente individuato (rottura generale).
In un terreno molto sciolto invece la relazione carichi-cedimenti presenta un tratto curvilineo accentuato fin dai carichi più bassi per effetto di una rottura progressiva del terreno (rottura locale); di conseguenza l'individuazione del carico limite non è così chiara ed evidente come nel caso dei terreni compatti.
Esplicitando i coefficienti della formula precedente, la formula di Terzaghi può essere scritta:
q = c∙Nc∙sc+γ∙D∙Nq+0.5∙γ∙B∙Nγ∙sγ
Dove:
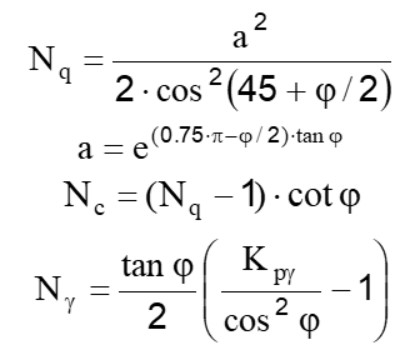
Con:

Formula di Meyerhof (1963)
Meyerhof propose una formula per il calcolo del carico limite simile a quella di Terzaghi; le differenze consistono nell'introduzione di ulteriori coefficienti di forma.
Egli introdusse un coefficiente sq che moltiplica il fattore Nq, fattori di profondità di e di pendenza ii per il caso in cui il carico trasmesso alla fondazione è inclinato sulla verticale.
I valori dei coefficienti N furono ottenuti da Meyerhof ipotizzando vari archi di prova BD (v. meccanismo Prandtl), considerando valori approssimati del taglio che si sviluppa nel terreno al di sopra del piano di posa. I fattori di forma tratti da Meyerhof sono di seguito riportati, insieme all'espressione della formula.
q = c∙Nc∙sc∙dc + γ∙D∙Nq∙dq + 0.5∙γ∙B∙Nγ∙sγ∙dγ
Dove:

Formula di Hansen (1970)
È una ulteriore estensione della formula di Meyerhof; le estensioni consistono nell'introduzione di alcuni termini per tener conto dell'inclinazione della fondazione e dell'inserimento della fondazione in un pendio.
La formula di Hansen vale per qualsiasi rapporto D/B, quindi sia per fondazioni superficiali, lo stesso autore introdusse dei coefficienti per meglio interpretare il comportamento reale della fondazione, senza di essi, infatti, si avrebbe un aumento troppo forte del carico limite con la profondità.
Fattori di profondità
Per valori di D/B<1:
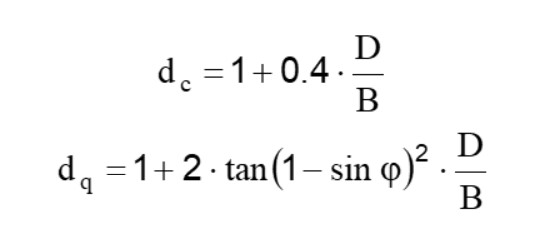
Per valori di D/B>1:
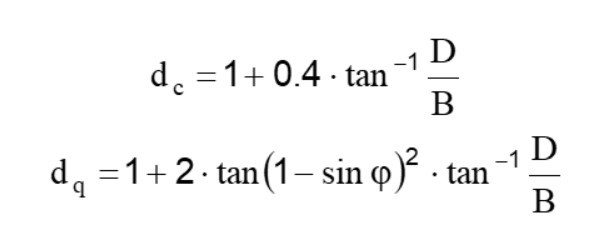
Nel caso di φ=0

Fattori di forma

Fattori di inclinazione del terreno (fondazione su pendio inclinato)
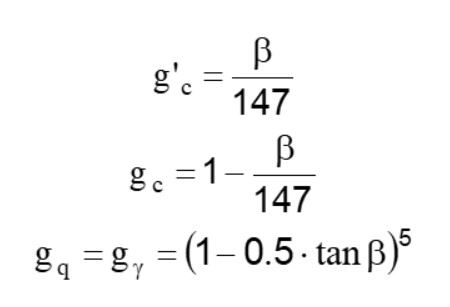
Nei fattori seguenti le espressioni con apici (') valgono quando φ=0.
Formula di Vesic (1975)
La formula di Vesic è analoga alla formula di Hansen, con Nq ed Nc come per la formula di Meyerhof ed Ng come sotto riportato:
![]()
I fattori di forma e di profondità che compaiono nelle formule del calcolo della capacità portante sono uguali a quelli proposti da Hansen; alcune differenze sono invece riportate nei fattori di inclinazione del terreno (fondazione su pendio).
CEDIMENTI ELASTICI
I cedimenti di una fondazione rettangolare di dimensioni BxL posta sulla superficie di un semispazio elastico si possono calcolare in base aduna equazione basata sulla teoria dell'elasticità (Timoshenko e Goodier, 1951):
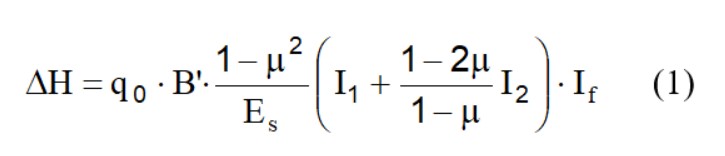
Dove:
q0 Intensità della pressione di contatto
B' Minima dimensione dell'area reagente,
E e m Parametri elastici del terreno.
Ii Coefficienti di influenza dipendenti da: L'/B', spessore dello strato H, coefficiente di Poisson
m, profondità del piano di posa D.
I coefficienti I1 e I2 si possono calcolare utilizzando le equazioni fornite da Steinbrenner (1934) (V. Bowles), in funzione del rapporto L'/B' ed H/B, utilizzando B'=B/2 e L'=L/2 per i coefficienti relativi al centro e B'=B e L'=L per i coefficienti relativi al bordo.
Il coefficiente di influenza IF deriva dalle equazioni di Fox (1948), che indicano il cedimento si riduce con la profondità in funzione del coefficiente di Poisson e del rapporto L/B.
In modo da semplificare l'equazione (1) si introduce il coefficiente IS:
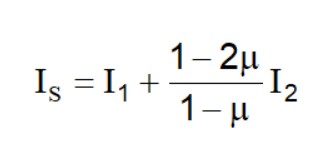
Il cedimento dello strato di spessore H vale:
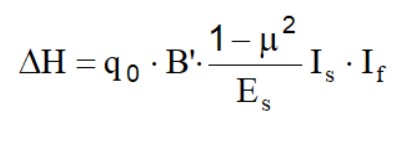
Per meglio approssimare i cedimenti si suddivide la base di appoggio in modo che il punto si trovi in corrispondenza di uno spigolo esterno comune a più rettangoli. In pratica si moltiplica per un fattore pari a 4 per il calcolo dei cedimenti al centro e per un fattore pari a 1 per i cedimenti al bordo. Nel calcolo dei cedimenti si considera una profondità del bulbo delle tensioni pari a 5B, se il substrato roccioso si trova ad una profondità maggiore. A tal proposito viene considerato substrato roccioso lo strato che ha un valore di E pari a 10 volte dello strato soprastante. Il modulo elastico per terreni stratificati viene calcolato come media pesata dei moduli elastici degli strati interessati dal cedimento immediato.
© GeoStru