METODO PDR (POULOS, DAVIS & RANDOLPH)
Si tratta di un metodo che consente di eseguire un’analisi di interazione tra una platea, dotata di rigidezza Kplatea e carico limite Qplatea,lim ed un gruppo di pali, avente rigidezza Kpali e carico limite Qpali,lim.
Questi due sistemi si combinano a costituire una platea pilata di rigidezza Kmista e carico limite Qmista,lim.
Il metodo si basa su alcune ipotesi semplificative:
-Carichi solo verticali e centrati
-Platea infinitamente rigida
-Comportamento elastico lineare per platea-terreno e per pali-terreno
Per la curva carico-cedimento, il metodo ipotizza che il comportamento della platea e del gruppo di pali sia di tipo elastico lineare fino raggiungimento dei rispettivi carichi limite, legame costitutivo di tipo trilineare (vedi Fig. 3).
La trilineare è definita da due punti notevoli:
-Il punto A, nel quale si esaurisce la resistenza del gruppo di pali.
-Il punto B, nel quale la resistenza della fondazione mista nel suo complesso è interamente mobilitata, ovvero è stata sfruttata anche l’intera capacità portante della platea.
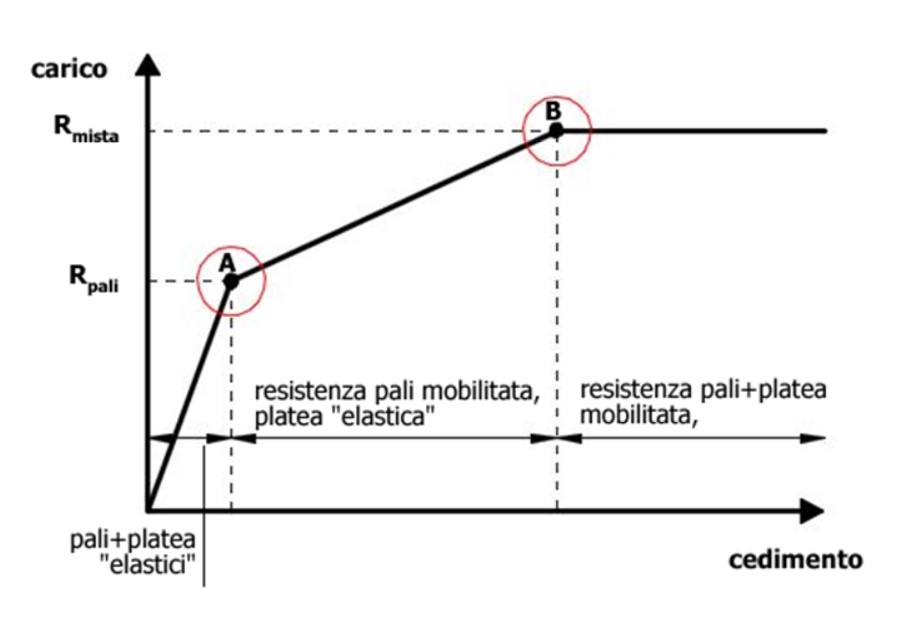
Figura 3. - Legame costitutivo trilineare della fondazione mista
Nel primo tratto della curva pali e platea collaborano, quindi la pendenza è pari alla rigidezza della platea pilata Kmista. Nel secondo tratto la pendenza è pari invece a quella della sola platea, Kplatea, essendosi esaurito il contributo dei pali.
Il carico da considerare P va valutato con la combinazione quasi permanente allo SLE.
La legge con la quale varia il cedimento della fondazione fino al punto A (platea e pali sono in campo elastico) è:
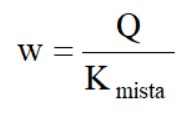
Oltre il punto A ogni incremento di carico può essere assorbito dalla sola platea, la resistenza dei pali si è completamente mobilitata mentre la platea si trova in campo elastico. Il cedimento sarà dato dalla relazione:
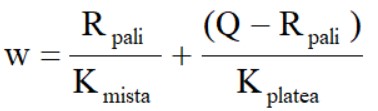
Raggiunto il punto B (P = Rmista) sia la resistenza dei pali sia quella della platea si sono completamente mobilitati e la fondazione mista collassa.
Il calcolo della rigidezza del gruppo dei pali si esegue sfruttando la relazione proposta da Fleming et al. (1992):
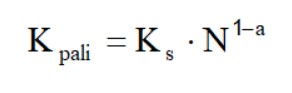
Dove Ks è la rigidezza del singolo palo mentre il termine si ottiene dalla relazione seguente interpolando i valori dal grafico.
a = astandard∙ainterasse∙aPoisson∙aEP∙ap
La Ks è la rigidezza del singolo palo si ricava come:

© GeoStru