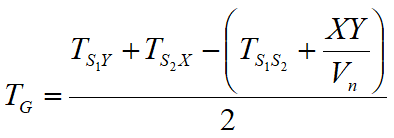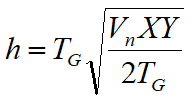Le indagini di sismica a rifrazione consentono di interpretare la stratigrafia del sottosuolo attraverso il principio fisico del fenomeno della rifrazione totale di un'onda sismica che incide su una discontinuità, individuata fra due corpi aventi proprietà meccaniche diverse (orizzonte rifrattorio). La condizione fondamentale per eseguire studi di sismica a rifrazione è quella per cui la successione di strati da investigare sia caratterizzata da velocità sismiche crescenti all'aumentare della profondità. In questo modo si possono valutare fino a 4 o 5 orizzonti rifrattori differenti.
Le prove si basano sulla misura dei tempi di percorso delle onde elastiche per le quali, ipotizzando le superfici di discontinuità estese rispetto alla lunghezza d'onda o, comunque, con deboli curvature, i fronti d'onda sono rappresentati mediante i relativi raggi sismici. L'analisi si avvale, poi, del principio di Fermat e della legge di Snell.
Il principio di Fermat stabilisce che il raggio sismico percorre la distanza tra sorgente e rilevatore seguendo il percorso per cui il tempo di tragitto è minimo. Per tale principio, dato un piano che separa due mezzi con caratteristiche elastiche diverse, il raggio sismico è quello che si estende lungo un piano perpendicolare alla discontinuità contente sia la sorgente che il ricevitore.
La legge di Snell è una formula che descrive le modalità di rifrazione di un raggio sismico nella transizione tra due mezzi caratterizzati da diversa velocità di propagazione delle onde o, equivalentemente, da diversi indici di rifrazione. L'angolo formato tra la superficie di discontinuità e il raggio sismico è chiamato angolo di incidenza θi mentre quello formato tra il raggio rifratto e la superficie normale è detto angolo di rifrazione θr. La formulazione matematica è:
|
|
(1) |
Dove v1 e v2 sono le velocità dei due mezzi separati dalla superficie di discontinuità.
Per v1 > v2 si ha che θi > θr e la sismica a rifrazione non è attuabile poiché il raggio rifratto andrebbe ad inclinarsi verso il basso. Per v1<v2 si ha che θi < θr ed esiste un angolo limite di incidenza per cui θr = 90° ed il raggio rifratto viaggia parallelamente alla superficie di discontinuità. L'espressione che definisce l'angolo limite è:
|
|
(2) |
Il modo più semplice per analizzare i dati di rifrazione è quello di costruire un diagramma tempi-distanze in cui l'origine del sistema di riferimento è posto in corrispondenza della sorgente di generazione delle onde elastiche. In ascissa sono rappresentate le posizioni dei geofoni ed in ordinata i tempi dei primi arrivi. Ai geofoni più vicini alla sorgente giungono per primi gli impulsi che hanno seguito il percorso diretto in un tempo T dato dalla relazione
|
|
(3) |
dove xi è la distanza tra il punto di energizzazione e il punto di rilevazione.
L'equazione (3) rappresenta una retta che passa per l'origine degli assi tempi-distanze e il suo coefficiente angolare consente di calcolare la velocità V1 del primo mezzo come
|
|
(4) |
I tempi di arrivo dei raggi rifratti, nel diagramma tempi-distanze, si dispongono secondo una retta che avrà pendenza minore di quella delle onde dirette.
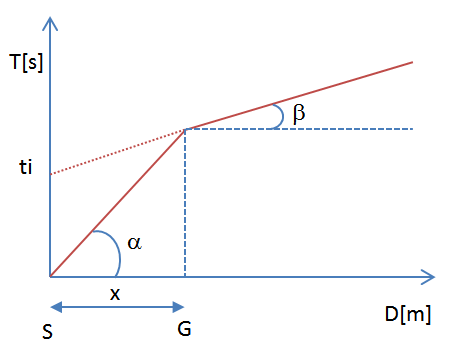
La curva tempi-distanze tende ad avere un andamento regolare secondo una spezzata i cui vertici sono i chiamati punti di ginocchio e rappresentano, fisicamente, la condizione in cui si verifica l'arrivo contemporaneo delle onde dirette e rifratte. Per ciascuno di segmenti individuati si determina, dunque, il tempo di ritardo ti che rappresenta la differenza tra il tempo che il raggio sismico impiega a percorrere un tratto alla velocità propria dello strato in cui si trasmette ed il tempo che impiegherebbe a viaggiare lungo la componente orizzontale di quel tratto alla massima velocità raggiunta in tutto il percorso di rifrazione.
Graficamente il tempo di ritardo è dato dall'intersezione della retta che comprende un segmento della curva tempi-distanze con l'asse dei tempi.
Infine, dalla conoscenza dei tempi ti è possibile ricavare gli spessori dei rifrattori mediante la relazione:
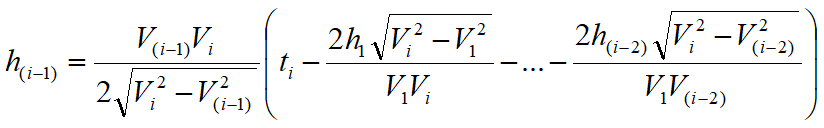 (5)
(5)
In situazioni morfologiche complesse può essere utilizzato come metodo di elaborazione il Metodo Reciproco Generalizzato (Generalized Reciprocal Method) discusso da Palmer nel 1980.
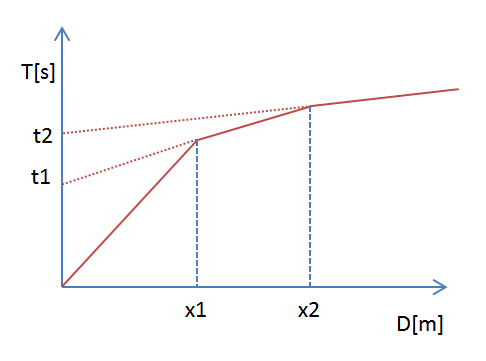
Il metodo è basato sulla ricerca di una distanza intergeofonica virtuale XY tale che i raggi sismici che partono da punti di energizzazione simmetrici rispetto allo stendimento, arrivino al geofono posto in posizione X e a quello posto in posizione Y provenendo da un medesimo punto del rifrattore.
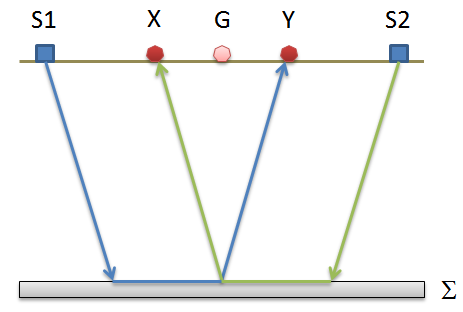
Il primo passo operativo è quello di costruire un diagramma tempi-distanze individuando nei sismogrammi ottenuti dai dati di campagna i primi arrivi delle onde sismiche. Per determinare la distanza XY ottimale è necessario considerare più punti di energizzazione tanto agli estremi quanto all'interno dello stendimento. Ciò permette di individuare con maggiore accuratezza i tempi relativi ad un medesimo rifrattore utili a caratterizzare le dromocrone, fondamentali all'interpretazione. Nelle interpretazioni multi strato, la generazione delle dromocrone può sfruttare tecniche di phantoming per sopperire alla mancanza dei dati per alcuni rifrattori.
Dalla costruzione delle dromocrone è possibile determinare la funzione velocità secondo l'equazione
dove TS1Y e TS2X sono i tempi di percorrenza dei raggi sismici per giungere, rispettivamente, dalla sorgente S1 ad X e dalla sorgente S2 ad Y mentre Ts1s2 è il tempo di tragitto tra i due punti di scoppio S1 ed S2, esternamente simmetrici rispetto allo stendimento. Tv è il tempo calcolato su un geofono G posto tra X ed Y, non necessariamente coincidente con la posizione di un geofono dello stendimento.
Il calcolo della funzione Tv viene eseguito per ogni valore di XY compreso tra zero e metà dello stendimento con variazione pari alla distanza reale tra i geofoni dello stendimento. La migliore retta di regressione delle funzioni velocità ottenute, permette di determinare l'XY ottimo e la velocità del rifrattore che è ricavata dal coefficiente angolare.
Per mezzo della funzione tempo-profondità è possibile trovare la profondità del rifrattore espressa in unità di tempo. L'espressione di tale funzione è:
Dove Vn è la velocità del rifrattore.

Analogamente a quanto avviene per la funzione velocità si determinano diverse funzioni tempo-profondità per l'insieme dei valori XY di studio. Tra le funzioni trovate, quella che presenta la maggiore articolazione compete al valore di XY ottimo.
Infine, è possibile determinare lo spessore del rifrattore in corrispondenza delle posizioni dei geofoni G mediante la relazione:
|
|
(8) |
h rappresenta la profondità minima dal geofono G dunque la morfologia del rifrattore è definita dall'inviluppo delle semicirconferenze di raggio h.
Uno dei principali vantaggi del G.R.M. è che il fattore di conversione della profondità è relativamente insensibile alle inclinazioni fino a circa 20°
© Geostru