Al punto 7.4.3.1 le NTC definiscono parete come "elemento strutturale di supporto per altri elementi che ha una sezione trasversale caratterizzata da un rapporto tra dimensione massima e minima in pianta superiore a 4. Si definisce parete di forma composta l'insieme di più pareti semplici collegate in modo da formare sezioni a L, T, U, I ec. Una parete accoppiata consiste di due o più pareti singole collegate tra loro da travi duttili (travi di accoppiamento) distribuite in modo regolare lungo l'altezza. ...".
Negli edifici in c.a. si utilizza spesso la tipologia strutturale mista telaio-parete in cui, sempre citando le NTC, "la resistenza alle azioni orizzontali è affidata in parte ai telai ed in parte alle pareti, singole o accoppiate...".
Nel presente programma tutti gli elementi pareti sopra citati vengono modellati in maniera simile ai pilastri (§ 1.3) cioè con elementi monodimensionali (beam) utilizzando opportunamente i conci rigidi per il collegamento delle stesse pareti tra loro o con gli altri elementi del telaio tridimensionale (wide columns model).
In figura 13.1 oltre a due pareti accoppiate (e complanari) poste in corrispondenza dei nodi K, L è stata inserita una pilastrata a partire dal nodo M. In questo caso la modellazione delle due pareti è identica a quella di due pilastri di identica sezione con l'unica differenza che nelle pareti non vengono generati in automatico conci rigidi in quanto si presuppone che la rigidezza della parete sia molto maggiore rispetto a quella delle travi di accoppiamento che in essa si innestano al punto da poterne trascurare l'influenza.
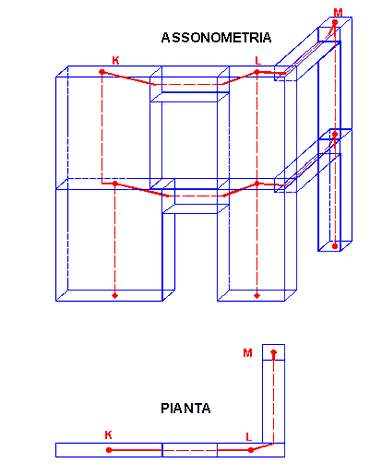
Figura 13.1 - Pareti accoppiate
La trave di accoppiamento che collega i nodi K-M viene generata automaticamente come una qualsiasi altra trave e presenta quindi un tratto deformabile rappresentato in figura dall'asse baricentrico (linea rossa tratteggiata) e da due conci rigidi internamente al perimetro delle pareti. La trave che collega il pilastro M con la parete L avendo l'asse del tratto deformabile disallineato rispetto alla congiungente dei nodi M, L va posizionata (vedi Capitolo 2) assegnando al concio rigido che fa capo al nodo L gli opportuni valori valori di offset (eccentricità) in modo da ottenere per il tratto deformabile il voluto allineamento (evidenziato nella vista in pianta di figura 13.1). Occorre comunque fare attenzione all'incastro della trave M-L nella parete L quanto più la larghezza della parete risulta maggiore della larghezza di innesto della trave: si consiglia, stante l'incertezza sul grado di incastro effettivo della trave nella parete, di incrementare adeguatamente le armature della trave (ottenute dal programma) sia in campata che all'incastro.
Le pareti previste in programma possono presentare sezioni solo di forma rettangolare le cui dimensioni vengono assegnate nello stesso archivio dei pilastri (archivio pilastri-pareti) specificandone però la tipologia. Ciò permetterà al programma di effettuare il calcolo di dimensionamento e verifica delle armature specificatamente previsto dalle NTC per le pareti.
Molti programmi di calcolo discretizzano le pareti mediante elementi finiti bidimensionali (Shell, Isoshell, etc.). L'utilizzo di questi elementi finiti nelle correnti applicazione spesso crea più problemi di quanti ne risolve:
•Le norme richiedono per la verifica delle pareti (punto 7.4.4.5.2 NTC) la valutazione degli sforzi assiali, di taglio e flettenti nelle varie sezioni orizzontali. Utilizzando elementi bidimensionali è necessario, una volta effettuato il calcolo, integrare i risultati dei nodi (sforzi di piastra e membrana) presenti nelle singole sezioni di calcolo.
•Il collegamento delle pareti discretizzate ad elementi monodimensionali (beam) è molto più problematico. Si consideri ad esempio la semplicissima struttura in figura 14.1 costituita da una mensola modellata con elementi bidimensionali che porta in sommità una mensola caricata con una forza F. La totazione della mensola (elemento beam) nel nodo di incastro alla parete può risultare enorme (controllo del drilling assente) o risultare variabile a seconda dell'algoritmo di drilling implementato. Il momento flettente trasmesso dalla mensola determina, inoltre, uno stato tensionale nella parete quasi sempre errato (l'esempio è tratto da [9] Cap. 4 cui si rimanda per una trattazione completa dell'argomento).
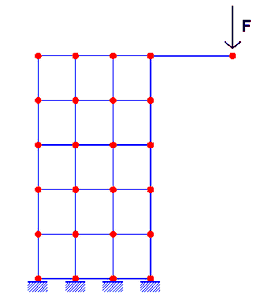
Figura 14.1 - Parete FEM+Mensola
•L'uso degli elementi bidimensionali incrementa notevolmente il numero di gradi di libertà (e quindi delle equazioni risolventi) nell'edificio rallentando il calcolo (sia statico che modale) e sopratutto rendendo più difficile il controllo dei risultati.
•La rigidezza alla traslazione orizzontale (l'aspetto statico più importante che in generale determina l'inserimento delle pareti nella progettazione strutturale) della parete modellata con elementi monodimensionali è molto prossima a quella della stessa parete modellata con elementi bidimensionali. Si consideri a tal fine la parete a 6 piani riportata nel manuale di validazione del noto programma ETABS [12] le cui dimensioni sono state trasformate da inches in cm. Assumendo un modulo elastico E= 3000 ksi = 206843 daN/cm² il carico in sommità F = 100 k = 444482 daN produce i seguenti spostamenti orizzontali (sempre in sommità):
ETABS SAP90 Edifici ca
0.259 cm 0.262 cm 0.266 cm
Risultati molto vicini da non giustificare il ricorso ad elementi finiti bidimensionali.
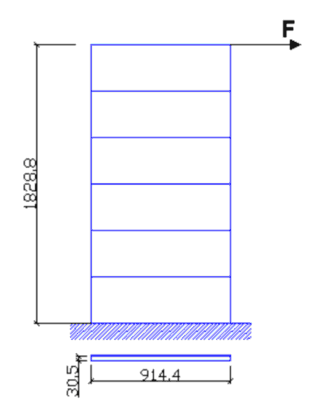
Figura 15.1 - Parete a 6 piani