In questo programma i solai vengono considerati elementi strutturali "secondari" nel senso indicato nel punto 7.2.3 delle NTC e cioè tali elementi vengono progettati per i soli carichi verticali al di fuori del programma mentre all'interno del programma tridimensionale la loro resistenza viene ignorata mentre vengono valutati i carichi da essi trasmessi alle travi nonchè le masse riportate nei nodi si competenza. In ogni caso il contributo degli elementi secondari alla rigidezza complessiva dell'edificio soggetto all'azione sismica orizzontale di progetto non può superare il 15% della rigidezza degli elementi resistenti principali. Data l'aleatorietà del confronto tra rigidezze M. Fardis (cfr. [18]) consiglia di effettuare il confronto sulla base degli spostamenti orizzontali di piano: se ad ogni piano la differenza tra gli spostamenti sismici dell'edificio, modellato prima in presenza e poi in assenza della rigidezza degli elementi secondari, risulta inferiore al 15% gli elementi non considerati nell'analisi potranno definirsi secondari.
Negli impalcati orizzontali dei correnti edifici in c.a. i solai dotati di soletta continua gettata in opera impediscono ai nodi ricadenti negli impalcati stessi di mobilitare tutti i 6 gradi di libertà posseduti da ognuno di essi. Al riguardo nel § 7.2.6 delle NTC si afferma che:
"Gli orizzontamenti possono essere considerati infinitamente rigidi nel loro piano, a condizione siano realizzati in cemento armato, oppure in latero-cemento con soletta in c.a. di almento 40 mm di spessore, ..., purchè le aperture presenti non ne riducano significativamente la rigidezza."
La notevolte rigidezza estensionale di tali impalcati (assunta infinita nel modello di calcolo) comporta le seguenti importanti conseguenze nel calcolo strutturale:
•Gli spostamenti nei gradi di libertà traslazionali in direzione X, Y e quello rotazionale intorno all'asse Z di tutti i nodi sono uguali e quindi vengono assegnati ad un unico nodo aggiuntivo nel piano, detto nodo master, che potrebbe in teoria essere un punto qualsiasi del piano ma che nell'ambito dell'analisi dinamica a masse concentrate viene assunto coincidente con il baricentro delle masse concentrate dei nodi di piano. Nell'elementare telaio tridimensionale con piano rigido illustrato in figura 3.1 sono evidenziati i gradi di libertà attivi dei 4 nodi originari dell'impalcato (1-2-3-4) e del nodo master (5) aggiunto. In tutto si hanno 15 incognite di spostamento contro le 6x4= 24 che si avrebbero considerando l'impalcato deformabile. Aumentando il numero di nodi nel piano le incognite di spostamento si riducono alla metà + 3 con grande riduzione dei tempi di elaborazione.
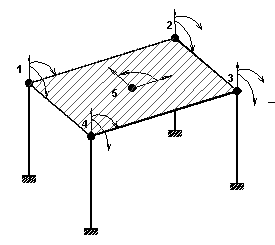
Figura 3.1 - Piano rigido
•Le deformazioni assiali delle travi di piano possono essere assunte nulle per l'infinita rigidezza dell'impalcato e quindi anche nulli vengono considerati i relativi sforzi normali.
•I solai considerati rigidi nel piano orizzontale impediscono la deformazione flessionale delle travi nel piano di impalcato per cui la corrispondente componente dello sforzo flettente può assumersi nulla. Le travi dell'impalcato possono così essere progettate a flessione retta (con taglio ed eventuale torsione) con grande semplificazione nel calcolo e nella rappresentazione grafica delle armature. Infatti i comuni esecutivi delle travi di piano in c.a. ne visualizzano solo le barre longitudinali superiori ed inferiori con riferimento ad una o più travi sullo stesso allineamento (travate). Nel caso di travi soggette a pressoflessione deviata, invece, tale semplice rappresentazione grafica sarebbe insufficiente.
Si consideri il piano definito dagli 8 nodi di figura 4.1 in cui:
•i nodi 1-2-3-4 definiscono una falda inclinata rigida nel proprio piano per la presenza di idoneo solaio o soletta in ca;
•i nodi 5-6-7-8 definiscono una zona di impalcato orizzontale anch'essa rigida nel proprio piano;
•i nodi 2-5-4-7 definiscono una zona vuota dell'impalcato.
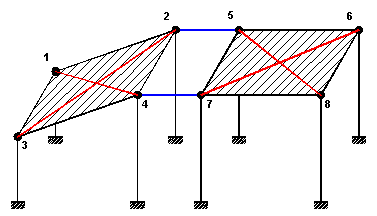
Figura 4.1 - Piano deformabile
La quota in elevazione notevolmente ridotta (rispetto agli altri nodi) dei nodi 1 e 3 fa sì che l'impalcato non possa considerarsi orizzontale e di conseguenza a rigore non dovrebbe essere attivata l'opzione di piano rigido. Se tuttavia nella zona vuota dell'impalcato fosse invece disposto un solaio estensionalmente rigido come gli altri e le travi non fossero spingenti (tali cioè da poter considerare trascurabili gli sforzi normali nelle stesse e trascurabili gli spostamenti differenziali orizzontali tra i nodi del piano), l'ipotesi di piano rigido potrebbe essere assunta accettando una certa approssimazione numerica.
La particolare conformazione del vuoto nell'impalcato di figura 4.1 impedisce di poter utilizzare l'opzione di piano rigido al piano in questione. Infatti in presenza di forze orizzontali (sismiche o prodotte dal vento) le due zona rigide dell'impalcato si sposterebbero nel piano in maniera sensibilmente differente a causa della notevole deformabilità nel piano orizzontale delle travi 2-5 e 4-7 (indicate in blu nella figura 4.1) da progettare accuratamente in presso-tenso flessione deviata (cosa impossibile se le travi vengono incorporate in un piano rigido dove le travi vengono analizzate solo in flessione retta con sforzo normale nullo).
Nell'ambito dei piani deformabili nasce a questo punto l'esigenza di modellare correttamente la rigidezza estensionale delle parti di impalcato interessate da solai rigidi nel proprio piano. Nel programma sono previste le seguenti due differenti possibilità:
1.In ogni solaio di piano, definito a mezzo delle travi perimetrali che lo delimitano, è attivabile l'opzione di inserimento di un elemento finito membranale di arbitrario spessore i cui nodi coincidono con quelli che delimitano il solaio stesso. Lo spessore dell'elemento membranale (privo di peso ed il cui modulo elastico viene assunto automaticamente pari a quello delle travi che lo delimitano) può essere valutato (esternamente al programma) in base alla tipologia del solaio mediante formule di equivalenza del tipo di quella riportata in [11]. Detti elementi membranali non vengono discretizzati al loro interno in quanto ciò che interessa non è stabilire il loro stato di sforzo bensì solo simulare la rigidezza estensionale nel piano del solaio al fine di ottenere più realistici valori degli spostamenti dei nodi così collegati estensionalmente tra loro e delle sollecitazioni nelle aste che in tali nodi convergono.
2.Collegare i nodi delle singole zone rigide dell'impalcato mediante bielle equivalenti tali da collegare i nodi delle stesse zone in modo da contrastarne gli spostamenti relativi nel piano (orizzontale od inclinato) in cui essi sono disposti. Nella figura 4.1 è mostrata la disposizione a croce di tali bielle (in dicate in rosso). La valutazione dell'area equivalente della sezione trasversale delle bielle può essere effettuata (esternamente al programma) sulla base di formule semplificate del tipo di quella riportata in [11]. La definizione della sezione di tali bielle nell'archivio sezioni travi del programma va effettuata selezionando la tipologia sezione generica assegnando cioè non le dimensioni dellla sezione ma direttamente l'area e ponendo quasi nulle le inerzie flettenti e torcente: così facendo si evita l'automatica messa in conto, da parte del programma, del peso proprio della biella sia la necessità di definire, da parte dell'utente, gli svincoli interni dell'asta (implicitamente considerati mediante i valori quasi nulli assegnati ai momenti di inerzia).
Nel caso di impalcati deformabili quindi è necessario considerare nel calcolo tutti i 6 gradi di libertà statici di di ciascun nodo del piano ed anche nell'analisi sismica sarà necessario concentrare le masse di competenza dei singoli nodi del medesimo piano. Allo stesso tempo appare corretto calcolare le travi ricadenti nelle singole zone estensionalmente rigide in presso-tenso flessione retta assumendo nulla la componente della flessione nel piano del solaio (lo sforzo normale viene invece sempre considerato nel calcolo). Ciò oltre a rendere il modello più aderente al reale comportamento consente una semplificazione nel calcolo delle travi e nella loro rappresentazione a mezzo dei consueti esecutivi a "travate".
Il programma consente l'attivazione del calcolo in flessione deviata separatamente per ciascuna trave di piano. All'atto della iniziale definizione dei piani tutte le travi di piano sono considerate solo in flessione retta (opzione di flessione deviata deselezionata). Nel caso di figura 4.1 basterà quindi selezionare la detta opzione solo per le travi 2-5 e 4-7 (di colore blu).
La valutazione della rigidezza membranale dei piani orizzontali va sempre effettuata caso per caso direttamente dal professionista (il programma non svolge automaticamente tale tipo di verifica). In particolare va effettuata separatamente (anche mediante schemi semplificati) la verifica relativa alla capacità degli orizzontamenti di trasmettere le forze, aumentate del 30%, ottenute dall'analisi sismica (§ 7.3.6.1 NTC).
La presenza di zone di impalcato vuote (ad esempio a causa del vano scala o del vano ascensore) può non rappresentare un impedimento all'assunzione dell'ipotesi di piano rigido se dette zone sono vincolate lateralmente (su almeno tre lati) da zone sufficientemente rigide di impalcato.
Maggiore attenzione va prestata se nell'impalcato vi è la presenza contemporanea di pilastri e pareti (§ 1.4) e/o con impalcati allungati in pianta. Nella pianta dell'impalcato di figura 5.1 la presenza di pareti semplici e composte molto rigide rende opportuna una valutazione della rigidezza dell'impalcato che può essere fatta a partire da schemi semplificati come quello di trave continua su appoggi elastici in cui la sezione rettangolare della trave è data dallo spessore del solaio equivalente e dalla larghezza in pianta dell'impalcato, mentre le rigidezze delle molle sono proporzionali alle rigidezza alla traslazione orizzontale delle pareti (pensate isolate). La trave va caricata con un carico distribuito ad esempio uniforme la cui risultante uguaglia la risultante delle forze sismiche al piano. La verifica a resistenza delle sezioni più sollecitate della trave va effettuata amplificando col fattore 1,3 gli sforzi ottenuti (punto 7.3.6.1 NTC).
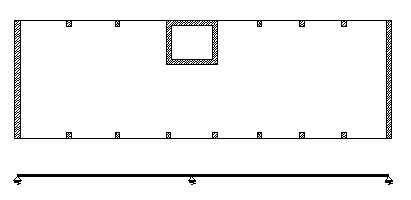
Figura 5.1 - Impalcato allungato con pareti
Nel telaio piano di figura 6.1 le travi del primo e del secondo impalcato orizzontali sono ugualmente comprese in impalcati che, sulla base delle precedenti considerazioni,possono essere considerati rigidi nel proprio piano. Nonostante ciò l'assenza di un pilastro intermedio in copertura rende spingenti le travi inclinate della copertura: se si considera infinitamente rigido il secondo piano non può essere valutato lo sforzo nè lo normale di trazione nelle travi (per ipotesi nullo) nè sopratutto i corretti valori di flessione e sforzo normale nelle travi inclinate. Il secondo impalcato va pertanto assunto come deformabile (pur modellando la rigidezza dei singoli solai dell'impalcato ad esempio con gli elementi finiti membranali di cui sopra). Il nodo di colmo va assegnato come nodo fuori piano o come unico nodo del 3° impalcato, le travi di falda collegando nodi non appartenenti allo stesso piano vanno assegnate come travi fuori piano.
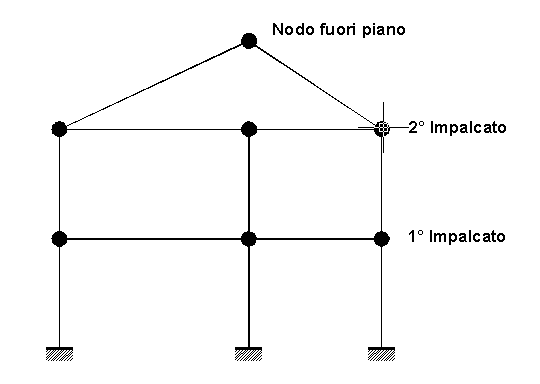
Figura 6.1 - Copertura spingente
Nel caso di impalcato di copertura a falde estensionalmente rigide, con travi non spingenti e con tutti i pilastri di lunghezza finita, tutti i nodi e le travi di detto impalcato risultano essere di piano e pertanto, sia pure in via approssimata, è possibile considerarlo come impalcato rigido con notevole semplificazione nell'input; è questo il caso ad esempio del modello di sinistra rappresentato in Figura 1.1.
In figura 7.1 è mostrato un telaio di un edificio con galleria in cui il primo impalcato è interrotto e pertanto è consentito lo spostamento relativo tra il nodi 1-2 ed i nodi 3-4. Detto impalcato non va pertanto definito come rigido a differenza del secondo che può anche essere definito come rigido.
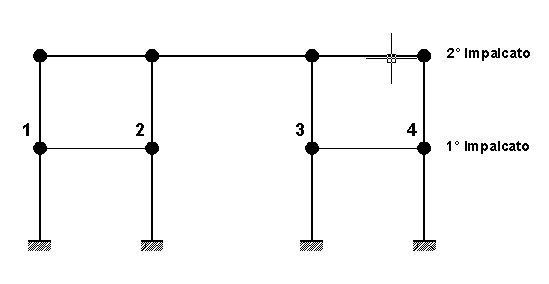
Figura 7.1 - Applicazione errata piano rigido
Il programma consente in uno stesso edificio la presenza contemporanea di piani rigidi e piani deformabili.
|
© GeoStru Software