Un insieme di pareti di forma rettangolare allungata connesse tra loro lungo gli spigoli verticali costituisce una parete composta. In pianta esse assumono forme a U, L, T, E, T doppio etc. In figura 17.1 è rappresentata una parete ad U costituita da una parete d'anima modellata con un elemento monodimensionale (parete) con baricentro sezionale nel nodo B e da due flange anch'esse schematizzate con due pareti nei nodi A e C. Le dimensioni trasversali delle tre pareti possono essere assunte con riferimento ad una delle tre possibili schematizzazioni rappresentate solo planimetricamente in figura: Pianta 1, Pianta 2, Pianta 3. La connessione continua delle pareti lungo gli spigoli viene concentrata solo alla quota dei singoli piani mediante conci (link) rigidi che collegano i baricentri delle pareti agli spigoli. Nell'esempio in fugura 17.1 questo schema è stato realizzato mediante l'introduzione, in corrispondenza di ciascuno dei due impalcati presenti, di due nodi D ed E (posti nei due spigoli di connessione delle pareti) e di 4 aste rigide AD, DB, BE, EC che nel programma vanno assegnate come travi avente un'unica sezione di tipo generico (per dati) a cui vengono assegnati valori elevatissimi ai momenti d'inerzia ed alle aree a taglio e valore quasi nullo al momento d'inerzia polare. Ciò equivale a schematizzare i vincoli nei nodi D ed E di connessione tra le aste rigide come cerniere sferiche. L'ipotesi di conservazione delle sezioni piane viene così rimossa con riferimento all'intera sezione ad U, continuando a valere per le singole pareti semplici le cui rotazioni flessionali nel proprio piano sono però vincolate alla congruenza nei confronti della traslazione verticale (e non alla rotazione torsionale) nei nodi D ed E di continuità. Si viene così a realizzare una comoda schematizzazione del comportamento delle aste composte da pareti sottili, per cui, la torsione viene fronteggiata solo in minima parte dalla rigidezza torsionale alla De Saint Venant delle singole pareti essendo per la maggior parte assorbita dalla rigidezza flessionale delle flange (il cosidetto bimomento della teoria di Vlasov). Anche in assenza di torsione il comportamento flessionale dell'intera parete (per forze orizzontali) così modellata è molto meno rigido di quello che si avrebbe ipotizzando la conservazione della sezione piana per l'intera sezione composta che, in quest'ultimo caso, condurrebbe a sottovalutare gli sforzi nei telai eventualmente presenti nella struttura (ripartizione errata del tagliante di piano).
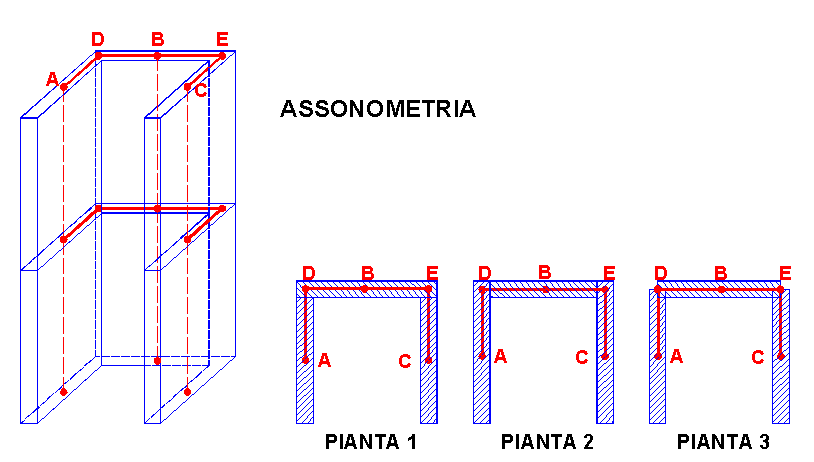
Figura 17.1 - Parete composta ad U
Si sottolinea che i conci rigidi qui introdotti non appartengono alle pareti (come quelli di cui al § 1.4.1 precedente) ma sono vere e proprie travi fittizie che attraverso i nodi ausiliari (del tipo di quelli D ed E in figura 17.1) collegano tra loro i baricentri delle sezioni rettangolari delle pareti (alla quota dei singoli piani).
Le differenze nei risultati del calcolo utilizzando i 3 differenti schemi di suddivisione della sezione trasversale illustrati in figura 17.1 sono relativamente piccole (quanto più lo spessore delle pareti è piccolo) tanto che da un punto di vista pratico risultano più convenienti gli schemi 1 e 2 in quanto le armature finali (ottenute dal programma separatamente per ciascuna parete) non creano problemi di sovrapposizione tra una parete e le altre. Al riguardo le NTC (§ 7.4.4.5.2) prevedono che la verifica di resistenza delle pareti composte vada fatta considerando la parte di sezione costituita dalle anime parallele o approssimativamente parallele alla direzione principale sismica ed attribuendo alle ali dimensioni date dal minimo fra: effettiva larghezza dell'ala, metà della distanza fra anime adiacenti, 25% dell'altezza complessiva della parete hw. Questa semplificazione delle verifiche sezionali da parte delle NTC non ci sembra opportuna nell'ambito della sopraesposta modellazione per i seguenti motivi:
•nel caso di pareti non approssimativamente parallele (ad esempio con inclinazione in pianta di 45°) alle direzioni sismiche non viene fornita alcuna indicazione mentre, avendo qui scomposto la sezione complessiva in sezioni rettangolari, è automatico tener conto delle inclinazioni in pianta delle singole pareti;
•avendo calcolato i momenti flettenti con riferimento alle sezioni rettangolari in una qualsiasi delle modalità illustrate in gigura 17.1 non appare coerente verificare le armature assumendo una sezione più ampia (comprendente ali che si aggiungerebbero alla sezione rettangolare) e quindi con una inerzia flettente maggiore di quella (solo rettangolare) con la quale si sono calcolati gli sforzi flettenti.
Il programma effettua la verifica, coerentemente alle ipotesi assunte, a pressoflessione deviata e taglio delle singole pareti rettangolari ottenute dalla scomposizione della parete composta.
Le aste rigide (link rigidi) non vanno verificate in quanto esprimono solo la voluta congruenza delle deformazioni. E' anche per questo che le relative sezioni vengono assegnate per dati e non per dimensioni (assegnando ad esempio una sezione rettangolare di grandi dimensioni il programma ne calcolerebbe inutilmente le armature ed inoltre, il vincolo di cerniera sferica di estremità andrebbe esplicitato nel vincolamento interno dell'asta).
L'efficacia della modellazione esposta (WCM wide column model) è illustrata nel volume [13] in cui viene svolto, tra l'altro, un confronto, nel complesso soddisfacente, tra i risultati sperimentali e quelli numerici per una parete ad U in campo non lineare. Nonostante lo studio sia recentissimo, per esso non sono stati utilizzati elementi finiti bidimensionali in quanto, in campo non lineare, essi non sono ancora del tutto affidabili e/o maneggiabili con facilità, sia pure in una ricerca sperimentale. Nel citato volume vengono esposti, tra l'altro, i problemi legati alle imprecisioni del modello dovute al fatto che le connessioni (in realtà continue) lungo le pareti sono effettuate solo al livello degli impalcati dei piani con conseguente piccolo errore nei momenti flettenti.
Allo scopo di valutare il modello proposto si consideri la parete composta ad E in figura 18.1 tratta dal manuale di validazione del programma ETABS [12]. Assumendo un modulo elastico E= 3000 ksi = 206843 daN/cm² il carico in sommità F = 100 k = 444482 daN produce i seguenti spostamenti orizzontali e rotazioni intorno all'asse verticale (sempre in sommità):
ETABS |
SAP90 |
Edifici ca |
|
Spost. X (cm) |
0.992 |
0.971 |
0.997 |
Rotaz. Z (rad) |
0.0042 |
0.0043 |
0.0043 |
Risultati che confermano la validità del semplice modello proposto. La simulazione effettuata è descritta nell'esempio 4 del capitolo relativo alla validazione (§ 6.4).
Scematizzando la parete come un'unica asta (stick model) avente la stessa sezione ad E (assegnata come sezione poligonale a 12 vertici) dell'esempio si ottiene per lo spostamento in sommità in direzione X il valore di 0.457 cm cioè meno della metà di quelli sopra riportati. La sopravalutazione della rigidezza è dovuta all'ipotesi di conservazione delle sezioni piane che implica la piena collaborazione delle flange alla rigidezza flessionale sviluppata dalla parete d'anima.
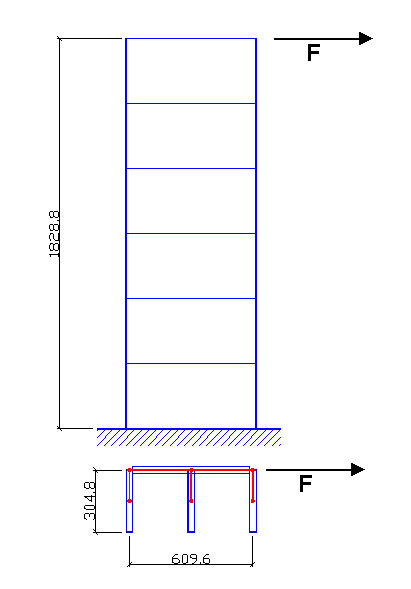
Figura 18.1 - Parete composta ad E
|
© GeoStru Software