Fino ad oggi il calcolo dei pali è stato effettuato sulla base di modelli di interazione palo-terreno di tipo essenzialmente elastico-lineare basati sul continuo elastico omogeneo e sull’interazione alla Winkler con coefficienti di sottofondo eventualmente variabili lungo il fusto del palo per considerare le variazioni stratigrafiche delle caratteristiche geotecniche.
La normativa sismica in vigore (NTC 2018) richiedebbe un calcolo non lineare dell’interazione palo-terreno ("nella caratterizzazione geotecnica è necessario valutare la dipendenza della rigidezza e dello smorzamento dal livello deformativo" § 7.11.2 NTC). Sarebbe inoltre necessaria una valutazione dell’interazione reciproca tra i pali in gruppo (§ 6.4.3 NTC) sottoposti, nel caso sismico, a forze orizzontali dinamiche e cinematiche.
Il calcolo dei pali in gruppo sottoposti ad azioni dinamiche di tipo sismico rappresenta uno dei capitoli più complessi ed ancora non del tutto esplorati dell'analisi strutturale. Non esistono soluzioni generali del problema che possano essere impiegate in un corrente programma di calcolo per uso professionale. Ricerche sono ancora in corso per validare metodologie di calcolo semplificate che evitino il ricorso a metodi generali di soluzione che dovrebbero analizzare la palificata mediante un'analisi dinamica non lineare al passo sotto un accelerogramma di progetto tenendo conto degli effetti dinamici di gruppo, della degradazione ciclica e dell'interazione sia con un terreno stratificato che con la struttura in elevazione. A causa della forte non linearità delle reazioni orizzontali del terreno lungo i pali, l'analisi modale in quanto lineare non è molto coerente. Come pure discutibile risulta l'uso delle impedenze (rigidezze funzione della frequenza espresse mediante numeri in campo complesso) in sostituzione delle rigidezze alla traslazione dei pali.
Una prima semplificazione del problema viene dal § 7.2.6 delle NTC quando a proposito della valutazione dell'interazione dinamica tra fondazione e terreno afferma che è "possibile" (non obbligatorio) "tenere conto della modifica del moto sismico indotta dall'interazione fondazione-terreno. ". Ciò a mezzo di vincoli visco elastici (impedenze dinamiche che tengano conto del livello deformativo....) specie per strutture alte e snelle con effetti del secondo ordine non trascurabili e per strutture fondate su terreno molto deformabili con Vs<100 m/s.
Una prima importante distinzione da fare è quella tra pali isolati e pali in gruppo. Possono considerarsi isolati quei pali disposti in modo che la loro distanza reciproca superi 6÷8 volte il loro diametro (ad esempio pali che portano singolarmente i pilastri e siano collegati da un graticcio di travi o da una platea). I pali che invece sono più vicini della suddetta distanza (detta di estinzione) e che siano tra loro collegati da un unica testata vanno considerati come pali in gruppo (ad esempio ogni plinto su pali realizza un gruppo; come pure una platea su pali ravvicinati).
Per evitare eccessive interazioni e quindi eccessivi cedimenti i pali non devono mai essere a distanza reciproca minore di 3 volte il loro diametro.
Per i pali isolati la resistenza (GEO) assiale e trasversale va calcolata con riferimento ad ognuno di essi, dividendo le resistenze ultime per i fattori di correlazione (§ 6.4.3.1.1, § 6.4.3.1.2). Calcolate così le resistenze caratteristiche queste vanno a loro volta divise per i coefficienti parziali R3 per ottenere le resistenze di progetto con cui verificare singolarmente i pali. Anche i cedimenti dei pali vanno verificati palo per palo (controllando a valle, a cura dell'utente, eventuali cedimenti e rotazioni differenziali).
Per i pali in gruppo le NTC per il calcolo di resistenza GEO per gli SLU/SLV viene richiesto di tener conto delle possibili riduzioni di resistenza per effetto di gruppo. Mettere in conto l'effetto di gruppo consiste in pratica nel valutare (caso per caso) due fattori di efficienza (uno per forze assiale, l'altro per forze trasversali) mediante i quali ridurre la somma delle resistenze complessive dei pali. A tale scopo viene utilizzato un fattore di efficienza Eg tale da ridurre la somma delle resistenze assiali degli n pali in gruppo: Rgruppo = Eg n Rsingolo. La scelta del valore di Egruppo dipende dal numero di pali, dalla geometria del gruppo etc.. Nel caso di terreni incoerenti Egruppo va posto pari ad 1.00. Analogo coefficiente empirico Ggruppo di efficienza va stimato nella verifica a collasso per carichi trasversali sia per terreni coesivi che per terreni incoerenti.
Altra importante norma introdotta dalle NTC 2018 è contenuta nel § 6.4.3.1.1.1:
"Per una palificata, la verifica della condizione [6.2.1] dovrà essere fatta in base alla resistenza caratteristica che risulta dalla somma delle resistenze caratteristiche dei pali che la costituiscono. Sarà comunque necessario valutare possibili riduzioni della resistenza disponibile per effetto di gruppo, tenendo conto della tipologia dei pali, della natura dei terreni interessati e della configurazione geometrica della palificata".
Quindi per pali in gruppo distanti tra loro meno di 6 volte il diametro non andrebbe verificata la resistenza assiale di progetto di ogni palo bensì quella caratteristica somma delle resistenze caratteristiche di tutti i pali del gruppo. Ad avviso di chi scrive l'applicazione di questa norma dovrebbe essere fatta prevedendo un calcolo dei pali assialmente non lineare (la resistenza non deve poter superare quella limite di ogni palo). Di conseguenza (ed in via prudenziale) questo programma in presenza di pali in gruppo (plinti su pali predefiniti e pali tra loro a distanza minore di 6 volte il loro diametro ed indicati nei Dati Generali con il fattore di efficienza Ev<1), continua sì ad effettuare la verifica di resistenza assiale di singolo ogni palo del gruppo, ma lo fa confrontando la forza assiale di combinazione agente sul palo con la resistenza caratteristica e non con la resistenza di progetto (come precedentemente previsto). Per operare questa innovativa verifica l'utente deve assegnare (nell'archivio tipologie pali) al posto della resistenza assiale di progetto quella caratteristica. Naturalmente il programma esegue comunque la verifica di gruppo assiale e trasversale in base ai fattori di efficienza assegnati in input.
Le resistenze di progetto dei pali possono essere calcolate (vedi programmi di servizio) sia a partire da formulazioni analitiche basate sui parametri geotecnici da prove in sito, sia da prove dirette di carico su pali pilota. Per quanto riguarda le verifiche SLE vanno anzitutto inseriti i cedimenti e spostamenti trasversali limite (nell'archivio tipologie pali) dipendenti dai requisiti
Il presente programma può effettuare il calcolo dinamico della sovrastruttura unitamente con la struttura di fondazione (in questo caso con fondazioni su pali) schematizzando le fondazioni stesse come rigidezze prive di massa. Le rigidezze elastiche da assumere per modellare il comportamento terreno vanno ridotte dal progettista in rapporto al livello deformativo atteso.
La modellazione prevista per l'interazione orizzontale pali-terreno è quella elastica lineare alla Winkler.
Pali su suolo elastico alla Winkler
La modellazione per azioni trasversali é prevista alla Winkler anche per terreni stratificati. Essa schematizza il terreno con molle elastiche lineari trasversali (in pratica quasi sempre orizzontali) di intensità variabile da strato a strato e discretizza il palo in conci come esposto nel § 1.10. Ogni palo viene considerato dal programma come una sotto-struttura da assemblare nel sistema risolvente generale dell'intera struttura mediante i valori delle rigidezze del nodo di testa (matrice rigidezze 6x6 corrispondente ai 6 gradi di libertà della testa del palo). Per il calcolo della matrice di rigidezza del palo viene usata la stessa tecnica impiegata per le travi di fondazone su suolo elastico ed illustrata nel § 4.1.
Ogni palo viene considerato dal programma come una sotto-struttura elastica da assemblare nel sistema risolvente generale dell'intera struttura (metodo delle deformazioni) mediante i valori delle rigidezze del nodo di testa (matrice rigidezze 6x6 corrispondente ai 6 gradi di libertà della testa del palo). Ogni palo viene discretizzato in elementi beam nei cui nodi di estremità sono applicate molle lineari trasversali che rappresentano la reazione elastica del terreno ad ogni spostamento trasversale dei nodi delle beam. Dette molle possono assumere rigidezza variabile lungo il fusto in base ai parametri geotecnici assegnati alla tipologia di palo (Archivio tipologie pali) a cui il palo appartiene.
Nel modello di palo con terreno lineare la rigidezza assiale per carico concentrato applicato sulla testa del palo viene determinata con riferimento al grafico di seguito riportato che illustra la relazione di Randolph-Wroth-Fleming (1992): :
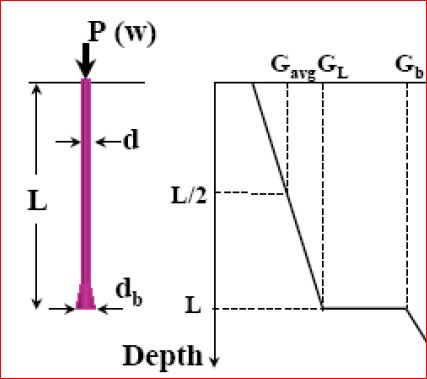
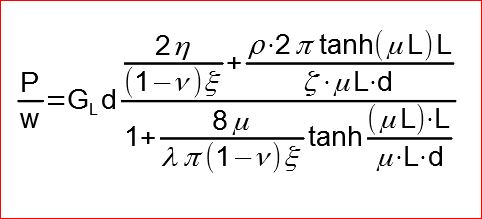
In cui:
η = db / d in questo programma è sempre db = d e quindi η = 1
ξ = GL/ Gb in questo modello è sempre Gb=GL e quindi ξ = 1
ρ = Gavg / GL
λ = Ep /GL con Ep modulo elastico del palo
rm = [0.25 + (0.25 ρ (1-ν) - 0.25) ξ ] L = distanza di estinzione dell'interazione tra pali (detto 'raggio magico')
ζ = ln(2 rm /d)
μ L = 2 (2/(ζλ))0.5 (L/d)
Per applicare la suddetta relazione nel caso di terreno stratificato il valore Gavg viene calcolato come media ponderale dei valori del modulo elastico G lungo il fusto del palo. I valori del modulo elastico G lungo il palo vendono dedotti a partire dai valori Kh delle rigidezze trasversali assegnate lungo il palo mediante la correlazione di Gazetas: Kh= 1.2 Es/d essendo Es il modulo elastico del terreno variabile lungo il palo e d il diametro del palo.
Ogni palo viene discretizzato in conci di trave (elementi beam) aventi lunghezza vicina a quella assegnata (mesh) tra i parametri di calcolo nella finestra dei Dati Generali. In ogni nodo di estremità dei conci viene applicata una molla lineare o non lineare che rappresenta la reazione trasversale del terreno lungo le due metà dei conci a cavallo del nodo. In questo modello lineare la rigidezza delle molle pur variando lungo il palo resta sempre direttamente proporzionale al corrispondente spostamento.
Momenti cinematici
Questi momenti sono prodotti dalla deformazione del terreno in cui sono immersi i pali a seguito del passaggio delle onde sismiche. Le NTC al § 7.11.5.3.2 ne impone la valutazione per costruzioni di classe d'uso III o IV, per terreni di tipo D o peggiori in siti a sismicità media o alta (ag>0.25 g), e, nel caso in cui due strati adiacenti del terreno che circonda i pali presenti un forte contrasto delle rigidezze Gs (rapporto tra i due valori di Gs > 5).
Un calcolo rigoroso di questi momenti presenta notevoli difficoltà e risulta giustificato solo per opere di una certa importanza. Per opere correnti Gazetas (1997) propone una formula semplificata e conservativa con riferimento ad un terreno caratterizzato da due soli strati:
Mmax = 0,042 Ti d³ (L/d)0,3 (Ep/Es)0,65 (Va/Vb)-0,5
con
Ti = As Ro Ha = Tensione tangenziale all'interfaccia
Ro = densità strato superiore
As = accelerazione sismica di progetto alla superficie libera del terreno
Ha = spessore dello strato superiore
Va, Vb = velocità delle onde di taglio dello strato superiore ed inferiore
L, d = lunghezza e diametro del palo
Ep = modulo di Young del palo
Es = modulo elastico del terreno
Verifica sezioni circolari dei pali in c.a.
Viene effettuato il semiprogetto e la verifica della sezione circolare del palo maggiormente sollecitata a flessione come sopra determinata. Nel calcolo di verifica al momento massimo vengono sempre associati i valori dello sforzo normale del taglio e della torsione calcolati nella sezione di attacco del palo.
Nel caso in cui la struttura ricade in zona sismica il punto 7.2.5 delle NTC richiede che i pali restino in campo elastico (come per tutti gli altri tipi di fondazioni) ed abbiano un'area di armatura longitudinale minima pari allo 0.3% di quella del calcestruzzo.
Nel caso di presenza dei momenti cinematici l'armatura massima del palo deve essere estesa a tutta la sua lunghezza.
Il programma progetta e verifica l'armatura necessaria ad assorbire gli sforzi derivanti dalle combinazioni di carico amplificate col fattore di sovraresistenza gRd e dai momenti cinematici eventualmente assegnati.
Può accadere che uno o più pali non siano verificati nei confronti del carico limite per forza orizzontale pur essendo l'armatura ed il conglomerato verificati nei confronti delle massime sollecitazioni calcolate. Se ciò avviene per insufficienza del momento ultimo (ipotesi di palo 'medio' o 'lungo' nella teoria di Broms) si può intervenire nell'archivio sezioni travi/pali (§ 2.2.17) assegnando al numero minimo di barre di armatura della sezione del palo un valore superiore a quello fornito dal calcolo: reiterando il calcolo con armature via via crescenti si può giungere a soddisfare la verifica o si può decidere di modificare il diametro o la disposizione in pianta dei pali.
Calcolo efficienza Ev per carichi assiali nei pali in gruppo
Per pali in gruppo la vigente normativa non sismica (§ 6.4.3 NTC) prescrive la determinazione del carico ultimo complessivo della palificata tenendo conto degli effetti di gruppo. Detto Qult assunto per il carico ultimo del palo singolo il carico ultimo di una palificata comprendente N pali uguali può essere determinato in generale dalla seguente formulazione:
QGult = N Ev Qult
dove Ev è detto il fattore di efficienza della palificata per carichi assiali.
Per terreni incoerenti Ev risulta non minore dell'unità e, cautelativamente, potrà sempre porsi 1. Per terreni coesivi si aggira intorno a 0,6, 0,7 e nel caso di m file di pali con n pali per ogni fila si potrà adottare la seguente formula empirica di Converse Labarre (cfr. [1]):
E = 1 – [2 arctg(i/d)/p ] [(m-1)n +(n-1)m]/ (n m)
dove i è l'interasse tra i pali di diametro d.
Nel caso di piccoli gruppi di pali (caso dei plinti su pali) conviene utilizzare valori predefiniti in base al numero di pali presenti in ogni plinto (metodo di Feld). Valori di riferimento del coefficiente E sono 1.00 per il palo singolo, 0.94 per palo doppio, da 0.82 per 4 pali a 0.72 per 9 pali. Per terreni a grana grossa va sempre assunto E=1.00.
E' sempre consigliabile scegliere un interasse tra i pali superiore a 3 volte il diametro dei pali, oltre che per motivi economici, anche per ridurre gli effetti dell'interazione che si verifica nel comportamento dei pali. Si ricorda che per i pali in gruppo il carico assiale di progetto può essere sostituito da quello caratteristico.
Calcolo efficienza Eh per carichi trasversali nei pali in gruppo
Anche per la determinazione del carico ultimo trasversale complessivo della palificata è necessario mettere in conto degli effetti di gruppo. Detta Hg la forza trasversale di un palo singolo, il valore della forza trasversale totale del gruppo può essere definita dalla seguente formulazione semplificata:
Htot = N Eh Hg
dove Eh è l'efficienza trasversale del gruppo.
Il valore di Eh è sempre inferiore dell'unità e tende all'unità solo per valori di s/d maggiori di 5-6 (s= interasse pali; d = diametro pali). Eh decresce con l'aumentare dello spostamento trascersale, si incrementa se i pali sono meno liberi di ruotare in testa.
E' molto importante aumentare l'interasse s tra i pali per ottenere valori dell'efficienza trasversale prossimi all'unità.
Stante la difficoltà di definire con precisione l'efficienza Eh , anche per la mancanza di estese conferme sperimentali, si consiglia il seguente criterio pratico:
- Per interasse medio tra i pali pari a 3d porre Eh = 0.7.
- Per interasse medio tra i pali pari a 6d porre Eh = 1.0.
- Per interasse medio tra i pali intermedio tra 3d e 6d porre Eh = al valore interpolato tra i due precedenti.
Evitare assolutamente di porre i pali ad interasse < 3d.
|
© GeoStru Software