Allo scopo di fare qualche considerazione sul calcolo delle piastre in c.a. si consideri la piastra quadrata in elevazione in figura semplicemente appoggiata sul contorno e caricata da un carico uniforme di 1000 daN/m².
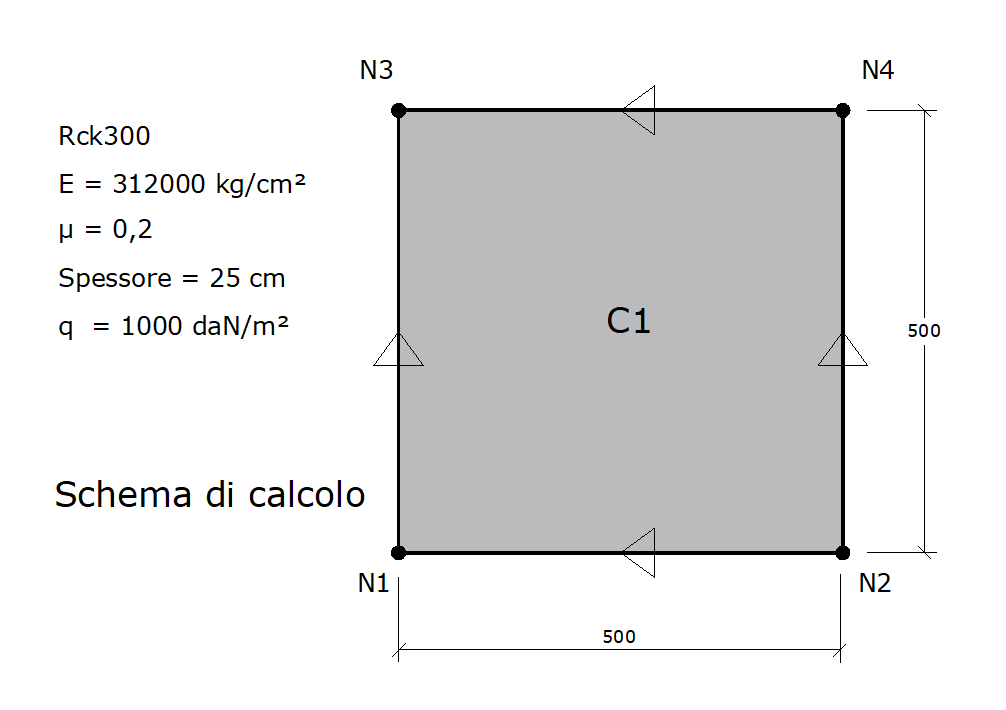
Nell’archivio sezioni campi-platea (§ 2.2.19) si modifica la sezione predefinita precisando lo spessore (25 cm), annullando il valore della costante di Winkler (la piastra è in elevazione) e ponendo la classe del conglomerato pari a quella voluta di Rck300.
Il modello può essere generato dalla finestra dei Dati Generali mediante il modello predefinito di griglia di campi rettangolari.
Il programma però non prevede vincoli continui lungo i lati dei campi di piastra in quanto il programma è orientato al calcolo delle platee su suolo elastico che in genere non prevedono vincoli lungo i bordi. Allo scopo di simulare il vincolo di appoggio su ogni lato del campo è stata inserita una trave di winkler a sezione generica (cioè assegnata per dati) in cui si sono assegnati valori bassissimi ai dati statico-geometrici della sezione ed un valore altissimo al coefficiente di winkler (kw=999999).Il valore assegnato alla larghezza della sezione di contatto trave-terreno è di appena 1 cm per evitare che larghezze maggiori generino momento torcenti sul terreno equivalenti a momenti flettenti negativi lungo i bordi.
Nella tabella campi (§ 2.2.7) si controlla che all’unico campo presente corrisponda il nome della sezione prima modificata e si digita il valore voluto di 1000 daN/m² per il carico uniforme.
Effettuato il calcolo si possono rilevare i seguenti risultati relativi al nodo centrale della piastra (i risultati per ogni nodo risultante dalla discretizzazione compaiono nella finestra di output cliccando col mouse sul nodo voluto dopo aver selezionato la scheda campi platea ):
mx = my = 1115 daNm/m = 1115 daNcm/cm
freccia = 0,050 cm
Per via analitica la teoria classica delle piastre conduce alle seguenti espressioni per le precedenti quantità:
mx = my = 0,03684 (1+m) q L² = 1105 daNm/m
freccia = 0,00406 q L4/B = 0,0599 cm
in cui:
B= E s³ /[12(1- m²)]
E = 312000 daN/cm²
s = 25 cm
m = 0,2
q = 0,1 daN/cm²
L = 500 cm
La soluzione fornita dal programma può quindi ritenersi sufficientemente approssimata a quella esatta.
Ma nel caso di piastre in c.a. è ancora più importante segnalare che a causa della inevitabile fessurazione e dei fenomeni reologici la rigidezza a torsione si riduce molto più sensibilmente di quella a flessione. La conseguente riduzione dell’iperstaticità interna della piastra fornita dalla torsione può essere approssimata dal programma mediante l’assegnazione della percentuale di efficacia del modulo elastico G a torsione nella finestra dei dati generali. Il CEB Model Code 1990 consiglia di assumere come effettiva una percentuale di circa il 10% di G.
Inserendo tale percentuale nei dati di input dell’esempio si ottengono i seguenti nuovi risultati (sempre nel nodo centrale e per m = 0,2):
mx = my = 1810 daNm/m
freccia = 0,079 cm
Si consiglia, pertanto, di effettuare il calcolo delle piastre e delle platee in c.a. (e quindi delle relative armature) con questi ultimi valori di molto superiori (di oltre il 40%) a quelli teorici forniti dalla teoria elastica in quanto maggiormente rispondenti al reale comportamento dei materiali impiegati.
Geostru Software ©