Il modello detto CRSP (Colorado Rockfall Simulation Program) è stato messo a punto da Pfeiffer e Bowen (1989) con lo scopo di modellare il moto di caduta di blocchi aventi la forma di sfere, cilindri o dischi, con sezione circolare nel piano verticale del movimento.
Per descrivere il movimento dei blocchi il modello CRSP applica l'equazione del moto parabolico di un corpo in caduta libera ed il principio di conservazione dell' energia totale.
Il fenomeno dell' impatto viene modellato utilizzando come ulteriori parametri, rispetto al metodo Lumped Mass, la rugosità del pendio e la dimensione dei blocchi.
In particolare il modello CRSP assume che l' angolo formato tra la direzione del blocco ed il profilo del pendio varii secondo una statistica che deve essere definita per ogni caso analizzato. Il modello tratta quindi in modo statistico anche i risultati che principalmente constano nelle velocità e nelle altezze di rimbalzo, rispetto alla superficie del pendio, durante il percorso di caduta. Il modello considera quindi le combinazioni dei movimenti di caduta libera, di rimbalzo, di rotolamento e di scivolamento, che possono variare a seconda delle dimensioni dei blocchi e della rugosità del pendio.
L' affidabilità del modello è stata verificata attraverso confronti tra i risultati numerici e quelli ottenuti da prove in sito.
La descrizione del moto di caduta libera inizia da un punto nel quale, è nota la velocità iniziale scomposta nelle sue componenti orizzontali e verticali. Il blocco è soggetto al movimento di caduta libera fino a quando non collide con la superficie del pendio.
Dall' intersezione vengono ricavate le coordinate del punto di impatto. Il vettore della velocità di pre-impatto V, forma un angolo α con il pendio.
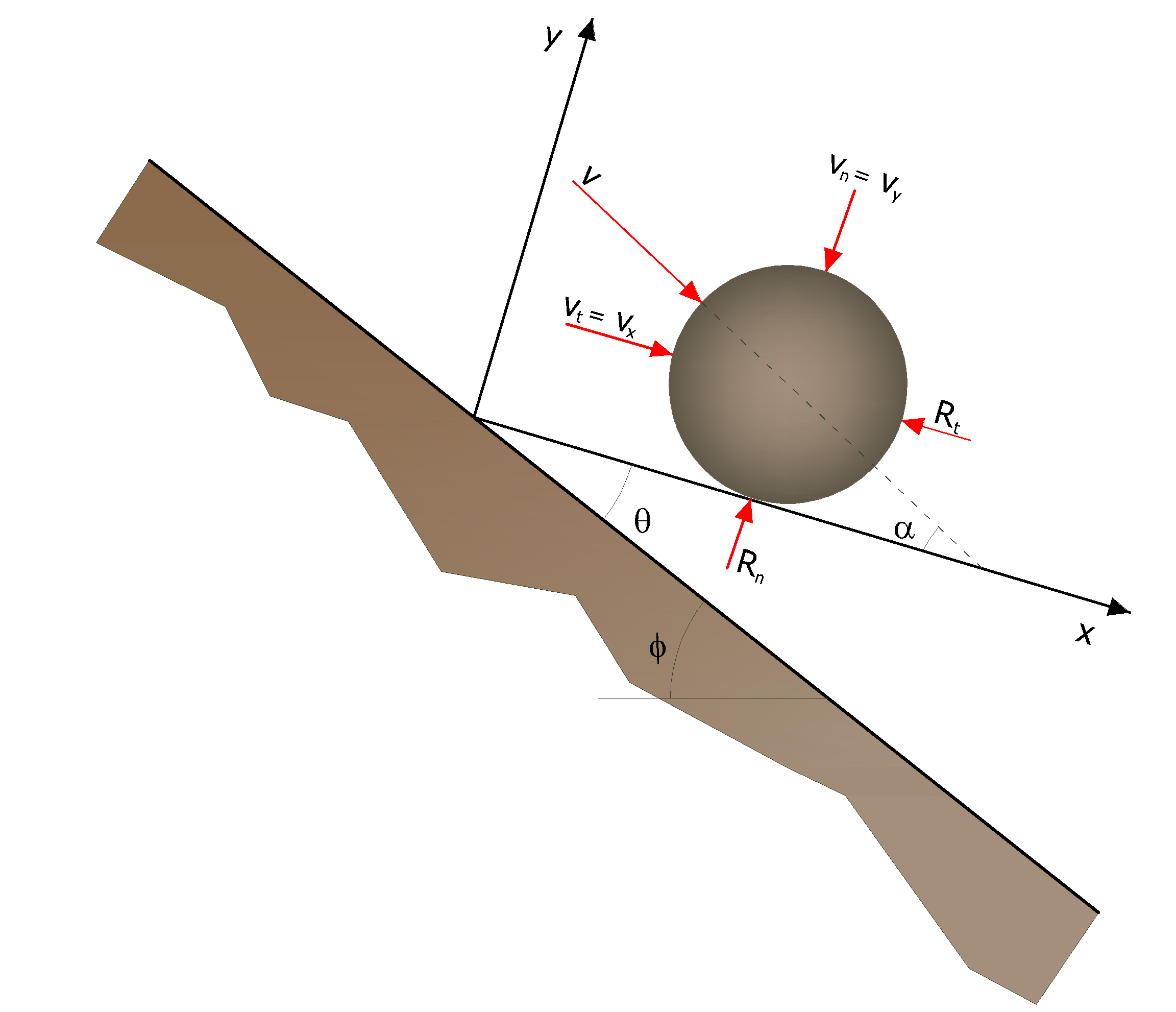
Ad ogni impatto l'inclinazione del pendio φ è fatta variare casualmente in un campo di valori compreso tra 0 e θmax. Il valore di θmax dipende dalla rugosità del pendio e dalla dimensione del blocco e viene determinato da misure in sito. Detto R il raggio del blocco in esame si ha:
![]()
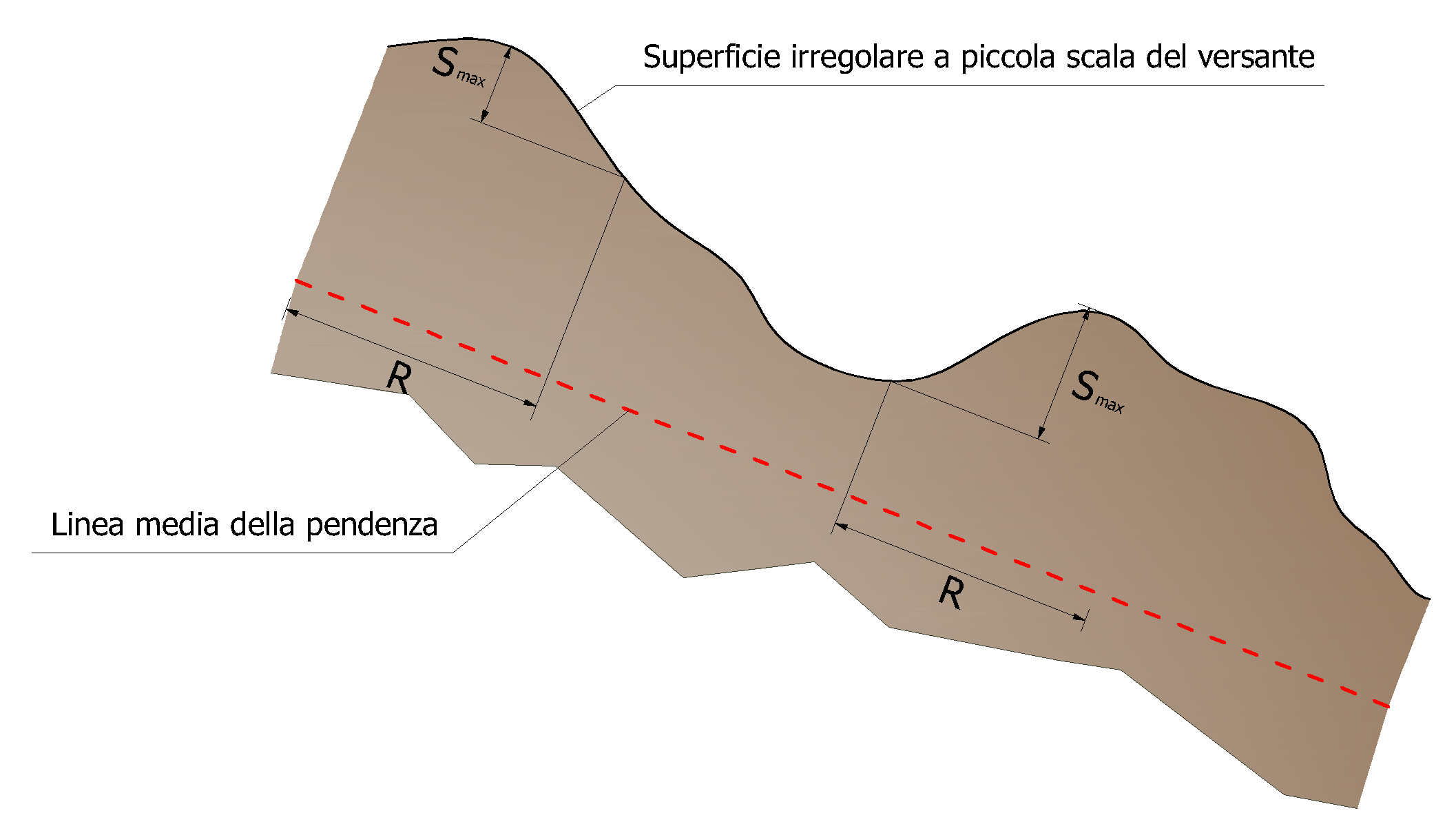
L'angolo θmax è definito come la massima variazione della linea di pendenza media rispetto al raggio R del masso.
La velocità che si ottiene a seguito dell' impatto, viene determinata attraverso l' equazione di conservazione dell' energia totale così espressa:
![]()
dove:
R |
Raggio del blocco; |
M |
Massa del blocco; |
J |
Momento d' inerzia del blocco; |
ω1 |
Velocità angolare prima dell' impatto; |
ω2 |
Velocità angolare dopo l' impatto; |
Vt1 |
Velocità tangenziale prima dell' impatto; |
Vt2 |
Velocità tangenziale dopo l' impatto. |
La funzione f(F) di attrito così definita:
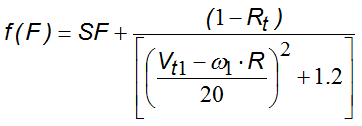
Mentre la funzione di scala SF:
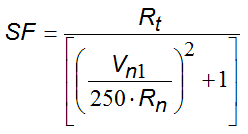
I termini f(F) e SF sono ricavabili attraverso espressioni empiriche che vengono utilizzate per valutare l' energia cinetica dissipata nelle collisioni tra blocco e pendio a causa dell' attrito e dell' urto.
L' attrito riguarda principalmente la dissipazione dell' energia prodotta dalla velocità tangenziale, l' urto quella prodotta dalla velocità normale al pendio.
Le velocità tangenziali e angolari post-collisione sono messe in relazione tra loro dalla seguente equazione:
![]()
che assume che i blocchi abbandonino il contatto con il pendio ruotando, indipendentemente dalla velocità angolare precedente.
La velocità normale post-collisione viene ricavata dalla seguente espressione empirica:
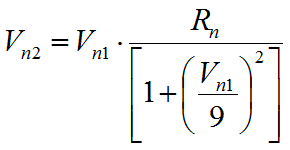
che intende tener conto del fatto, verificato anche sperimentalmente, che il rapporto tra le velocità normali post-impatto e pre-impatto diminuisce con l' aumentare della velocità normale pre-impatto stessa.
Rn |
Coefficienti di restituzione normale; |
Rt |
Coefficienti di restituzione tangenziale; |
R |
Raggio del blocco. |
|
© GEOSTRU- GeoRock 2D