L’introduzione all’analisi di stabilità di pendii naturali parte dal caso semplice di un pendio indefinito, ossia un pendio sufficientemente lungo da essere considerato infinito.
Si consideri un pendio di terreno con c’= 0, inclinato di un angolo β, completamente saturo con filtrazione definita da un angolo α.
L’espressione del fattore di sicurezza F deriva dall’analisi ad equilibrio limite di un blocco di terreno ed assume la seguente forma:
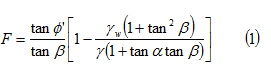
dove F deriva dal rapporto tra la resistenza a taglio disponibile e quella mobilizzata lungo il piano di rottura, γ è il peso di volume del terreno saturo e γw il peso di volume dell’acqua.
Dall’equazione (1) possono essere facilmente ricavati dei casi più semplici di pendio indefinito.
Se il pendio non è saturo, il secondo termine in parentesi quadra dell’equazione si annulla, dando la seguente espressione:
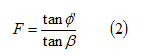
Da cui risulta che un pendio è in condizioni di equilibrio limite (F = 1) quando i suo l’angolo d’inclinazione è uguale all’angolo di resistenza a taglio. L’espressione (2) di F traduce anche la misura di sicurezza per filtrazione verticale (α = 90°).
Mentre per flusso parallelo al pendio (α = β),
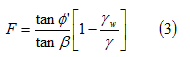
Si noti che in tutte le espressioni di cui sopra il fattore di sicurezza F è indipendente dalla profondità della superficie di rottura.
Quando si considera il caso di filtrazione parallela al pendio, ma con livello dell’acqua al di sotto del profilo del terreno, il fattore di sicurezza si ricava come segue:
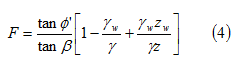
dove zw è la profondità del livello dell’acqua e z è la profondità della superficie di rottura piana.
Un’analisi simile può essere condotta per la stabilità di un pendio indefinito in terreni puramente coesivi, ottenendo:
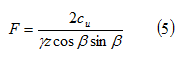
dove cu rappresenta la resistenza a taglio non drenata e γ il peso di volume saturo.
|
© Geostru