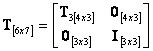<< Click to Display Table of Contents >> Navigation:  Formulation of the beam-column elements > Joining beam-column elements to plane elements. Dissimilar elements. > Beam-column element connected to a plane element

 

The beam-column element stiffness relation is:

 

                                                     

where the displacement and nodal load vectors are:

 

                                   

We assume that the translational displacements at node i of the beam-column element are linearly interpolated along edge 2-3 from translational d.o.f at nodes 2 and 3 of plane element and that rotation θi is the same as the rotation of edge 2-3. In these conditions, between the beam-column displacements and the plane element nodal displacements we can write:

 

                                                                           

where, with , the transformation matrix T is:

 

 

and the displacement vector u contains the displacements of the plane element and displacements at the free node j of the beam-column element:

 

                                             

Applying the principle of virtual displacements if between the displacement u and u’ the relation (107) holds then for the nodal force vectors r we can write a similar relation as:

 

                                                         

We can argue that since r and r’ describe the same resultant force, and the work done by the force during a prescribed virtual displacement must be independent of the coordinate system in which the work is computed. In this conditions, multiply the both terms of eq.(105) with TT and using the equation (107) for displacement vector u’ the equation (105) becomes:

 

                                                           

or in matrix condensed form:

 

                                                             

where the modified stiffness matrix of the beam-column element is:

 

                                   

               

and the modified nodal load vector r is given in equation (111). In this way for the new element the stiffness relation is given by the eq.(113) and the plane element and beam-column element can now be assembled to one another or assembled into the rest of the structure. Node i and its degrees of freedom do not appear in the assembled structures. Node i may be called a “slave” node because its d.o.f. are completely determined by d.o.f. of “master” nodes 2 and 3. Similar relations can be obtained in the case when the beam-column element is mapped in to the higher order plane elements. In this case the nodal displacements of the beam element are quadraticaly interpolated from translational d.o.f of plane element nodes.

 

 

 

 

 

 

 

 

© GeoStru Software