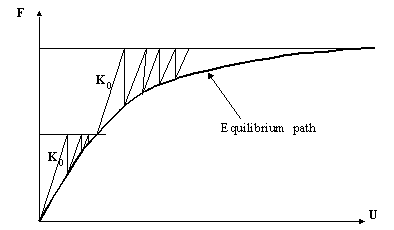
The first approach involves "constant stiffness" iterations in which non-linearity is introduced by iteratively modifying the right hand side "loads" vector. The global stiffness matrix, usually kept elastic, in such an analysis is formed once only. Each iteration thus represents an elastic analysis. Convergence is said to occur when stresses generated by the loads satisfy some stress-strain law or yield or failure criterion within prescribed tolerances. The loads vector at each iteration consists of externally applied loads and self-equilibrating "body loads". The body loads have the effect of redistributing stresses within the system, but they do not alter the net loading on the system. The method is shown in Figure 42. For load-controlled problems, many iterations may be required as failure approached, because the elastic global stiffness matrix starts to seriously overestimate the actual material stiffness.
|
Fig. 42. Constant stiffness method. |
The effects of plastic action are regarded as initial stresses that produce fictious loads, which are combined with the load actually applied. This procedure avoids the expense of repeatedly forming and factoring a tangent-stiffness matrix, but may converge slowly if plastic strains are large or widespread.
|
© GeoStru Software