When the material behavior is nonlinear, material properties in an element are dictated by material properties at a finite number of sampling points in each element. Typically these points are quadrature stations of a numerical integration rule. At each point one must keep a record of strains and update the record in each computational cycle.
The number of points must be small to reduce computational expense. However, to accurately capture the spread of yielding in individual elements many sampling points are needed. The choice is between many simple elements and a smaller number of more sophisticated elements.
|
Fig. 41. Nonlinear analysis procedure |
The implementation of the elasto-plastic constitutive relations in a finite element context requires the consideration of two diferent levels, the global level and the material level respectively. On the global level equilibrium must be satisfied as in any other linear or nonlinear finite element computation, whereas on the material level the plasticity relations must be satisfied. Performing the finite element discretization in the usual way, one ends up with the following equation system:
|
|
(159) |
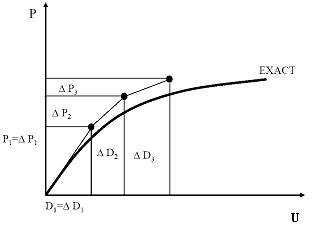
where F represents the applied load vector, U the displacement vector and K the stiffness matrix. Since the stress-strain relation are non-linear, the constitutive matrix depends on current state of stress the stiffness matrix is nonlinear. Two main types of solution procedure can be adopted to model material non-linearity. With either solution method, the load is incremented in several steps and the solution is obtained through a series of linearized steps.
|
© GeoStru Software