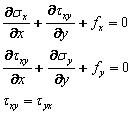<< Click to Display Table of Contents >> Navigation:  Formulation of the element matrices and vectors for elasticity problem > Equilibrium equations

 

Figure 15 shows a plane differential element. The equilibrium equations are developed stating that the differential element is in equilibrium under forces applied to it. Forces come from stresses on the edges and from body forces. In general, stresses and body forces are functions of the coordinates. Thus, for instance, is the rate of change of with respect to x, and is the amount of change of over distance dx.

The stresses in the structure must satisfy the following equilibrium equations:

 

                                                     

where fx and fy are body forces , such as gravity forces, per unit volume. In the finite element method, these equilibrium equations are satisfied in an approximate sense.

 

 

 

 

 

 

 

 

© GeoStru Software