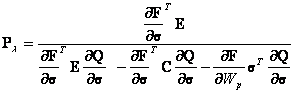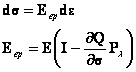<< Click to Display Table of Contents >> Navigation:  Nonlinear analysis formulation > Incremental stress-strain relations

 

We will assume that strain increments include elastic components and plastic components and they are small. An incremental stress-strain relation, analogous to the relation of elasticity can be formulated.

 

During an increment of plastic straining dF=0 thus:

 

 

                               

By substitution:

 

                     

The resulting equation to solve for the plastic multiplier dλ is:

 

                                                     

where Pλ is the row matrix in which both work hardening and strain hardening are included in this expression:

 

                     

Rearranging the terms yield:

 

                                               

where I is a unit matrix and Eep is the generalized tangent constitutive matrix. If Q=F (associated flow rule) this matrix Eep is symmetric. For F<0 (yield has not occur) or F=0 and dF<0 (unloading from plastic state) then Eep=E.

The tangent stiffness matrix kt is now given by:

 

 

 

 

 

 

 

 

 

© GeoStru Software