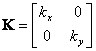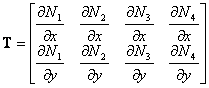<< Click to Display Table of Contents >> Navigation:  »No topics above this level« Steady state analysis

 

The gouverning partial differential equation for a confined aquifier with flow in the horizontal (x,y) plane is:

 

                               

Where ϕ is the fluid potential or total head measured from the bottom of the aquifier, kx and ky are the coefficients of the permeability in the x and y directions and Q is the recharge. Pumping is a negative Q. The finite element discretization process reduces the differential equation to a set of equilibrium type equations of the form:

 

                                             

Where kc is the symmetrical conductivity matrix, Φ is a vector of nodal potential (total head) values, and q is a vector of nodal inflows/outflows. The element matrices are calculated using:

 

                             

Assuming that the principal axes of the permeability tensor coincide with x and y, the property matrix K is:

 

                                               

and the T matrix is similar with the strain-displacement matrix B in the stress analysis. For instance for 4 noded quadrilateral element the matrix T is given by:

 

 

 

 

 

 

 

 

 

 

© GeoStru Software