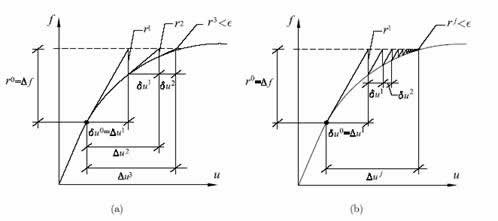
Loads F on the structure are applied in increments ΔF1, ΔF2, and so on, so that 
. The graphical interpretation of the method for a problem with one displacement variable is shown in Figure 45 where the subscripts i indicating the load step number have been dropped. Procedural steps are outlined as follows.
1. For the first computational cycle (i=1) assume Eep =E for all elements. Apply the first load increment ΔF1.
2. Using the current strains, determine the current Eep in each element. Obtain the 
for each element. Determine the residual force if any. Obtain the current structure (global) tangent stiffness Kt,i and solve 
. From 
obtain the current strain increment 
for each element.
3. If any element makes the elasto to plastic transition revise Eep return to previous step 2 and repeat the steps 2 and 3 until convergence.
4. Update the displacement vector
, the strains 
and the stress 
.
5. Apply the next load increment and return to step 2.
6. Stop when sum of incremental loads equals the total load or the structure collapse.
|
Fig. 45. Solution procedure (a) Full Newton-Raphson procedure (b) Modified Newton-Raphson procedure. |
Usually the so-called modified Newton-Raphson method is used. The modification consists of computing the tangent stiffness only once in the beginning of each load step rather than in each iteration as shown in Figure 45(b). Therefore, in step 2 of the above algorithm the tangent stiffness matrix is formed and factorized only once at the beginning of the load increment.
During the iteration process the residual forces are computed. Convergence is said to have occurred, if the absolute change in all components of residual force vector, as a fraction of the maximum absolute component of force vector is less than a predefined tolerance.
|
© GeoStru Software