<< Click to Display Table of Contents >> Navigation:  Nonlinear analysis formulation > Elastic-plastic procedures > Tangent (variable)-stiffness method > Integration of the constitutive relations. Consistent tangent matrix

 

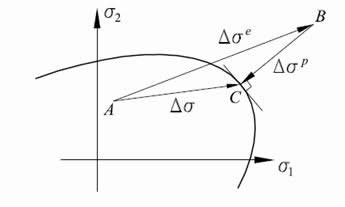
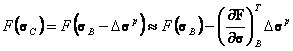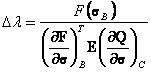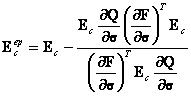Referring to Figure 44 from a point A lying inside or on the yield surface an elastic predictor is applied. This leads to a state of stress outside the yield surface, increments end up at point B. To fulfill the yield condition a plastic corrector is applied, thus returning the stresses to the yield surface at point C. The plastic corrector is determined by two quantities, the scalar Δλ giving the magnitude, and the gradient of the loading surface giving the direction. The magnitude Δλ is determined such that the yield condition is fulfilled:

 

                                           

where is given by

 

                                     

 

 

 

 

A first order Taylor expansion of the yield function at B gives:

 

                                 

Inserting the expression for into the above relation and enforcing consistency of the yield function at point C gives a step size of:

 

                                               

 

With the backward Euler integration scheme, a consistent tangent modular matrix can be formed.

 

                     

On differentiation we get:

 

 

                                       

where is known as the "consistent tangent matrix and is given by:

 

                                               

and

 

 

 

 

 

 

 

 

 

 

© GeoStru Software