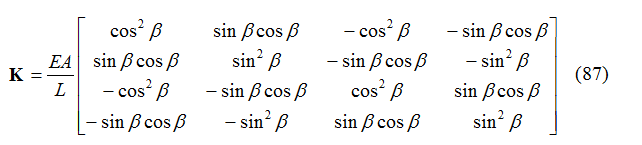La Figura 27 mostra una barra rettilinea in cui i gradi di libertà ai nodi sono gli spostamenti assiali e trasversali (ui, vi, uj, vj).
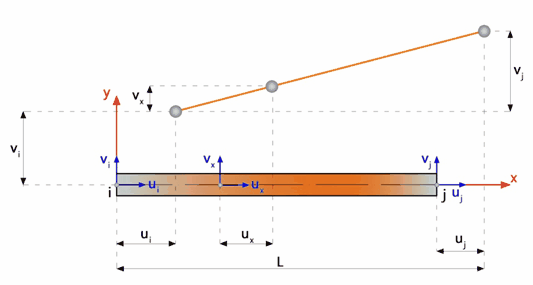
Figura 27. Chiodo.
Un campo degli spostamenti lineare è un’approssimazione appropriata:

Imponendo le condizioni limite, il campo degli spostamenti può essere riscritto come:
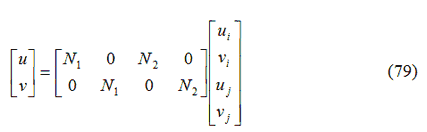
dove le funzioni di forma Ni sono:

In cui ![]()
La deformazione assiale dell’elemento è definita come:
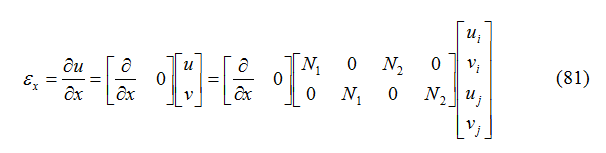
Oppure, in forma compatta, la relazione che intercorre tra gli spostamenti e le deformazioni può essere espressa come:

dove:
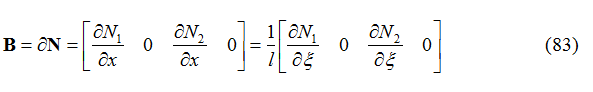
e rappresenta l’operatore deformazione-spostamento.
La matrice delle rigidezze dell’elemento è calcolata in questo caso come:
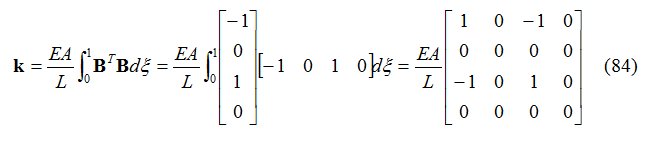
dove EA rappresenta la rigidezza assiale dell’elemento, E è il modulo di Young, A l’area della sezione trasversale e L la lunghezza dell’elemento.
La matrice delle rigidezze k sopra definita mette in relazione le forze assiali con gli spostamenti assiali valutati entrambe ai nodi, e rappresenta la matrice delle rigidezze nel sistema di riferimento locale (degli elementi). Se la barra è orientata con un angolo di inclinazione β nel piano xy, la matrice può essere trasformata utilizzando una matrice di rotazione:
![]()
dove, per il piano xy, la matrice di rotazione è definita come:
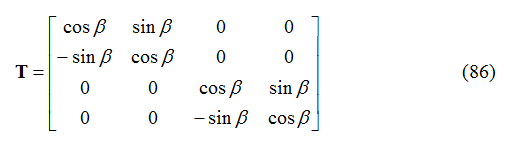
La matrice delle rigidezze nelle coordinate globali del sistema diventa quindi: