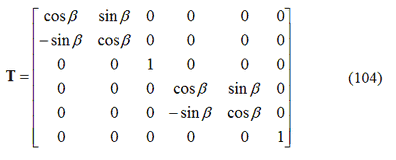La Figura 28 mostra i sei gradi di libertà di un elemento rettilineo trave-pilastro. La rotazione θ si assume talmente piccola che ![]() .
.
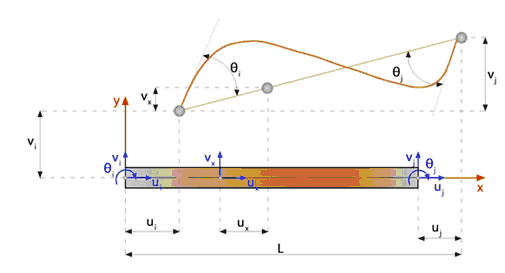
Fig. 28.Elemento trave-pilastro.
Il campo degli spostamenti lungo l’elemento si assume avente la seguente forma:
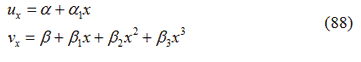
Si utilizza quindi una forma lineare per gli spostamenti assiali e un polinomio di terzo grado per gli spostamenti trasversali: la forma polinomiale di terzo grado è stata scelta per gli spostamenti trasversali poiché, per un elemento caricato soltanto nodi, le forze di taglio e la variazione del momento flettente lungo l’elemento sono costanti e lineari. Infatti:
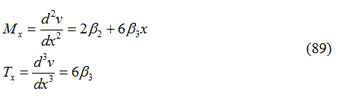
Imponendo le condizioni limite il campo degli spostamenti dell’elemento può essere riscritto come:
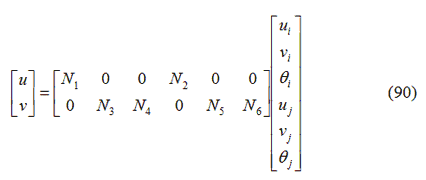
dove le funzioni di forma Ni in questo caso sono definite come:
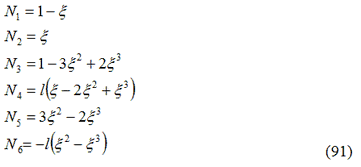
In cui ![]() .
.
Assumendo una distribuzione lineare delle deformazioni lungo la sezione trasversale (Ipotesi di sezione piana) la relazione tra deformazioni e spostamenti è:

Che può essere riscritta in forma matriciale come:
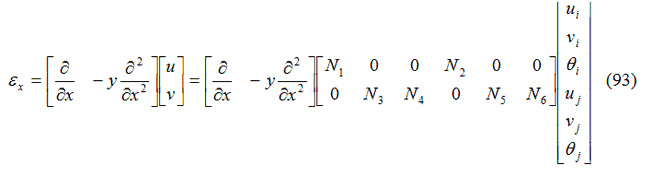
Oppure, in forma compatta:
![]()
Dove u rappresenta il vettore spostamento nodale e B rappresenta l’operatore deformazione-spostamento:
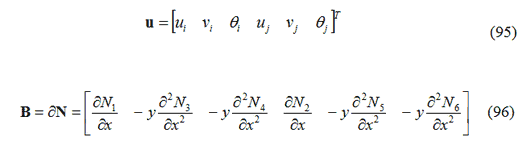
Oppure con le seguenti relazioni:

Assumendo una sezione piana doppiamente simmetrica, la matrice delle rigidezze dell’elemento può essere calcolata come:
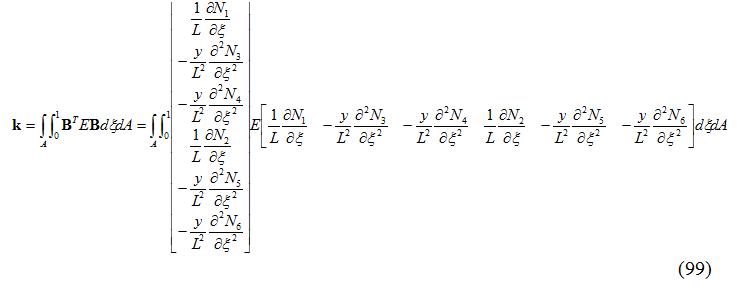
In cui sono definiti il momento di inerzia I e l’area della sezione trasversale A:

Per valori costanti del prodotto EI, la matrice delle rigidezze dell’elemento è data dall’Equazione (99):
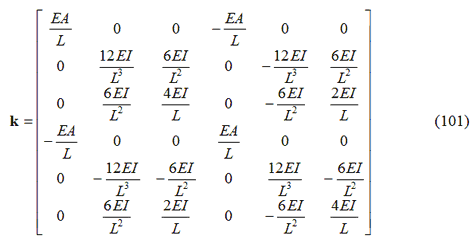
Una leggera modifica all’Equazione 101 consente di tener conto della deformazione trasversale di taglio (Trave di Timoshenko), in modo da ottenere:
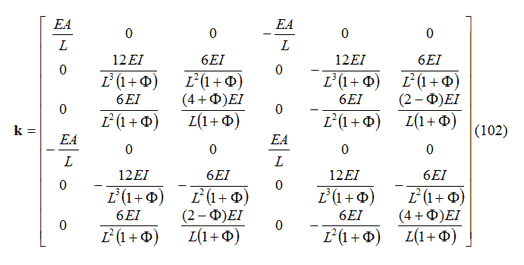
dove ![]() , in cui G rappresenta il modulo di taglio, As la sezione di taglio e il prodotto GAs rappresenta la rigidezza al taglio.
, in cui G rappresenta il modulo di taglio, As la sezione di taglio e il prodotto GAs rappresenta la rigidezza al taglio.
Se la trave è inclinata di un angolo β rispetto all’asse X delle coordinate globali, la matrice delle rigidezze dell’elemento, nel sistema di coordinate globali, è definita come:
![]()
dove la matrice di rotazione T ha la seguente espressione: