Si consideri un corpo elastico lineare soggetto ad un sistema di forze conservative. Sia V il suo volume ed S la sua superficie, allora il funzionale Energia Potenziale Totale si ottiene sottraendo dall’energia di deformazione del mezzo il lavoro delle forze applicate ovvero:
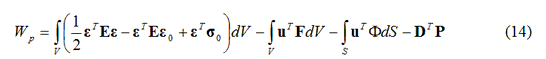

Gli spostamenti nodali si ottengono interpolando i gradi di libertà degli elementi, contenuti nel vettore d, attraverso la matrice delle funzioni di forma N:
![]()
Le deformazioni si ottengono dagli spostamenti tramite differenzazione.
![]()
dove:
![]()
e rappresenta l’operatore deformazione-spostamento.
La matrice operatore differenziale ![]() è definita, nel caso di problemi piani, come:
è definita, nel caso di problemi piani, come:

Sostituendo all’Equazione 14 le espressioni di u e di ε, si ricava:
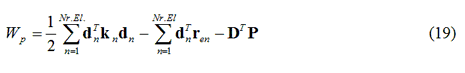
dove la sommatoria include tutti i contributi provenienti dagli elementi finiti della struttura.
Gli elementi della matrice delle rigidezze e gli elementi equivalenti del vettore dei carichi nodali sono definiti come:

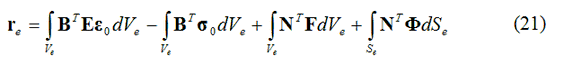
dove Ve ed Se rappresentano rispettivamente il volume e la superficie di un singolo elemento.
Sostituendo nell’Equazione 14 al vettore d il vettore D, contenente i gradi di libertà strutturali globali, l’Equazione 14 si trasforma come segue:
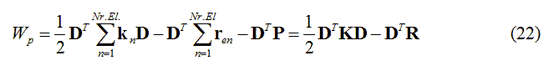
Con:

dove K rappresenta la matrice delle rigidezze globale ed R il vettore delle forze nodali espresse nelle coordinate globali.
Nell’Equazione 22 la sommatoria indica l’assemblaggio degli elementi della matrice e dei vettori. In questo modo il funzionale Energia Potenziale Totale Wp dipende dai gradi di libertà D e gode della proprietà di stazionarietà:

O in maniera esplicita:

ottenendo le equazioni algebriche simultanee da risolvere per le n incognite che rappresentano gli spostamenti associati ad ogni grado di libertà componente il vettore D.
Pertanto:
![]()
Dove K e R rappresentano rispettivamente la matrice delle rigidezze globale e il vettore dei carichi nodali assemblati per l’intera struttura.