Principalele definitii privind analiza probabilisticã a mãrimilor hidrologice cu referire la modelul TCEV sunt reproduse mai jos:
Calcul punctual
Calculul xT al valorii luate de mãrimea hidrologicã în corespondentã cu o perioadã de întoarcere asignatã pe baza seriei esantion a variabilei x în punctul de interax.
Calcul regional
Calculul xT al valorii luate de mãrimea hidrologicã în corespondentã cu o perioadã de întoarcere asignatã utilizãnd informatia furnizatã de serii istorice disponibile în regiunea în care se gãseste punctul de interax.
Calcul mixt
Calculul xT al valorii luate de mãrimea hidrologicã în corespondentã cu o preioadã de întoarcere obtinut combinând informatia punctualã si cea regionalã.
Modelul probabilistic TCEV (two component extreme value) (1)
Modelul cu dublã componentã TCEV presupune cã valorile extreme ale unei mãrimi hidrologice (debit, ploaie) fac parte din douã populatii diferite legate de diverse fenimene meteorologice.
La baza acestei ipoteze stã faptul cã multe serii de maxime anuale prezintã una sau mai multe valori considerabil mai mari decât altele astfel încât par sã nu provinã de la aceeasi populatie ca si celelalte date.
Expresia CDF a distributiei TCEV este datã de:
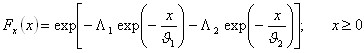
În expresia precedentã sunt indicati cu indice 1 parametrii ce privesc "componenta bazã" si cu indice 2 parametrii privind "componenta extraordinarã".
Parametrii Λ1 si Λ2 reprezintã numãrul mediu anual de evenimente independente a celor douã componente, în timp ce ϑ1 si ϑ2 exprimã valoarea lor medie anualã.
Distributia TCEV echivalentã produsului celor douã distributii ale lui Gumbel, cu care coincide, se ia Λ2=0.
Fãcând referire la variabila standardizatã:
![]()
avem CDF de y este dat de:
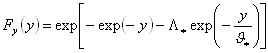
având loc:
![]()
Media distributiei TCEV este datã de expresia:
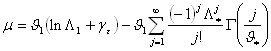
cu γε=0,5772, constanta lui Eulero. Cu simbolul Γ este indicatã functia gamma:
![]()
Coeficientul de variatie reoretic depinde de Λ1, Λ* si ϑ* si este deci independent de ϑ1.
Coeficientul de asimetrie teoretic depinde de Λ* si ϑ* si este deci independent de Λ1 si ϑ1.
Distributia probabilisticã TCEV: Modele regionale
Modelul TCEV permite construirea unui model regional articulat într-o structurã ierarhicã.
Se poate presupune cã existã regiuni în care este constant doar coeficientul de asimetrie si deci sunt constanti parametrii Λ* si ϑ* si subregiuni ale acestora, mai limitate, în care este constant si coeficientul de variatie si, deci, si parametrul Λ1.
Primul nivel de regionalizare constã în identificarea zonelor omogene (ZO) în care se poate considera cã, coeficientul de asimetrie teoretic al seriilor maximelor anuale este constant. Parametrii Λ* si ϑ* pot fi calculati utilizând toate seriile istorice disponibile în zonã, reducând în mod considerabil incertitudinea estimãrii.
La al doilea nivel de regionalizare se identificã subzone omogene (SZO), cu extensie mai micã decât cele precedente, în care pe lângã coeficientul de asimetrie este constant si coeficientul de variatie. Într-o subzonã sunt constanti deci constanti cei trei parametrii Λ1, Λ* si ϑ*. Λ1 poate fi deci calculat pe baza tuturor seriilor istorice din subzonã.
Într-o subzonã rãmâne constant CDF al x/μ. Din expresia CDF a TCEV, introducând parametrii Λ* si ϑ* avem:
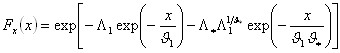
putem scrie:
![]()
adicã:
![]()
luând
![]()
si
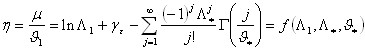
se obtine:
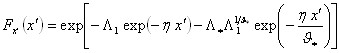
cãreia i se dã denumirea de curbã de crestere.
La al treilea nivel de regionalizare se identificã în interiorul subzonei omogene relatiile care existã între μ si caracteristicile fizice sau climatice ale bazinelor.
Calculul xT al unei mãrimi hidrologice la un timp de întoarcere orefixat poate fi efectuat, pe baza modelului TCEV, în patru moduri diverse:
a) |
La nivel de regionalizare zero, în care toti parametrii modelului sunt calculati de la o singurã serie |
b) |
La nivel de regionalizare unu, în care parametrii Λ* si ϑ* sunt calculati la nivel regional iar Λ1 si ϑ1 de la o singurã serie |
c) |
La nivel de regionalizare doi, în care parametrii Λ*, ϑ* si Λ1 sunt calculati la nivel regional iar ϑ1 de la o singurã serie |
d) |
La nivel de regionalizare trei, în care parametrii sunt calculati cu tehnici de analizã regionalã |
© 2020 GeoStru Software