It is customary in the design practice to evaluate the pressures acting on the soil by adopting an approach "borrowed" from structural mechanics, considering the section sets of the foundation as presso-inflessa.
The calculation of the design pressure is performed considering the section partially reactant and with triangular distribution of the pressures on the soil.
The general case is that of a solid of De Saint Venant urged to normal eccentric stress, when the resultant of the external forces acting on the free base, is reduced to a normal stress N and a bending moment M.
This type of system is statically equivalent to a force N directed along the axis of the solid, applied at a point C, called the center of stress, different from the center of gravity G of the section partially reactant.
The joining CG provides the direction of the axis of the stress, together with that of the neutral axis defined as the anti polar of the center C of stress compared to the central inertia ellipse of the reactant section.
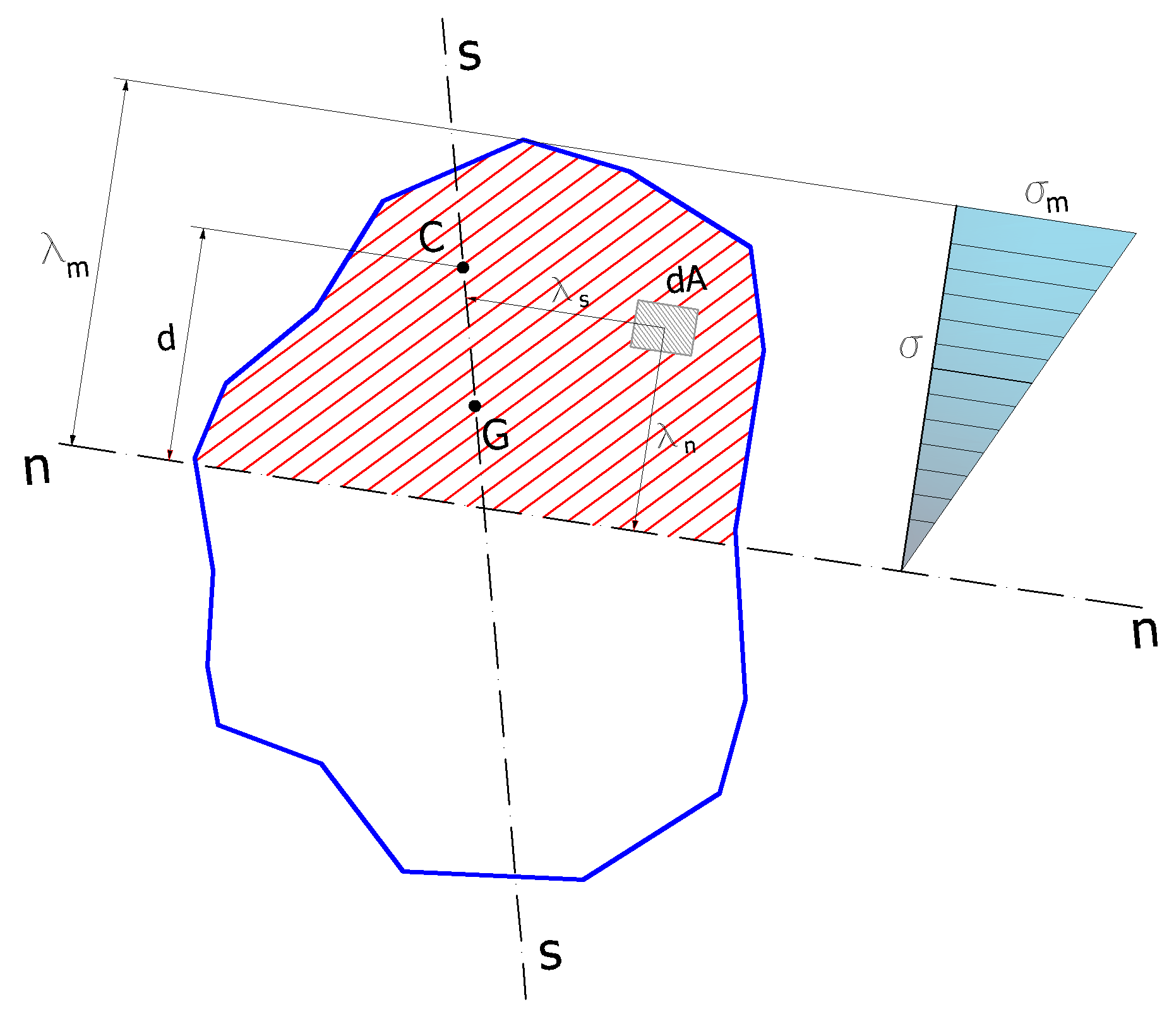
The unknowns of the problem, in the hypothesis of validity of the principle of conservation of plane sections and validity of Hooke's law, are three:
•two fix the position of the neutral axis
•another unknown variable is represented by the value of the stress in a generic point of the section
The solution of the problem is reached through a system of three equations:
1.Translation equilibrium equation in the direction normal to the section:
![]()
2.Rotation equilibrium equation with respect to the neutral axis:
![]()
3.Rotation equilibrium equation with respect to the stress axis:
![]()
From the starting assumptions we can write the following relationship:

Substituting the above equation into the three equilibrium equations, we obtain:

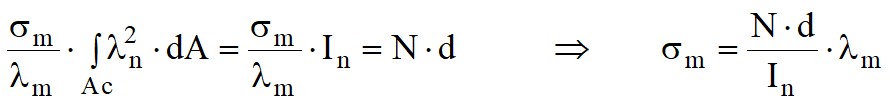
having denoted by Sn the static moment of the reactant area with respect to the neutral axis and by In the moment of inertia of the reactant section with respect to the neutral axis or by the combination of the two results we obtain the position of the neutral axis:

Finally, from the rotation equilibrium equation with respect to the stress axis we obtain a relationship that expresses the condition that:
"the neutral axis and the stress axis are conjugated with respect to the inertia ellipse of the reacting section"
![]()
Known the position of the neutral axis we can calculate the stress at any point on the reacting section.
© GeoStru