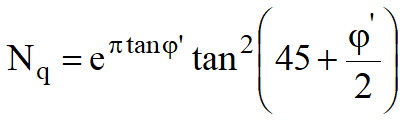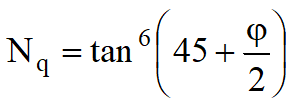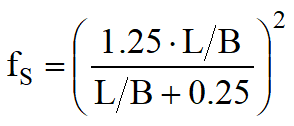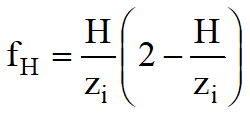Il carico limite di una fondazione superficiale può essere definito con riferimento a quel valore massimo del carico per il quale in nessun punto del sottosuolo si raggiunge la condizione di rottura (metodo di Frohlich), oppure con riferimento a quel valore del carico, maggiore del precedente, per il quale il fenomeno di rottura si è esteso ad un ampio volume del suolo (metodo di Prandtl e successivi).
Osservazioni sperimentali hanno dimostrato che il terreno può arrivare a rottura attraverso tre meccanismi (vedi Figura seguente):
La rottura generale è caratterizzata dalla formazione di superfici di scorrimento ben definite che parte della fondazione e raggiunge il piano di campagna, e da un rigonfiamento del terreno ai lati della fondazione.
La rottura per punzonamento in cui l'affondamento della fondazione è reso possibile dalla formazione di piani di taglio verticali, lungo il perimetro, senza generare superfici di scorrimento.
La rottura locale, corrisponde al formarsi ancora di una chiara superficie di scorrimento al di sotto della fondazione, che tuttavia si disperde nel terreno adiacente, si evidenzia una timida tendenza al rigonfiamento laterale del terreno.
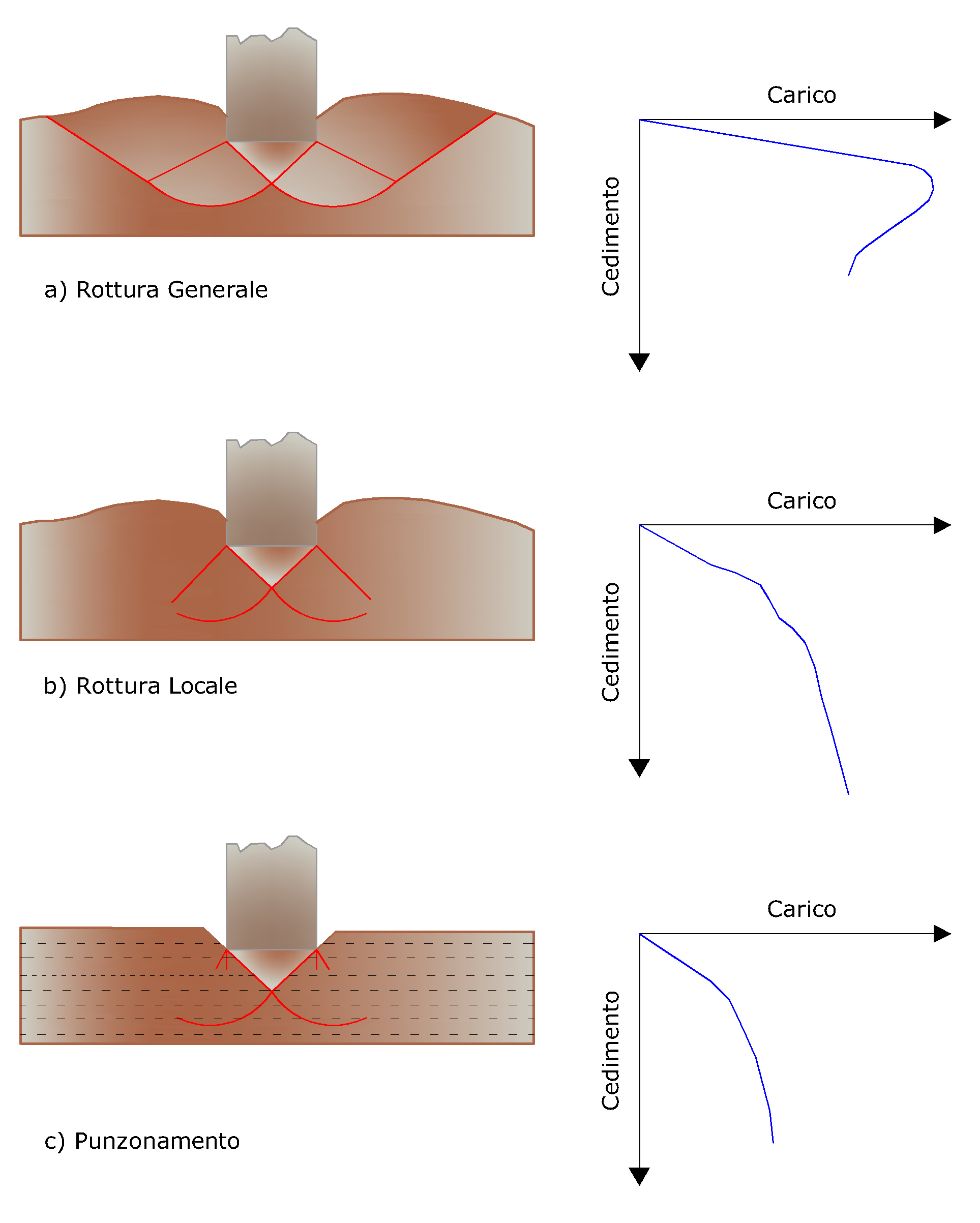
Tipi di rottura del terreno
Le soluzioni disponibili per il calcolo del carico limite sono basate sull'assunzione del comportamento del terreno rigido-plastico e sono perciò, a stretto rigore, applicabili solo al caso di rottura generale.
Si può dimostrare che il carico limite di un terreno è la somma di tre fattori: peso del terreno γ', sovraccarico q' e coesione c'; le soluzioni oggi disponibili sono state ricavate dalla sovrapposizione di singoli problemi indipendenti .
Prandtl (1921) ha studiato il problema della rottura di un semispazio elastico per effetto di un carico applicato sulla sua superficie con riferimento all'acciaio, caratterizzando la resistenza a rottura con una legge del tipo:
![]()
valida anche per i terreni.
Le ipotesi e le condizioni introdotte da Prandtl sono le seguenti:
•Comportamento rigido - plastico.
•Resistenza a rottura del materiale esprimibile con la relazione (1-1).
•Carico uniforme, verticale ed applicato su una striscia di lunghezza infinita e di larghezza 2b (stato di deformazione piana).
•Tensioni tangenziali nulle al contatto fra la striscia di carico e la superficie limite del semispazio.
•Assenza di sovraccarico ai bordi della fondazione (q'=0).
All'atto della rottura si verifica la plasticizzazione del materiale racchiuso fra la superficie limite del semispazio e la superficie GFBCD (vedi Figura). Nel triangolo AEB la rottura avviene secondo due famiglie di segmenti rettilinei ed inclinati di 45°+φ/2 rispetto all'orizzontale.
Nelle zone ABF e EBC la rottura si produce lungo due famiglie di linee, l'una costituita da segmenti rettilinei passanti rispettivamente per i punti A ed E e l'altra da archi di spirali logaritmiche. I poli di queste sono i punti A ed E.
Nei triangoli AFG e ECD la rottura avviene su segmenti inclinati di ±(45°+φ/2 ) rispetto alla verticale.
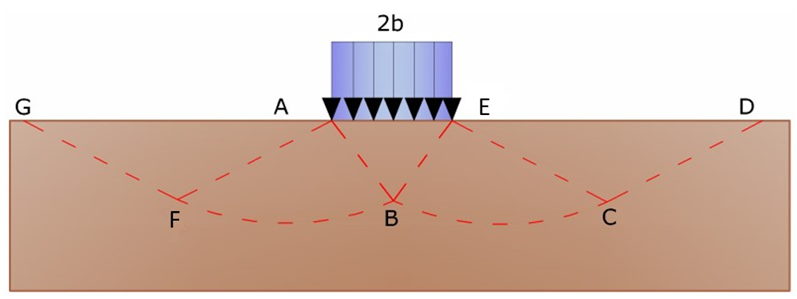
Soluzione di Prandl
Individuato così il volume di terreno portato a rottura dal carico limite, questo può essere calcolato scrivendo la condizione di equilibrio fra le forze agenti su qualsiasi volume di terreno delimitato in basso da una qualunque delle superfici di scorrimento. Si arriva quindi alla soluzione esatta esprimibile nella forma:
![]()
dove il coefficiente B dipende soltanto dall'angolo di attrito j' del terreno. Per φ'≠0 il fattore B= 5,14.
Nel caso particolare di terreno privo di coesione (c'=0, γ'≠0) risulta q'=0, secondo la teoria di Prandl, non sarebbe dunque possibile applicare nessun carico ad sulla superficie limite di un terreno incoerente.
Questa teoria, anche se non applicabile praticamente, ha dato inizio a tutte le ricerche ed i metodi di calcolo successivi.
Infatti Caquot si pose nelle stesse condizioni di Prandtl ad eccezione del fatto che la striscia di carico non è più applicata sulla superficie limite del semispazio, ma ad una profondità h, con h<2b; il terreno compreso tra la superficie e la profondità h ha le seguenti caratteristiche: γ'=0, φ'≠0, c'=0, rappresenta un mezzo dotato di peso ma privo di resistenza. Risolvendo le equazioni di equilibrio si arriva all'equazione esatta:
![]()
che sicuramente è un passo avanti rispetto a Prandtl, ma che ancora non rispecchia la realtà.
Terzaghi (1955)
Terzaghi, proseguendo lo studio di Caquot, ha apportato alcune modifiche per tenere conto delle effettive caratteristiche dell'insieme opera di fondazione-terreno. Sotto l'azione del carico trasmesso dalla fondazione il terreno che si trova a contatto con la fondazione stessa tende a sfuggire lateralmente, ma ne è impedito dalle resistenze tangenziali che si sviluppano fra la fondazione ed il terreno. Ciò comporta una modifica dello stato tensionale nel terreno posto direttamente al di sotto della fondazione; per tenerne conto Terzaghi assegna ai lati AB ed EB del cuneo di Prandtl una inclinazione Y rispetto all'orizzontale, scegliendo il valore di Y in funzione delle caratteristiche meccaniche del terreno al contatto terreno-opera di fondazione.
L'ipotesi γ' =0 per il terreno sotto la fondazione viene così superata ammettendo che le superfici di rottura restino inalterate, l'espressione del carico limite è quindi:
![]()
in cui:
C è un coefficiente che risulta funzione dell'angolo di attrito j del terreno posto al di sotto del piano di posa e dell'angolo j prima definito;
b è la semilarghezza della striscia.
Inoltre, basandosi su dati sperimentali, Terzaghi passa dal problema piano al problema spaziale introducendo dei fattori di forma.
Un ulteriore contributo è stato apportato da Terzaghi sull'effettivo comportamento del terreno.
Nel metodo di Prandtl si ipotizza un comportamento del terreno rigido-plastico, Terzaghi invece ammette questo comportamento nei terreni molto compatti.
In essi, infatti, la curva carichi-cedimenti presenta un primo tratto rettilineo, seguito da un breve tratto curvilineo (comportamento elasto-plastico); la rottura è istantanea ed il valore del carico limite risulta chiaramente individuato (rottura generale).
In un terreno molto sciolto, invece, la relazione carichi-cedimenti presenta un tratto curvilineo accentuato fin dai carichi più bassi per effetto di una rottura progressiva del terreno (rottura locale); di conseguenza l'individuazione del carico limite non è così chiara ed evidente come nel caso dei terreni compatti.
Per i terreni molto sciolti, Terzaghi consiglia di prendere in considerazione nel calcolo del carico limite, il valore che si calcola con la formula precedente introducendo però dei valori ridotti delle caratteristiche meccaniche del terreno e precisamente:
![]()
![]()
Esplicitando i coefficienti della formula precedente, la formula di Terzaghi può essere scritta:
![]()
dove:
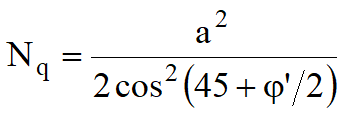
![]()
![]()
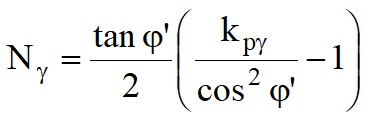
Meyerhof (1963)
Meyerhof propose una formula per il calcolo del carico limite simile a quella di Terzaghi.; le differenze consistono nell'introduzione di ulteriori coefficienti di forma.
Egli introdusse un coefficiente sq' che moltiplica il fattore Nq, fattori di profondità di ed ii pendenza, per il caso in cui il carico trasmesso alla fondazione è inclinato sulla verticale.
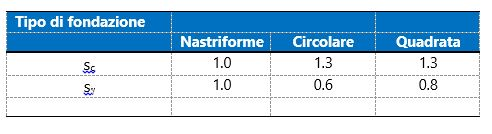
I valori dei coefficienti N furono ottenuti da Meyerhof ipotizzando vari archi di prova BD (v. meccanismo Prandtl), considerando valori approssimati del taglio che si sviluppa nel terreno al di sopra del piano di posa. I fattori di N vengono riportati in Tabella.
|
|
![]()
![]()
![]()
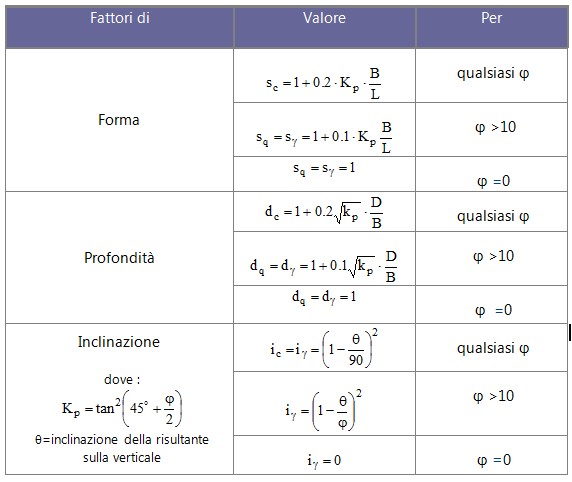
Fattori di forma, profondità ed inclinazione che compaiono nella formula di Meyerhof
Hansen (1970)
E' una ulteriore estensione della formula di Meyerhof; le estensioni consistono nell'introduzione di bi che tiene conto della eventuale inclinazione sull'orizzontale del piano di posa e un fattore gi per terreno in pendenza. La formula di Hansen vale per qualsiasi rapporto D/B, quindi sia per fondazioni superficiali che profonde, ma lo stesso autore introdusse dei coefficienti per meglio interpretare il comportamento reale della fondazione (vedi Tabella), senza di essi, infatti, si avrebbe un aumento troppo forte del carico limite con la profondità.
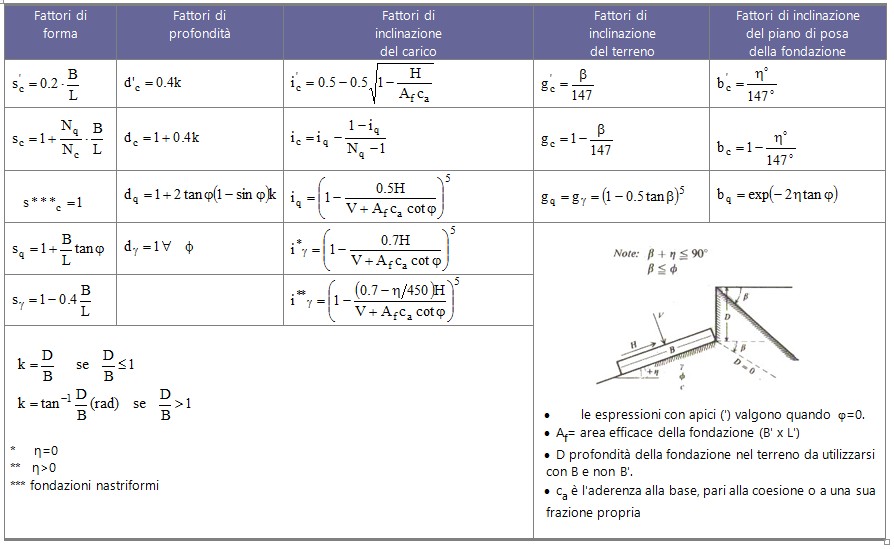
Fattori proposti da Hansen per il calcolo del qlim

Fattori di profondità per ϕ =0
Vesic (1975)
La formula di Vesic è analoga alla formula di Hansen, con Nq ed Nc come per la formula di Meyerhof ed Ng come sotto riportato:
![]()
I fattori di forma e di profondità che compaiono nelle formule del calcolo della capacità portante sono uguali a quelli proposti da Hansen; alcune differenze sono invece riportate nei fattori di inclinazione del carico, del terreno (fondazione su pendio) e del piano di fondazione (base inclinata).
Brinch-Hansen (EC 7 - EC 8)
Affinché una fondazione possa sostenere il carico di progetto con sicurezza nei riguardi della rottura generale, per tutte le combinazioni di carico relative allo SLU (stato limite ultimo), deve essere soddisfatta la seguente disuguaglianza per tutte le combinazioni di carico relative allo SLU (stato limite ultimo):
![]()
dove:
• Vd è il carico di progettto allo SLU, normale alla base della fondazione, comprendente anche il peso della fondazione stessa;
• Rd è il carico limite di progetto della fondazione nei confronti di carichi normali , tenendo conto anche dell’effetto di carichi inclinati o eccentrici.
Nella valutazione analitica del carico limite di progetto Rd, nei terreni a grana fine, si devono considerare le situazioni a breve e a lungo termine.
Il carico limite di progetto in condizioni non drenate si calcola come:

dove:

Per le condizioni drenate il carico limite di progetto è calcolato come segue.
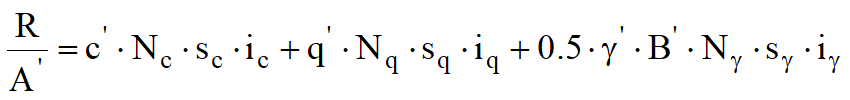
dove:
|
|
|

Fattori correttivi proposti da Brinch-Hansen nel calcolo di qlim
Oltre ai fattori correttivi riportati nella Tabella precedente verranno considerati quelli complementari della profondità del piano di posa e dell’inclinazione del piano di posa e del piano campagna (Hansen).
Meyerhof e Hanna (1973)
Tutta la trattazione teorica della rottura per carico limite del terreno è stata basata sull'ipotesi che il terreno di fondazione sia omogeneo ed isotropo fino a notevole profondità.
Tale ipotesi però non rispecchia la realtà perchè, in natura, il terreno presenta disomogeneità litologica per cui può essere costituito da diverse percentuali delle componenti granulometriche come ghiaia, sabbia, limo e argilla.
Le relazioni per la stima del carico limite, ricavate dall'ipotesi di terreno omogeneo risultano essere molto approssimative se il terreno è stratificato, soprattutto se le superfici di rottura interferiscono con i limiti degli strati del terreno.
Si consideri un sistema costituito da due strati di terreno distinti ed una fondazione posizionata sullo strato superiore a profondità D dal piano campagna, le superfici di rottura a carico limite possono svilupparsi completamente sullo strato superiore oppure coinvolgere anche il secondo strato. Può accadere che lo strato superiore sia più resistente rispetto allo strato inferiore o viceversa.
In entrambi i casi verrà presentata un'analisi generale per (c =0) e si dimostrerà che la stessa analisi sarà valida anche nel caso di terreni sabbiosi o argillosi.
Lo studio della capacità portante di un sistema a strati è stato affrontato da diversi autori: Button (1953), Vesic (1975), Meyerhof (1974), Meyerhof e Hanna (1978)
Meyerhof (1974) ha analizzato un sistema a due strati composto da sabbia densa su argilla morbida e sabbia sciolta su argilla rigida e ha supportato il suo studio con alcuni test su modello. Successivamente Meyerhof e Hanna (1978) hanno integrato lo studio di Meyerhof (1974) includendo nelle analisi il terreno privo di coesione.
Si riporta la trattazione di Meyerhof (1974) e Meyerhof e Hanna (1978).
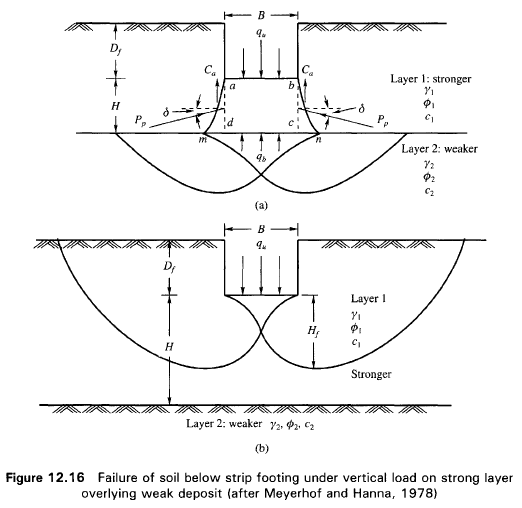
Caso 1: strato più resistente che sovrasta un deposito più debole
Nella figura 12.16 (a) è rappresentata una fondazione di larghezza B e profondità D in uno strato di terreno resistente (strato 1). Lo strato debole si trova a distanza H dal piano di posa della fondazione.
Se si verificano le condizioni per cui la distanza H non è sufficientemente ampia, oppure, si ha un carico eccezionale, una parte dello stesso carico verrà trasferito oltre il livello mn. Questa condizione indurrà il formarsi di superfici di rottura anche nello strato più debole (strato 2). Se la distanza H è relativamente grande, le superfici di rottura si svilupperanno completamente nello strato 1 come evidenziato in Figura 12.16b.
Il carico limite negli strati 1 e 2 può essere espresso dalle seguenti relazioni:
Strato 1
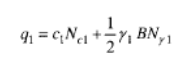
Strato 2
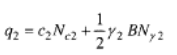
Dove:
Nc1, Nγ1 = fattori di capacità portante dello strato 1 con angolo di resistenza a taglio φ1
Nc2, Nγ2 = fattori di capacità portante dello strato 2 con angolo di resistenza a taglio φ2
Se il piano di posa della fondazione si trova ad una distanza Df rispetto al piano campagna e la distanza H è relativamente grande l'espressione del carico limite è la seguente:
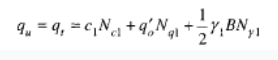
Se q1 è maggiore di q2 e se la distanza H non è sufficiente a formare una condizione di plasticizzazione completa nello strato 1, allora la rottura è legata alla spinta del terreno che si sviluppa dallo strato più debole allo strato più resistente. La formulazione per la stima del carico limite diventa:
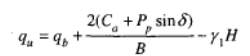
Dove:
qb= carico limite nello strato 2
Pp= spinta passiva
δ= angolo di inclinazione della spinta passiva rispetto all'orizzontale
Ca= adesione
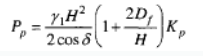
Caso 2: strato superiore denso, strato inferiore argilla satura (φ2=0)
IL valore del carico limite per lo strato più denso può essere espresso dalla relazione seguente:
![]()
Operando opportune sostituzioni si ottiene:
![]()
Per c1=0 qt si ricava da:
![]()
L'espressione del carico limite qu valida per fondazioni rettangolari è:
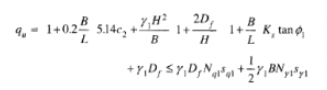
Caso 3: strato superiore sabbia densa , strato inferiore sabbia sciolta (C1=C2=0)
In questo caso il valore del carico limite può essere espresso da:
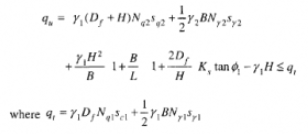
Caso 4: strato superiore argilla rigida satura (φ1=0), strato inferiore argilla molle satura (φ2=0)
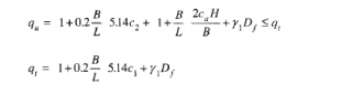
Richards, Elms e Budhu (1993) hanno sviluppato una procedura che consente, in condizioni sismiche, di valutare sia il carico limite sia i cedimenti indotti, e quindi di procedere alle verifiche di entrambi gli stati limite (ultimo e di danno). La valutazione del carico limite viene perseguita mediante una semplice estensione del problema del carico limite al caso della presenza di forze di inerzia nel terreno di fondazione dovute al sisma, mentre la stima dei cedimenti viene ottenuta mediante un approccio che segue il metodo di Newmark (cfr. Appendice H di “Aspetti geotecnici della progettazione in zona sismica” – Associazione Geotecnica Italiana ). Glia autori hanno esteso la classica formula trinomia del carico limite nel seguente modo:
![]()
Dove i fattori di capacità portante vengono calcolati con le seguenti formule:
![]()
![]()
![]()
Gli autori hanno, inoltre, esaminato un meccanismo di tipo Coulomb, con un approccio che segue quello dell'equilibrio limite, considerando anche le forze d'inerzia agenti sul volume di terreno a rottura. In campo statico, il classico meccanismo di Prandtl può essere infatti approssimato come mostrato nella Figura che segue, eliminando la zona di transizione (ventaglio di Prandtl) ridotta alla sola linea AC, che viene considerata come una parete ideale in equilibrio sotto l’azione della spinta attiva e della spinta passiva che riceve dai cunei I e III:
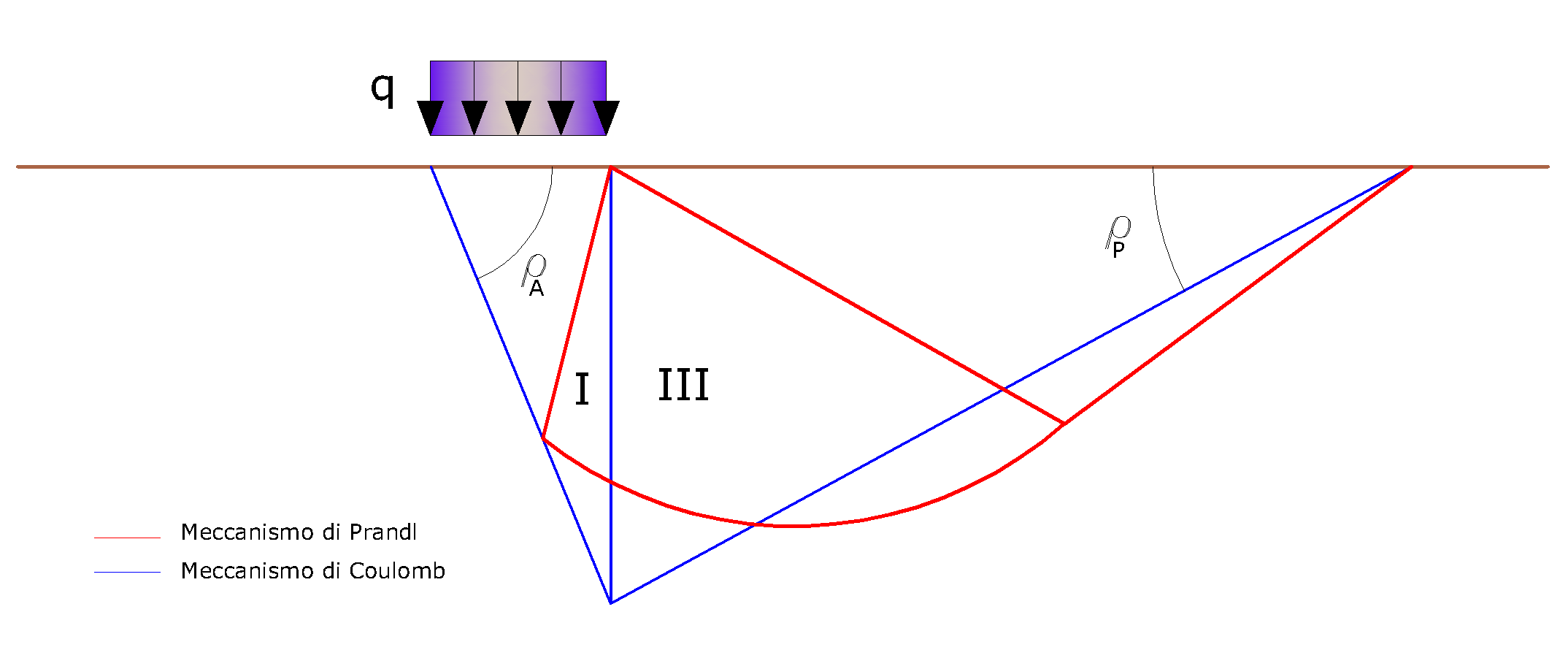
Schema di calcolo del carico limite (qlim)
Gli autori hanno ricavato le espressioni degli angoli ρA e ρP che definiscono le zone di spinta attiva e passiva, e dei coefficienti di spinta attiva e passiva KA e KP in funzione dell’angolo di attrito interno φ del terreno e dell’angolo di attrito δ terreno – parete ideale:
![]()
![]()
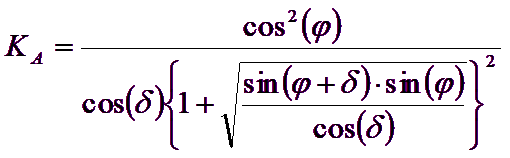
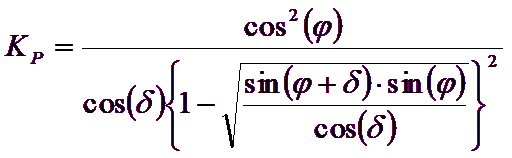
E’ comunque da osservare che l’impiego delle precedenti formule assumendo φ=0.5δ, conduce a valore dei coefficienti di carico limite molto prossimi a quelli basati su un analisi di tipo Prandtl. Richards et al. (1993) hanno quindi esteso l’applicazione del meccanismo di Coulomb ( al caso sismico, portando in conto le forze d’inerzia agenti sul volume di terreno a rottura. Tali forze di massa, dovute ad accelerazioni kh g e kv g, agenti rispettivamente in direzione orizzontale e verticale, sono a loro volta pari a kh g e kv g. Sono state così ottenute le estensioni delle espressioni di ρa e ρp, nonché di KA e KP, rispettivamente indicate come ρAE e ρPE e come KAE e KPE per denotare le condizioni sismiche:
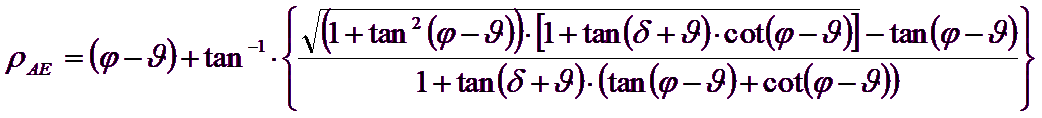
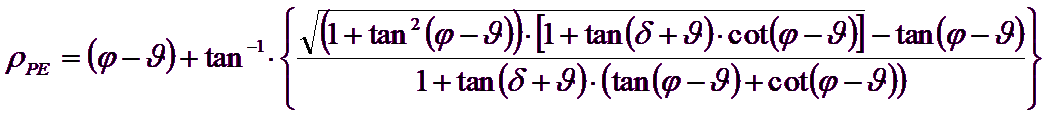
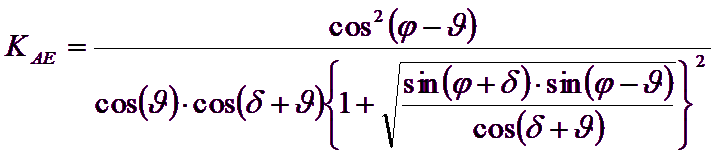
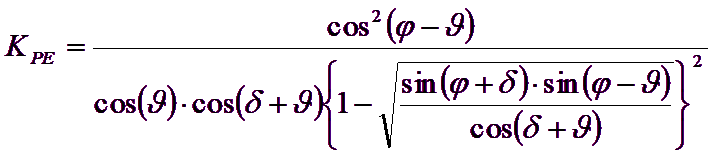
I valori di Nq e Ng sono determinabili ancora avvalendosi delle formule precedenti, impiegando naturalmente le espressioni degli angoli ρAE e ρPE e dei coefficienti KAE e KPE relative al caso sismico. In tali espressioni compare l’angolo θ definito come:

Nella Tabella sono mostrati i fattori di capacità portante calcolati per i seguenti valori dei parametri:
φ = 30°
δ = 15°
E per diversi valori dei coefficienti di spinta sismica:
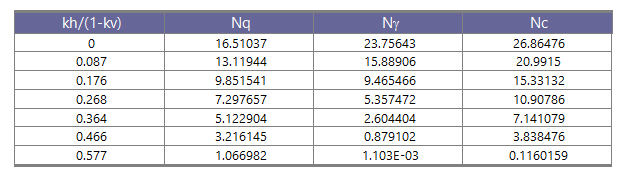
Tabella dei fattori di capacità portante per φ=30°
Carico limite di fondazioni su roccia
Per la valutazione della capacità portante ammissibile delle rocce si deve tener conto di alcuni parametri significativi quali le caratteristiche geologiche, il tipo di roccia e la sua qualità, misurata con l' RQD. Nella capacità portante delle rocce si utilizzano normalmente fattori di sicurezza molto alti e legati in qualche modo al valore del coefficiente RQD: ad esempio, per una roccia con RQD pari al massimo pari a 0.75 il fattore di sicurezza varia tra 6 e 10. Per la determinazione della capacità portante di una roccia si possono usare le formule di Terzaghi, usando angolo d'attrito e coesione della roccia, o quelle proposte in un capitolo di Deere nel libro di Stagg e Zienkiewicz (1968) in cui i coefficienti della formula della capacità portante valgono:
|
|
|
Con tali coefficienti vanno usati i fattori di forma impiegati nella formula di Terzaghi.
La capacità portante ultima calcolata è comunque funzione del coefficiente RQD secondo la seguente espressione:
![]()
Se il carotaggio in roccia non fornisce pezzi intatti (RQD tende a 0), la roccia viene trattata come un terreno stimando al meglio i parametri c e φ.
Verifica a slittamento
In conformità con i criteri di progetto allo SLU, la stabilità di un plinto di fondazione deve essere verificata rispetto al collasso per slittamento oltre a quello per rottura generale. Rispetto al collasso per slittamento la resistenza viene valutata come somma di componenti: una delle componenti è dovuta all’adesione, l'altra è dovuta all’attrito fondazione-terreno. La resistenza laterale derivante dalla spinta passiva del terreno può essere messa in conto secondo una percentuale indicata dall’utente. La resistenza di calcolo per attrito ed adesione è valutata secondo l’espressione:
![]()
dove:
Nsd è il valore di calcolo della forza verticale;
δ è l’angolo di resistenza a taglio alla base della fondazione;
ca è l’adesione plinto-terreno;
A' è l’area della fondazione efficace, intesa, in caso di carichi eccentrici, come area ridotta al centro del applicata la risultante.
Calcolo dei cedimenti
L'applicazione di un carico di dimensioni finite su un terreno coesivo genera una serie di fenomeni che possono essere schematizzati come illustrato in Figura.
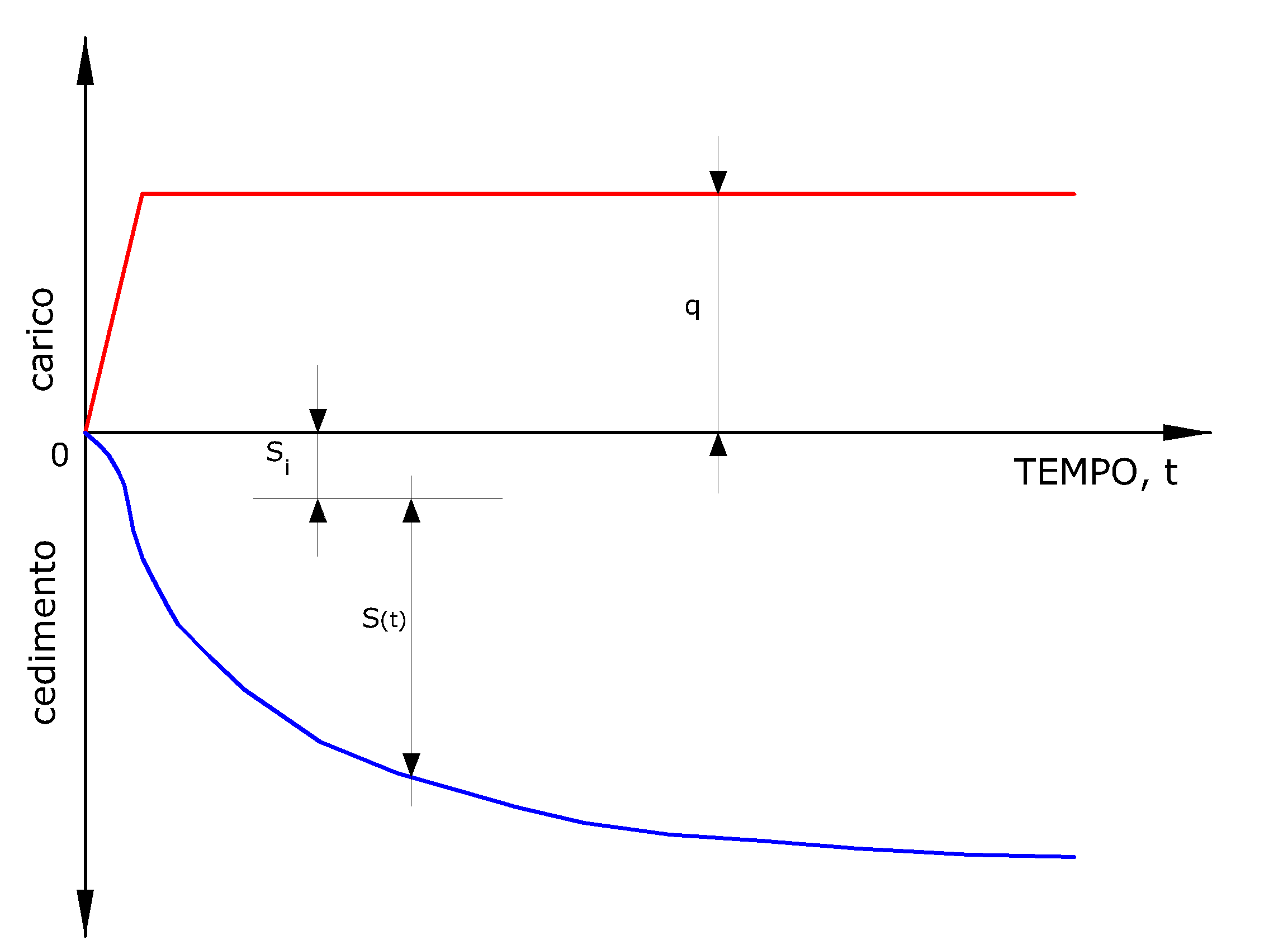
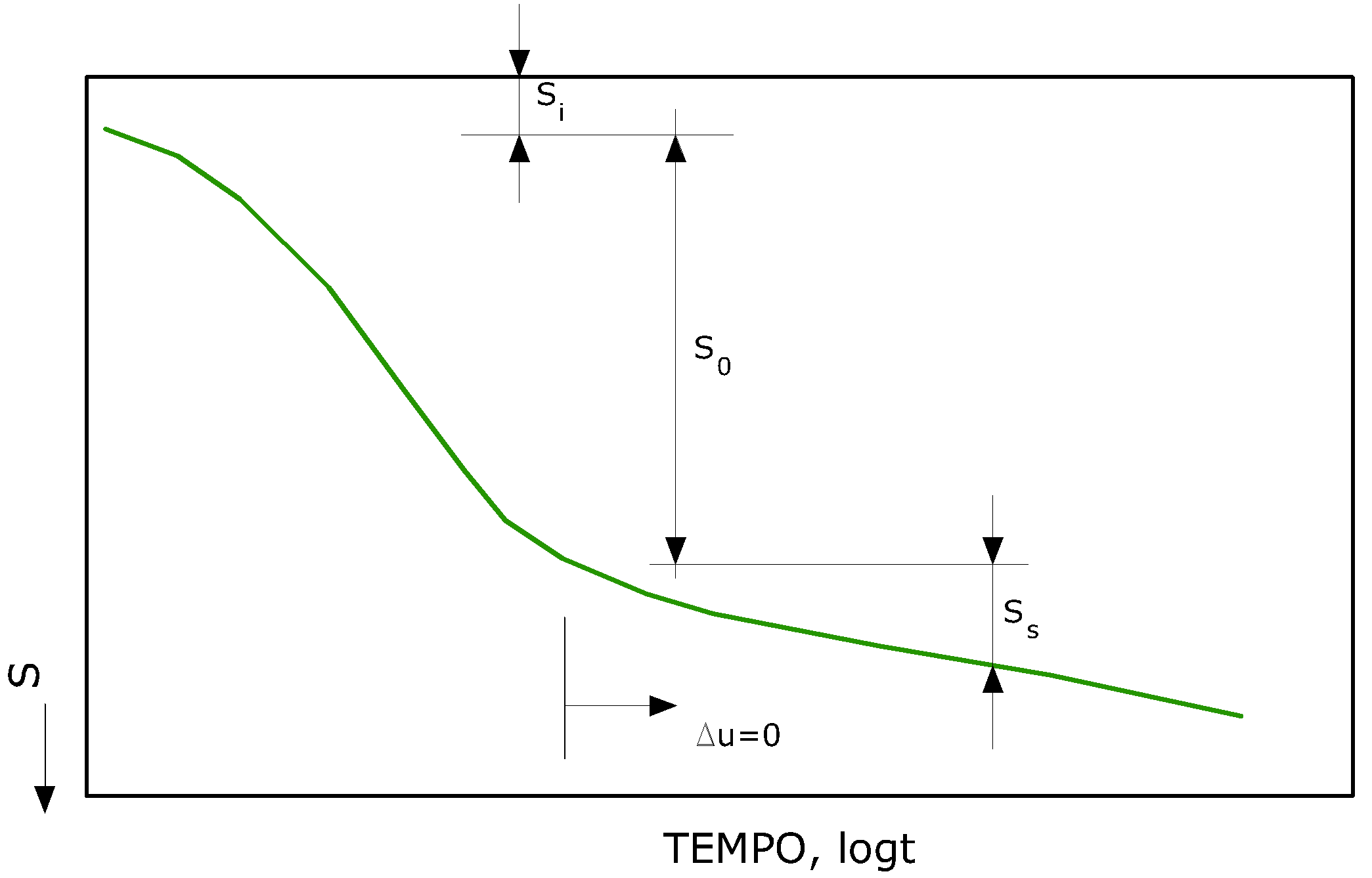
Tipi di cedimento
1.Durante la fase di carico si sviluppano nel terreno delle sovrapressioni dell'acqua interstiziale Δu, e data la bassa permeabilità del terreno è lecito assumere che, nell'ambito delle usuali velocità di applicazione del carico, ci si trovi in condizioni non drenate.Lo strato di argilla si deforma a volume pressochè costante e il cedimento che ne consegue è indicato come cedimento immediato.
2.L'instaurarsi del drenaggio, con il progressivo trasferimento del carico dalla fase fluida allo scheletro solido, comporta ulteriori cedimenti, la cui velocità nel tempo è legata principalmente alle condizioni di drenaggio. Il processo è noto come consolidazione primaria l'analisi viene condotta con i vari modelli della teoria della consolidazione. Il cedimento che consegue a tale processo di espulsione dell'acqua dai vuoti interstiziali è indicato come cedimento di consolidazione.
3.Infine,anche quando le sovrapressioni interstiziali ai sono dissipate (Δu=0), continuano ad esserci nel tempo assestamenti dovuti a deformazioni viscose in condizioni drenate, e il cedimento è noto come cedimento secondario .
Il comportamento dei terreni a grana grossa (sabbie e ghiaie) risulta macroscopicamente diverso da quelli a grana fine (limi ed argille) a causa della diversa permeabilità.
In questo caso si parlerà di cedimento iniziale e secondario per indicare gli assestamenti di natura elasto-plastica e quelli dovuti a fenomeni di natura viscosa.
I cedimenti di una fondazione rettangolare di dimensioni B'x L' posta sulla superficie di un semispazio elastico si possono calcolare in base ad una equazione basata sulla teoria dell'elasticità (Timoshenko e Goodier, 1951):
![]() (1)
(1)
dove:
q0 è intensità della pressione di contatto;
B' è la minima dimensione dell'"area reagente";
Es e m sono i parametri elastici del terreno;
Ii =f(L'/B', H, m, D) sono i coefficienti di influenza dipendenti dal rapporto L'/B', spessore dello strato H, coefficiente di Poisson ν, profondità del piano di posa D.
IF coefficiente di influenza.
I coefficienti I1 e I2 si possono calcolare utilizzando le equazioni fornite da Steinbrenner (1934) (V. Bowles), in funzione del rapporto M=L'/B' ed N=H/B, utilizzando B'=B/2 e L'=L/2 per i coefficienti Ii relativi al centro e B'=B e L'=L per i coefficienti Ii relativi al bordo. Il coefficiente di influenza IF deriva dalle equazioni di Fox (1948), che indicano il cedimento si riduce con la profondità in funzione del coefficiente di Poisson e del rapporto L/B. In modo da semplificare l'equazione (1) si introduce il coefficiente IS:
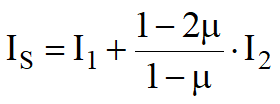
Si può scrivere la relazione (1) nella forma più compatta:
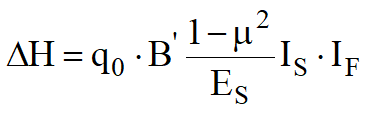
L'equazione può applicarsi a fondazioni flessibili o rigide con opportune modifiche del valore di Is.
L'autore analizzando un certo numero di casi ha concluso che l'equazione formulata precedentemente, per fornire dei buoni risultati deve essere applicata come segue:
1.Effettuare la migliore stima di q0;
2.Covertire la fondazione, se circolare,in una fondazione quadrata equivalente.
3.Determinare il punto dove calcolare il cedimento e suddividere la base di appoggio in modo che il punto si trovi in corrispondenza di uno spigolo esterno ovvero di uno spigolo interno comune a più rettangoli .
4.Lo spessore dello strato H responsabile del cedimento va preso come il minimo dei due seguenti valori : profondità z=5B dove B è la minima dimensione complessiva della base della fondazione; profondità alla quale si trova uno strato duro (ES dello strato deve essere 10 volte circa il valore dello spessore adiacente).
5.Calcolare correttamente il rapporto H/B'. Per uno spessore dello strato H=z=5B si trova, per il centro di fondazione H/B'=5B/0,5B=10B, per uno spigolo 5B/B=5.
6.Ricavare Is operando una stima accurata di m e ricavando i coefficienti di influenza I1 ed I2 dalla tabella proposta dallo stesso autore.
7.Ricavare IF con l'ausilio della Figura seguente.
8.Ottenere Es nello spessore dello strato z=H come media pesata dei valori di Esi dei singoli strati nello spessore Hi.
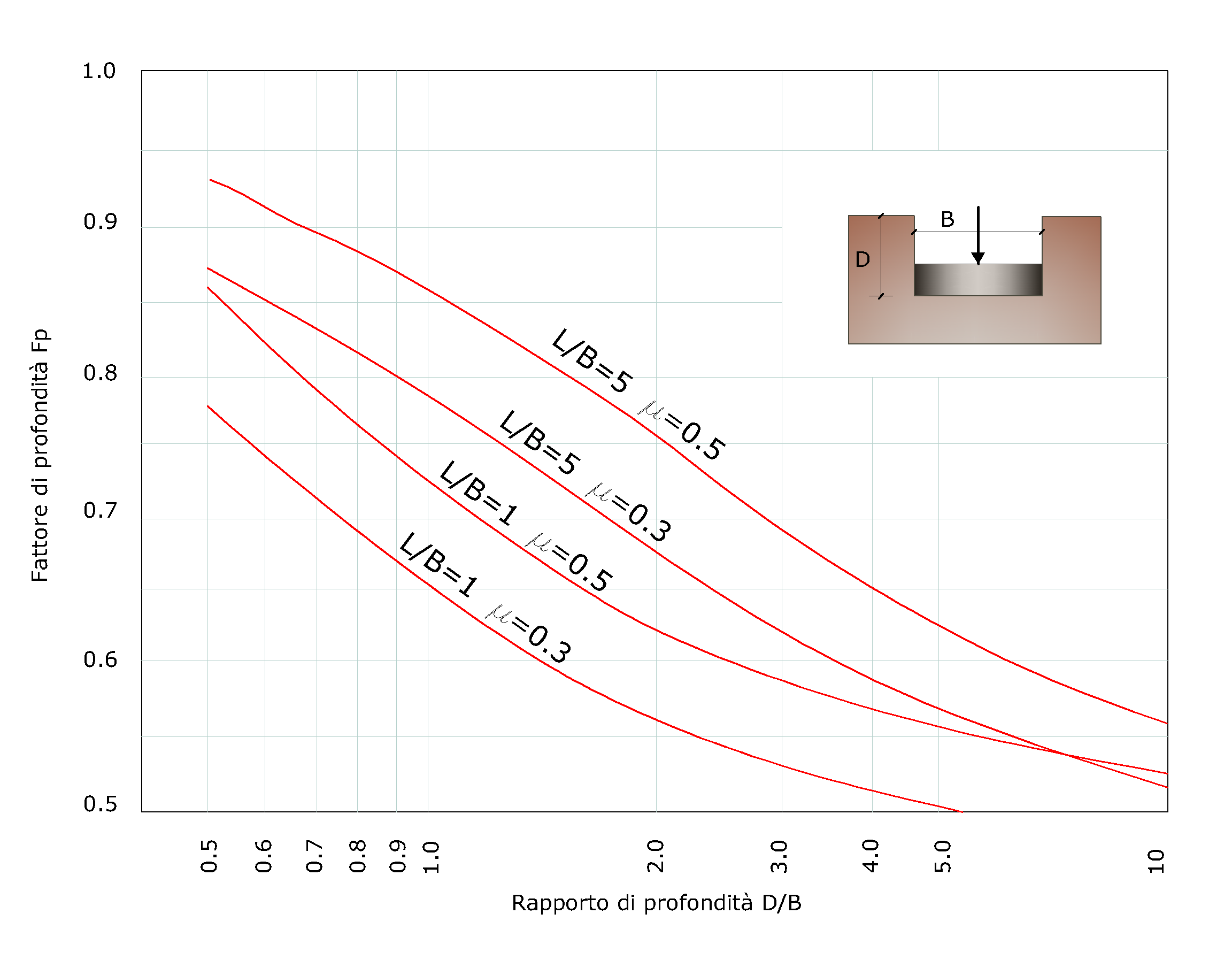
Coefficiente di influenza IF per una fondazione collocata a profondità D.
Il calcolo dei cedimenti con l’approccio edometrico consente di valutare un cedimento di consolidazione di tipo monodimensionale (Terzaghi-1943), prodotto dalle tensioni indotte da un carico applicato in condizioni di espansione laterale impedita. Pertanto la stima effettuata con questo metodo va considerata come empirica, piuttosto che teorica.Tuttavia, la semplicità d’uso e la facilità di controllare l’influenza dei vari parametri che intervengono nel calcolo, ne fanno un metodo molto diffuso.Con riferimento allo schema riportato in Figura, il cedimento ΔH di uno strato di spessore iniziale H0 risulta dato da:
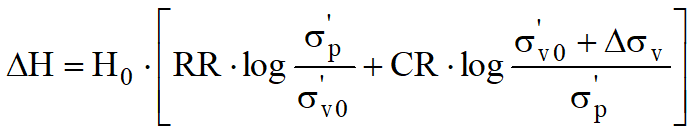
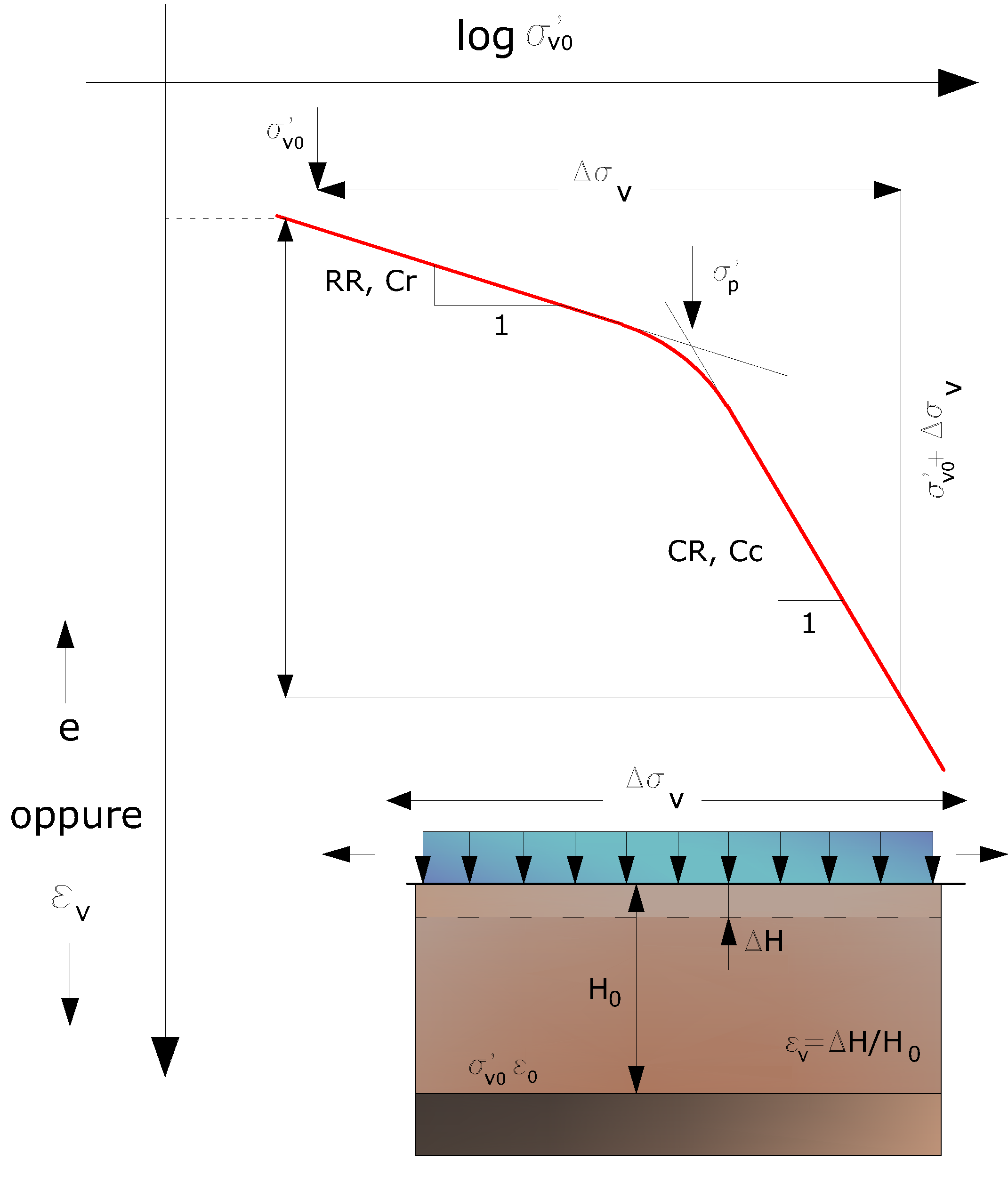
Cedimento edometrico
L’ approccio edometrico nel calcolo dei cedimenti passa essenzialmente attraverso due fasi:
1. il calcolo delle tensioni verticali indotte alle varie profondità con l’applicazione della teoria dell’elasticità (approccio di Boussinesq, Westergaard ...);
2. la valutazione dei parametri di compressibilità attraverso la prova edometrica.
In riferimento ai risultati della prova edometrica, il cedimento è valutato come:
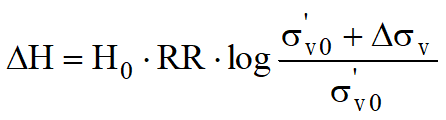
se si tratta di un terreno sovraconsolidato (OCR>1), ossia se l’incremento di tensione dovuto all’applicazione del carico non fa superare la pressione di preconsolidazione σ'p (σ'v0 + Δσv < σ'p).
Se invece il terreno è normalconsolidato (σ'v0=σ'p), le deformazioni avvengono nel tratto di compressione e il cedimento è valutato come:

dove:
RR è il rapporto di ricompressione;
CR è il rapporto di compressione;
H0 è lo spessore iniziale dello strato;
σ'v0 è la tensione verticale efficace prima dell’applicazione del carico;
Δσv è l' incremento di tensione verticale dovuto all’applicazione del carico.
In alternativa ai parametri RR e CR si fa riferimento al modulo edometrico M; in tal caso però occorre scegliere opportunamente il valore del modulo da utilizzare, tenendo conto dell’intervallo tensionale ( σ'v0 + Δσv ) significativo per il problema in esame. L’applicazione corretta di questo tipo di approccio richiede:
•la suddivisione degli strati compressibili in una serie di piccoli strati di modesto spessore (< 2.00 m);
•la stima del modulo edometrico nell’ambito di ciascuno strato;
•il calcolo del cedimento come somma dei contributi valutati per ogni piccolo strato in cui è stato suddiviso il banco compressibile.
Le espressioni sopra riportate per il calcolo del cedimento di consolidazione vengono utilizzate sia per le argille che per le sabbie di granulometria da fina a media, perché il modulo di elasticità impiegato è ricavato direttamente da prove di consolidazione. Tuttavia, per terreni a grana più grossa le dimensioni dei provini edometrici sono poco significative del comportamento globale dello strato e, per le sabbie, risulta preferibile impiegare prove penetrometriche statiche e dinamiche.
Cedimento secondario
Il cedimento secondario è calcolato facendo riferimento alla relazione:

in cui:
Hc è l’altezza dello strato in fase di consolidazione;
Ca è il coefficiente di consolidazione secondaria come pendenza nel tratto secondario della curva cedimento-logaritmo tempo;
T tempo in cui si vuole calcolare il valore del cedimento secondario;
T100 tempo necessario all’esaurimento del processo di consolidazione primaria.
L'ipotesi alla base di tale metodo sono:
•la consolidazione secondaria inizia dopo l'esaurimento del processo di consolidazione primaria;
•il valore di Ca può ritenersi costante durante l'evolversi del cedimento secondario.
Metodo di Schmertmann (1970)
Un metodo alternativo per il calcolo dei cedimenti è quello proposto da Schmertmann (1970) il quale ha correlato la variazione del bulbo delle tensioni alla deformazione. L'autore ha quindi considerato nel suo modello un diagramma delle deformazioni di forma triangolare, vedi Figura in cui la profondità alla quale si hanno deformazioni significative è assunta pari a 4B, nel caso di fondazioni nastriformi, e pari a 2B per fondazioni quadrate o circolari.
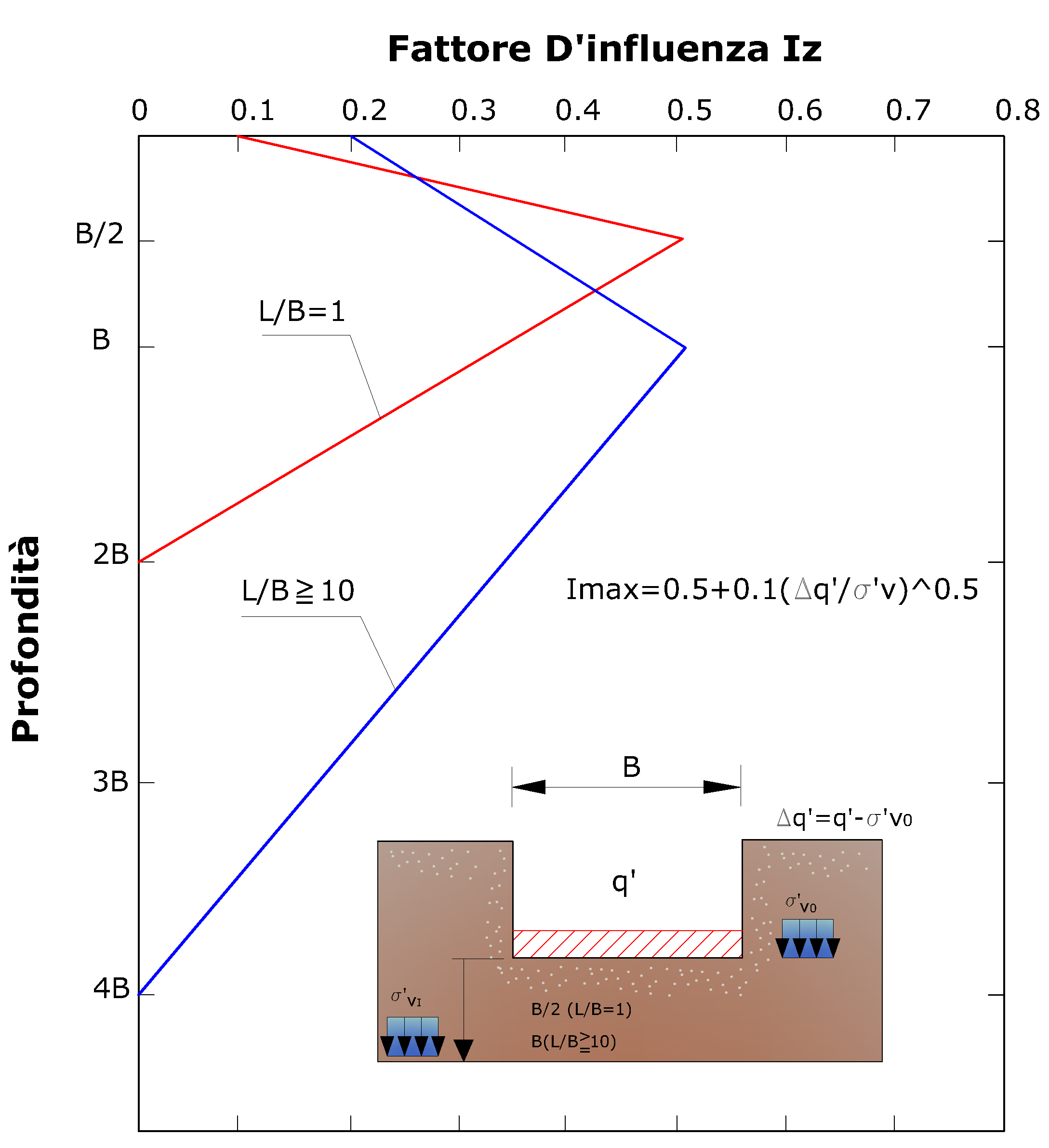
Variazione del fattore di influenza con la profondità
Secondo tale approccio il cedimento si esprime attraverso la seguente espressione:
![]()
nella quale:
Δq rappresenta il carico netto applicato alla fondazione;
Iz è un fattore di deformazione di valore massimo ad una profondità pari a B/2 per fondazione circolare o quadrata e B per fondazione nastriforme.
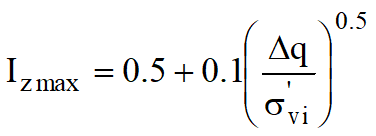
dove:
σ'vi rappresenta la tensione verticale efficace a profondità B/2 per fondazioni quadrate o circolari, e a profondità B per fondazioni nastriformi.
Ei rappresenta il modulo di deformabilità del terreno in corrispondenza dello strato i-esimo considerato nel calcolo;
Δzi rappresenta lo spessore dello strato i-esimo;
C1 e C2 sono due coefficienti correttivi.
Il modulo Ei viene assunto pari a 2.5qc per fondazioni circolari o quadrate e a 3.5qc per fondazioni nastriformi.
Nei casi intermedi, si interpola in funzione del valore di L/B. Il termine qc che interviene nella determinazione di Ei rappresenta la resistenza alla punta fornita dalla prova CPT. Le espressioni utilizzate per i due coefficienti C1 e C2 sono:
|
che tiene conto della profondità del piano di posa. |
|
che tiene conto delle deformazioni differite nel tempo per effetto secondario. |
Nell'espressione t rappresenta il tempo, espresso in anni a costruzione completata, in corrispondenza del quale si calcola il cedimento.
Qualora si disponga di dati ottenuti da prove penetometriche dinamiche per il calcolo dei cedimenti è possibile fare affidamento al metodo di Burland e Burbidge (1985), nel quale viene correlato un indice di compressibilità Ic al risultato NSPT della prova penetrometrica dinamica. L'espressione del cedimento proposta dai due autori è la seguente:
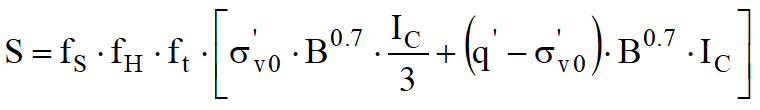
nella quale:
q' è la pressione efficace lorda;
σ'v0 è la tensione verticale efficace alla quota d'imposta della fondazione;
B è la larghezza della fondazione;
Ic è l'indice di compressibilità;
fS, fH, ft sono fattori correttivi che tengono conto rispettivamente della forma, dello spessore dello strato compressibile e della componente viscosa dei cedimenti.
L' indice di compressibilità Ic è legato al valore medio NAV delle Nspt all'interno di una profondità significativa zi:
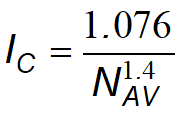
•Per calcolare il valore di zi viene utilizzata la seguente relazione:
![]()
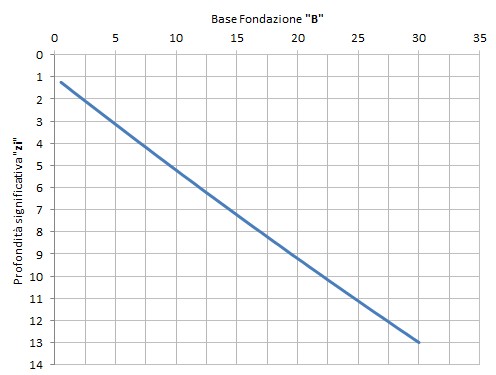
Andamento della Profondità significativa
in funzione della base della fondazione
Per quanto riguarda i valori di Nspt da utilizzare nel calcolo del valore medio NAV va precisato che i valori vanno corretti, per sabbie con componente limosa sotto falda e Nspt>15, secondo l'indicazione di Terzaghi e Peck (1948)
![]()
dove Nc è il valore corretto da usare nei calcoli.
Per depositi ghiaiosi o sabbioso-ghiaiosi il valore corretto è pari a:
![]()
Le espressioni dei fattori correttivi fS, fH ed ft sono rispettivamente:
|
|
|
con:
t = tempo in anni > 3;
R3 = costante pari a 0.3 per carichi statici e 0.7 per carichi dinamici;
R = 0.2 nel caso di carichi statici e 0.8 per carichi dinamici.
|
© GeoStru