È consuetudine nella pratica progettuale valutare le pressioni agenti sul terreno adottando un approccio preso in prestito dalla meccanica strutturale; si considera la sezione di imposta della fondazione come presso-inflessa.
Il calcolo della pressione di progetto viene eseguito considerando la sezione parzialmente reagente e con distribuzione triangolare delle pressioni sul terreno.
Il caso generale è quello di un solido di De Saint Venant sollecitato a sforzo normale eccentrico, quando la risultante delle forze esterne, agenti sulla base libera, si riduce ad uno sforzo normale N e un momento sollecitante M. Un sistema così sollecitato è staticamente equivalente ad una forza N diretta lungo l'asse del solido, applicata in un punto C, detto centro di sollecitazione, diverso dal baricentro G della sezione parzialmente reagente. La congiungente CG fornisce la direzione dell'asse di sollecitazione, coniugata a quella dell'asse neutro definito come l'antipolare del centro C di sollecitazione rispetto all'ellisse centrale d'inerzia della sezione reagente.
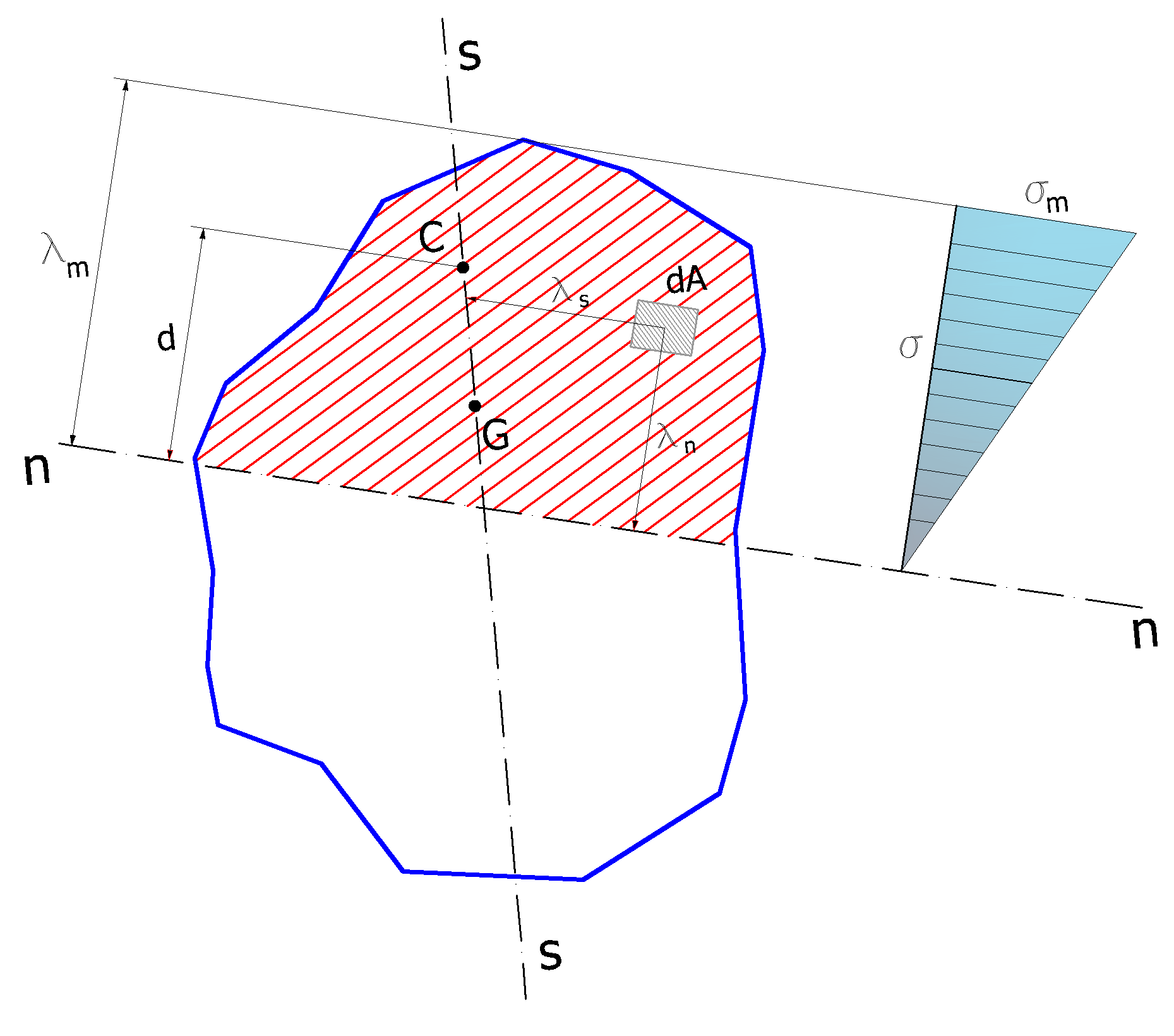
Le incognite del problema, nell' ipotesi di validità del principio di conservazione delle sezioni piane e di validità della legge di Hooke, sono tre:
•due fissano la posizione dell'asse neutro;
•un'altra incognita è rappresentata dal valore della tensione in un punto generico della sezione.
La soluzione del problema viene affrontata da un sistema di tre equazioni:
1.Equazione di equilibrio alla traslazione nella direzione normale alla sezione:
![]()
2.Equazione di equilibrio alla rotazione rispetto all'asse neutro:
![]()
3.Equazione di equilibrio alla rotazione rispetto all'asse di sollecitazione:
![]()
Dalle ipotesi di partenza si può scrivere la seguente relazione:
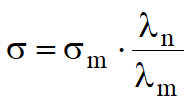
Sostituendo l'equazione precedente nelle tre equazioni di equilibrio, si ottiene:
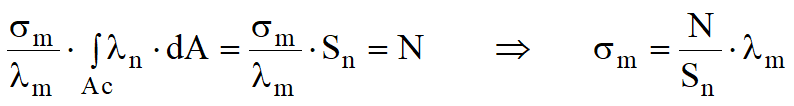

avendo indicato con Sn il momento statico dell'area reagente rispetto all'asse neutro e con In momento d'inerzia della sezione reagente rispetto all'asse neutro, ovvero dalla combinazione dei due risultati si ottiene la posizione dell'asse neutro:
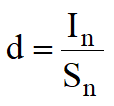
Infine dall'equazione di equilibrio alla rotazione rispetto all'asse di sollecitazione, si ottiene una relazione che esprime la condizione che:
"l'asse neutro e l'asse di sollecitazione sono coniugati rispetto all'ellisse d' inerzia della sezione reagente".
![]()
Nota la posizione dell'asse neutro si può calcolare la tensione in qualsiasi punto della sezione reagente.
© GeoStru