El cálculo del empuje activo con el método de Coulomb se basa en el estudio del equilibrio límite global de un sistema cuyos componentes son el muro y la cuña de terreno homogéneo detrás de la obra implicada en la rotura, asumiendo una pared rugosa.
Para terreno homogéneo y seco el diagrama de las presiones es lineal con distribución:
Pt = Kaγt z
El empuje St es aplicado a 1/3 H con valor:
![]()
Tenemos:
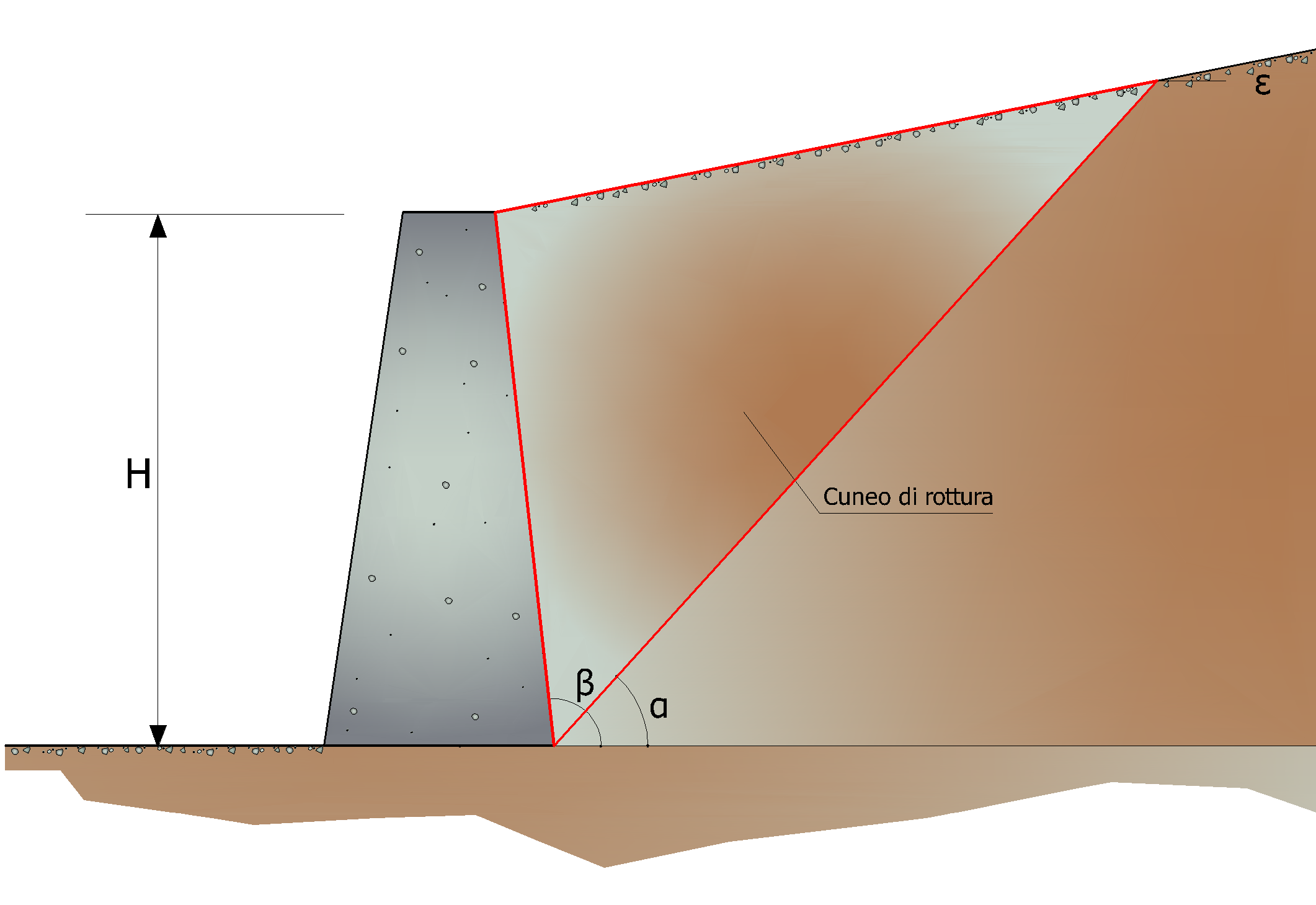
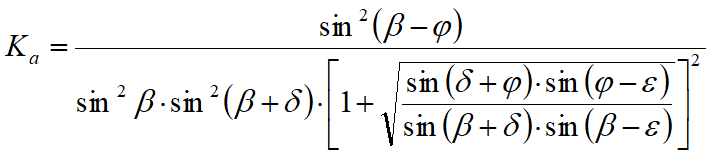
Valores límite de KA:
δ < (β-ϕ-ε) según Muller-Breslau
γt = Peso específico del terreno;
β = Inclinación de la pared interna respecto al plano horizontal pasante por el pie;
ϕ = Ángulo de resistencia al corte del terreno;
δ = Ángulo de rozamiento terreno-muro;
ε = Inclinación del plano del terreno respecto al plano horizontal, positiva si va contra de las manecillas del reloj;
H = Altura de la pared.
Cálculo de empuje activo con Rankine
Si ε = δ= 0 y β = 90° (muro con pared vertical lisa y terraplén horizontal) el empuje St si se simplifica de la siguiente forma:
![]()
coincidiendo con la ecuación de Rankine para el cálculo del empuje activo del terreno con terraplén horizontal.
De hecho, Rankine adoptó esencialmente la mismas hipótesis de Coulomb, con excepción del hecho que omitió el rozamiento terreno-muro y la presencia de cohesión. En su formulación general la expresión de Ka de Rankine se presenta como sigue:
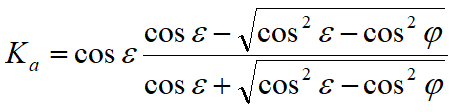
Cálculo del empuje activo con Mononobe & Okabe
El cálculo del empuje activo con el método de Mononobe & Okabe tiene en cuenta el análisis del empuje en condiciones sísmicas con el método pseudo-estático. Se basa en el estudio del equilibrio límite global de un sistema cuyos componentes son el muro y la cuña de terreno homogéneo detrás de la obra implicada en la rotura, con una configuración ficticia de cálculo en la cual el ángulo e, de inclinación del plano del terreno respecto al plano horizontal, y el ángulo β, de inclinación de la pared interna respecto al plano horizontal pasante por el pie, se aumentan en una cantidad θ tal que:
tg θ = kh/(1±kv)
donde kh coeficiente sísmico horizontal y kv vertical.
En ausencia de estudios específicos, los coeficientes kh y kv deben ser calculados de la siguiente manera:
kh = S⋅ag/r kv = 0,5 kh
donde S⋅ag representa el valor de aceleración sísmica máxima del terreno para las diversas categorías de perfil estratigráfico. Al factor r se le puede asignar el valor r = 2 en caso de obras suficientemente flexibles (muros libres de gravedad), mientras que en los otros casos es igual a 1 (muros en h.a. resistentes a flexión, muros en h.a. con pilotes o anclajes, muros de sótano).
Efecto de la cohesión
La cohesión induce presiones negativas constantes iguales a:
![]()
No siendo posible establecer a priori el decremento inducido en el empuje por efecto de la cohesión, ha sido calculada una altura crítica Zc:
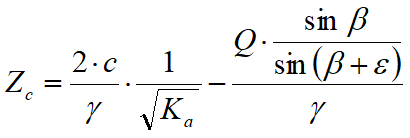
donde:
Q = Carga agente en el terraplén.
Si Zc<0 el efecto se puede aplicar directamente como un decremento cuyo valor es:
Zc = Pc × H
aplicable en H/2.
Carga uniforme en el terraplén
Una carga Q, uniformemente distribuida sobre el plano terreno provoca presiones constantes iguales a:
Pq = Ka·Q·senβ/sen(β+ε
Por integración, un empuje igual a Sq:
![]()
Aplicable en el punto H/2, habiendo indicado con Ka el coeficiente de empuje activo según Muller-Breslau.
Empuje activo en condiciones sísmicas
En presencia de sismo la fuerza de cálculo ejercida por el terraplén sobre el muro está dado por:
![]()
donde:
H = altura muro
kv = coeficiente sísmico vertical
γ = peso específico del terreno
K = coeficiente de empuje activo total (estático + dinámico)
Ews = Empuje hidrostático del agua
Ewd = Empuje hidrodinámico
En terrenos impermeables el empuje hidrodinámico Ewd = 0, pero viene efectuada una corrección en el valor del ángulo θ de la fórmula de Mononobe & Okabe tal que:
![]()
En terrenos con alta permeabilidad en condiciones dinámicas vale siempre la corrección anterior, pero el empuje hidrodinámico asume la siguiente expresión:
![]()
Con H' altura del agua medida a partir de la base del muro.
Empuje hidrostático
El nivel freático con superficie distante Hw de la base del muro provoca presiones hidrostáticas normales en la pared que, en profundidad z, se expresan así:
Pw(z) = γw· z
Con resultante:
Sw = 1/2 ·γw· H²
El empuje del terreno sumergido se obtiene sustituyendo γt con γ't(γ't = γsaturado - γw), peso eficaz del material sumergido en agua.
Resistencia pasiva
Para terreno homogéneo el diagrama de las presiones es lineal del tipo:
Pt = Kp· γt· z
Por integración se obtiene el empuje pasivo:
![]()
Habiendo indicado con:
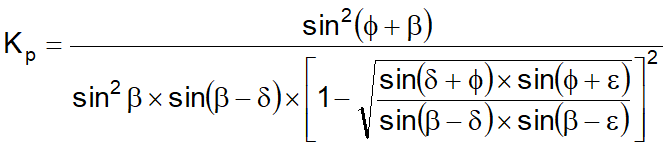
(Muller-Breslau) con valores límites de δ iguales a:
δ< β-ϕ-ε
La expresión de Kp según Rankine asume la siguiente forma:
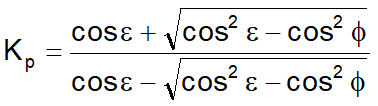
© Geostru