Il calcolo della spinta attiva con il metodo di Coulomb è basato sullo studio dell'equilibrio limite globale del sistema formato dal muro e dal prisma di terreno omogeneo retrostante l'opera e coinvolto nella rottura nell'ipotesi di parete ruvida.
Per terreno omogeneo ed asciutto il diagramma delle pressioni si presenta lineare con distribuzione:
Pt = Kaγt z
La spinta St è applicata ad 1/3 H di valore:
![]()
Avendo indicato con:
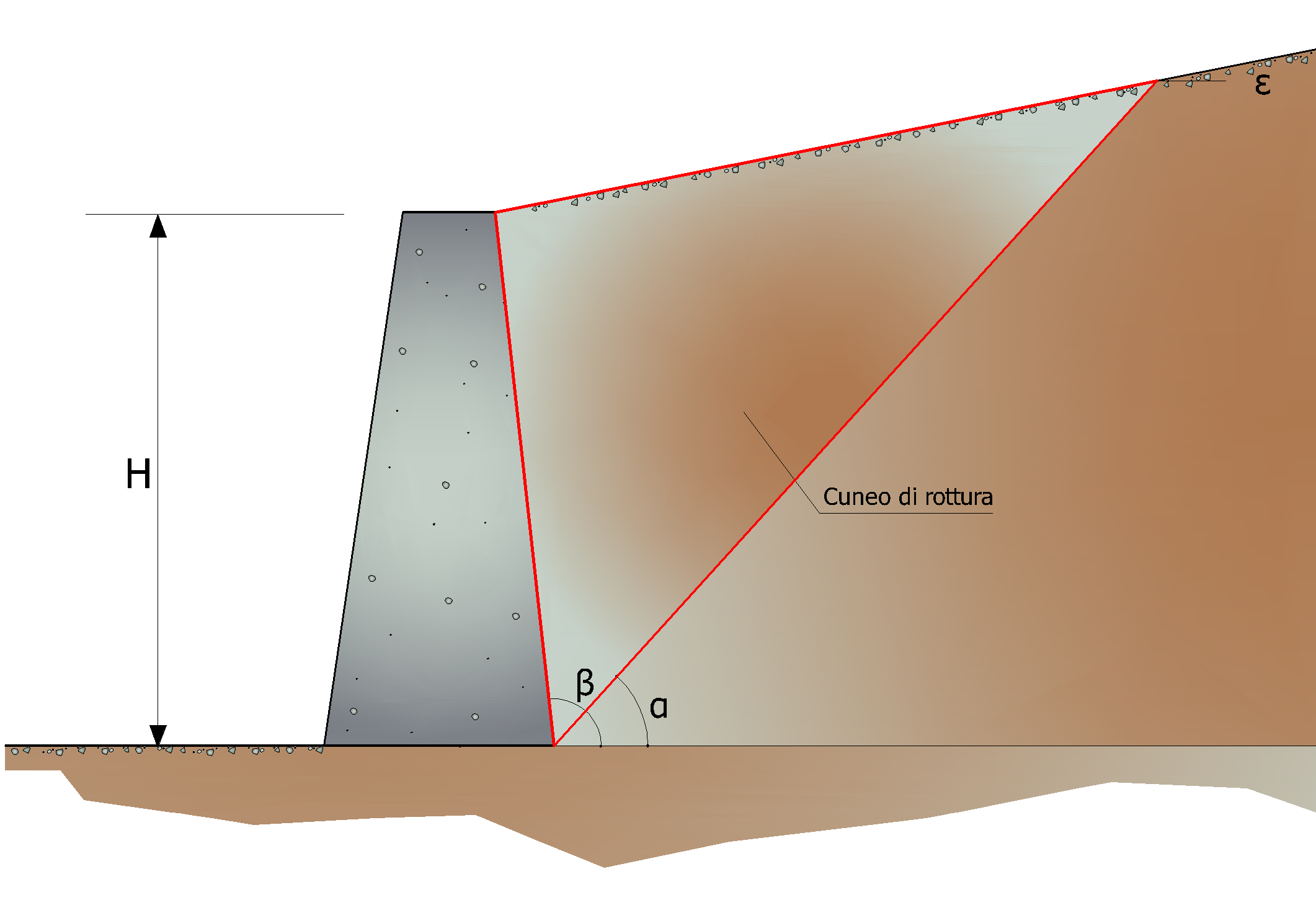
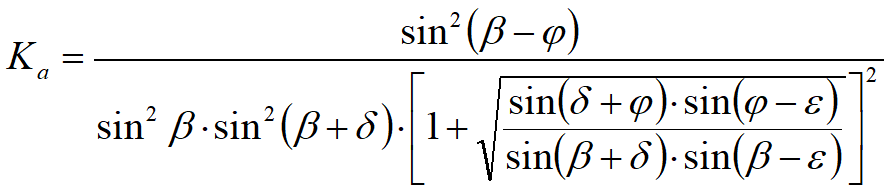
Valori limiti di KA:
δ < (β-φ-ε) secondo Muller-Breslau
γt = Peso unità di volume del terreno;
β = Inclinazione della parete interna rispetto al piano orizzontale passante per il piede;
φ = Angolo di resistenza al taglio del terreno;
δ = Angolo di attrito terra-muro;
ε = Inclinazione del piano campagna rispetto al piano orizzontale, positiva se antioraria;
H = Altezza della parete.
Calcolo della spinta attiva con Rankine
Se ε = δ = 0 e β= 90° (muro con parete verticale liscia e terrapieno con superficie orizzontale) la spinta St si semplifica nella forma:
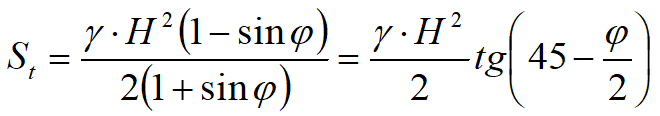
che coincide con l’equazione di Rankine per il calcolo della spinta attiva del terreno con terrapieno orizzontale.
In effetti Rankine adottò essenzialmente le stesse ipotesi fatte da Coulomb, ad eccezione del fatto che trascurò l’attrito terra-muro e la presenza di coesione. Nella sua formulazione generale l’espressione di
Ka di Rankine si presenta come segue:
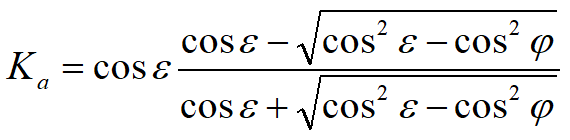
Calcolo della spinta attiva con Mononobe & Okabe
Il calcolo della spinta attiva con il metodo di Mononobe & Okabe riguarda la valutazione della spinta in condizioni sismiche con il metodo pseudo-statico. Esso è basato sullo studio dell'equilibrio limite globale del sistema formato dal muro e dal prisma di terreno omogeneo retrostante l'opera e coinvolto nella rottura in una configurazione fittizia di calcolo nella quale l’angolo ε, di inclinazione del piano campagna rispetto al piano orizzontale, e l’angolo β, di inclinazione della parete interna rispetto al piano orizzontale passante per il piede, vengono aumentati di una quantità θ tale che:
tg θ = kh/(1±kv)
con kh coefficiente sismico orizzontale e kv verticale.
In assenza di studi specifici, i coefficienti kh e kv devono essere calcolati come:
kh = S·ag/r kv = 0,5·kh
in cui S×ag rappresenta il valore dell’accelerazione sismica massima del terreno per le varie categorie di profilo stratigrafico definite dall’Ordinanza P.C.M. n. 3274 del 20.03.2003. Al fattore r viene può essere assegnato il valore r = 2 nel caso di opere sufficientemente flessibili (muri liberi a gravità), mentre in tutti gli altri casi viene posto pari a 1 (muri in c.a. resistenti a flessione, muri in c.a. su pali o tirantati, muri di cantinato).
Effetto dovuto alla coesione
La coesione induce delle pressioni negative costanti pari a:
![]()
Non essendo possibile stabilire a priori quale sia il decremento indotto nella spinta per effetto della coesione, è stata calcolata un’altezza critica Zc come segue:
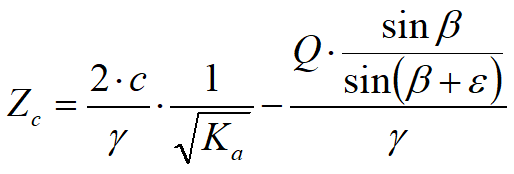
dove:
Q = Carico agente sul terrapieno.
Se Zc<0 è possibile sovrapporre direttamente gli effetti, con decremento pari a:
Sc = Pc× H
con punto di applicazione pari a H/2.
Carico uniforme sul terrapieno
Un carico Q, uniformemente distribuito sul piano campagna induce delle pressioni costanti pari a:
Pq = Ka·Q·senβ/sen(β+ε)
Per integrazione, una spinta pari a Sq:
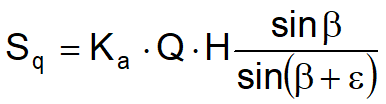
Con punto di applicazione ad H/2, avendo indicato con Ka il coefficiente di spinta attiva secondo Muller-Breslau.
Spinta attiva in condizioni sismiche
In presenza di sisma la forza di calcolo esercitata dal terrapieno sul muro è data da:
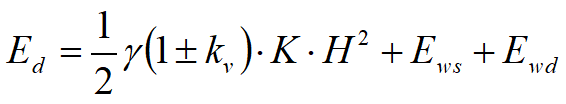
dove:
H= altezza muro
kv= coefficiente sismico verticale
γ = peso per unità di volume del terreno
K = coefficienti di spinta attiva totale (statico + dinamico)
Ews= spinta idrostatica dell’acqua
Ewd = spinta idrodinamica
Per terreni impermeabili la spinta idrodinamica Ewd = 0, ma viene effettuata una correzione sulla valutazione dell’angolo q della formula di Mononobe & Okabe così come di seguito:
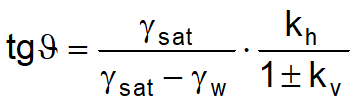
Nei terreni ad elevata permeabilità in condizioni dinamiche continua a valere la correzione di cui sopra, ma la spinta idrodinamica assume la seguente espressione:
![]()
con H' altezza del livello di falda misurato a partire dalla base del muro.
Spinta idrostatica
La falda con superficie distante Hw dalla base del muro induce delle pressioni idrostatiche normali alla parete che, alla profondità z, sono espresse come segue:
Pw(z) = γw· z
Con risultante pari a:
Sw = 1/2 ·γw· H²
La spinta del terreno immerso si ottiene sostituendo γt con γ't(γ't = γsaturo - γw), peso efficace del materiale immerso in acqua.
Resistenza passiva
Per terreno omogeneo il diagramma delle pressioni risulta lineare del tipo:
Pt = Kp· γt· z
per integrazione si ottiene la spinta passiva:
![]()
avendo indicato con:
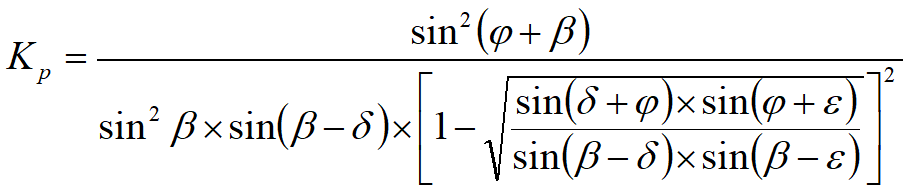
(Muller-Breslau) con valori limiti di δ pari a:
δ< β-φ-ε
L'espressione di Kp secondo la formulazione di Rankine assume la seguente forma:
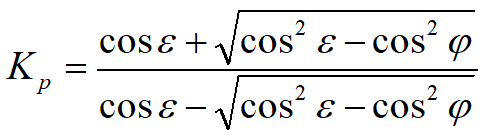
© Geostru