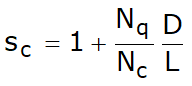The formula for bearing capacity proposed by Terzaghi, reproduced below, assumes that that the soil existing up to the point of embedment, can be substituted by a surcharge equal to the effective vertical tension (ignoring the fact that the interaction between pile and soil may modify this value) and thus reduces the problem to the analysis of bearing capacity of surface foundation.

Terzaghi formula
This may be written:
![]()
where:
|
|
|
|
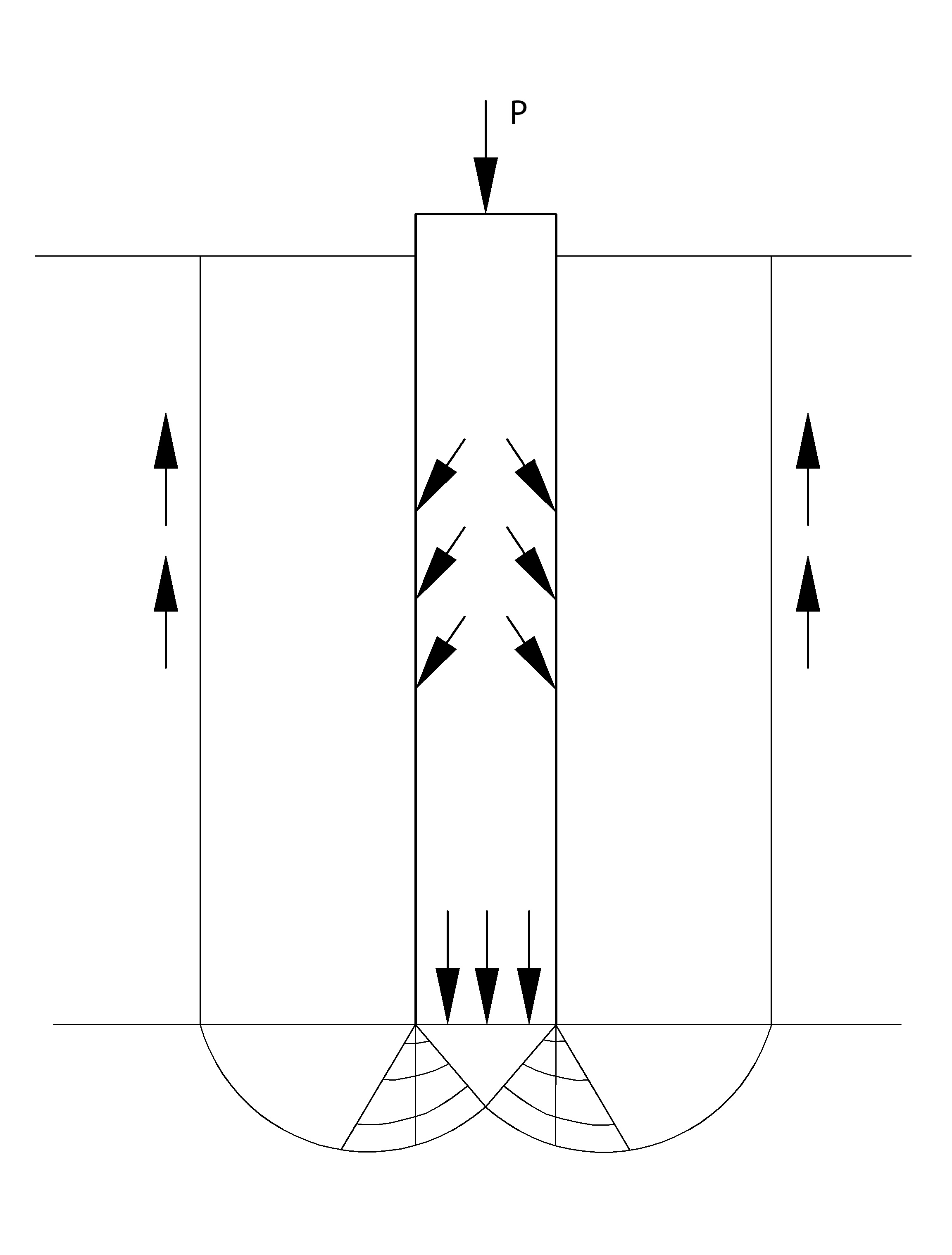
Berezantzev’s method
Fundamentally Berezantzev refers to a slip surface of Terzaghi’s model which terminates at the base level (Pile point/tip) he however considers that the cylinder of soil with the same axis as the pile, whose diameter is the extent of the section of the slip surface, be in some measure sustained by tangential action, by the rest of the soil along the lateral surface. From this arises a decreased value of pressure on the inferior base as this silo effect increases, i.e. for every increase in the ratio D/B, which is accounted for by the coefficient Nq .
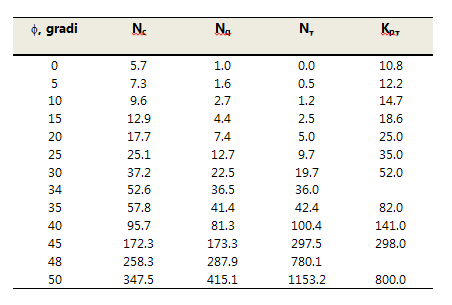
For soil with friction (φ) and cohesion (c), unit resistance Qp at the point is given by the expression:
Qp = c ´ Nc + γ ´ L ´ Nq
where:
γ = is unit weight of the soil;
L = length of pile;
Nc and Nq = are the bearing capacity factors including of the effect due to the shape (circular).
Vesic’s method
Vesic likens the problem of failure at the pile tip to that of the expansion of a cylindrical cavity immersed in a elastoplastic medium, so that even the compressibility of the medium is taken in account.
According to Vesic the bearing capacity coefficients Nq e Nc may be evaluated as shown:
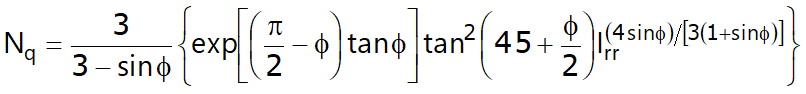
Reduced rigidity index Irr in the preceding expression is evaluated based on volumetric deformation εv.

Rigidity index is evaluated using tangential elasticity modulus G’ and the soil’s shear resistance. When soil is undrained or soil is in dense state, the term ev may be assumed to be zero thus rendering Irr=Ir.
Ir may be taken from the following table:
Terreno |
Ir |
Sand |
75-150 |
Silt |
50-75 |
Clay |
150-250 |
The coefficient Nc is evaluated as:
![]()
When φ = 0 (undrained condition):
![]()
Janbu’s method
Janbu evaluates Nq as follows: (The angle y is expressed in radians)
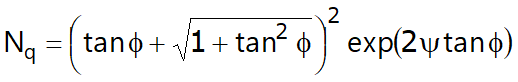
Nc may be obtained from (a) when φ > 0. Where φ = 0 use Nc = 5.74.
Hansen’s formula
Hansen’s formula is valid for all ratios D/B and so both for surface and deep foundations. However the author introduced a number of coefficients, in order to better reflect the actual behaviour of foundations. Without these there would be a too great increase in bearing capacity with increase in depth.
For values L/D < 1 :
|
|
Where φ = 0:
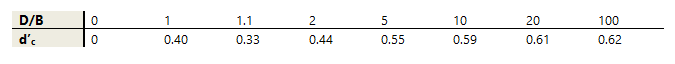
In the following, the expressions with (') are applicable when φ =0.
Form (shape) factor:
|
|
|
|
Depth factor:
|
|
|
|
|
© GeoStru