El método hiperbólico modificado representa un desarrollo del estudio de Chin (1970,1972,1983) que permite estimar el asiento de pilotes individuales a partir de la idea que el diagrama carga-asiento, por el cuerpo de un pilote y su base tenga un andar hiperbólico. Los valores de la carga última lateral (Qsu) y la resistencia de base última (Qbu) representan los términos asintóticos de la curva (figura a) (Terzaghi, 1943). Es posible agregar una representación del problema considerando la variación de la S/Q respecto al desplazamiento S (figura b).
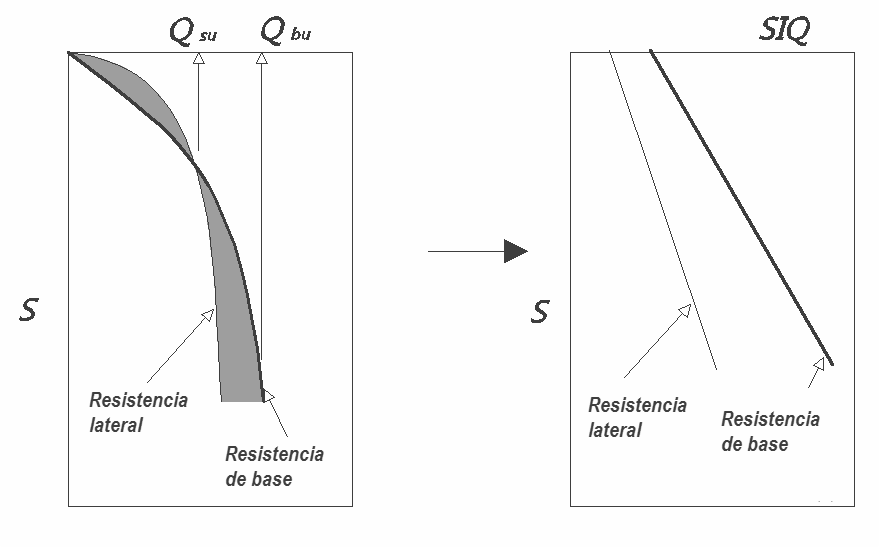
El estudio de Fleming ha demostrado que los desplazamientos totales estimados con el método de Chin eran disturbados por la reducción elástica del cuerpo del pilote por el cual sugirió un atécnica aplicada de la deformación elástica del pilote puede ser determinada sustrayendo la estima de Chin la reducción del pilote antes de diagramar la curva hiperbólica.
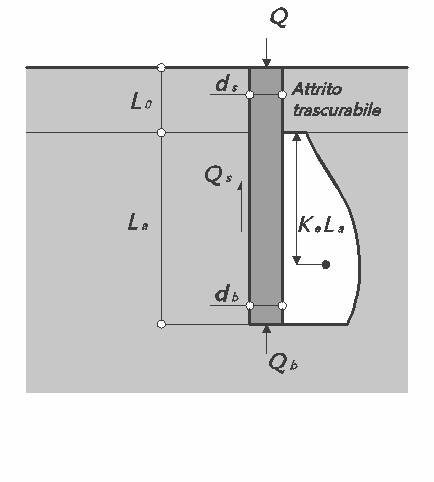
Considerando el esquema en figura la reducción elástica del pilote y de la carga aplicada Q en relación al rozamiento lateral último Qsu. En particular si Q≤Qsu la deformación elástica del cuerpo del pilote corresponde a la suma de la reducción elástica a lo largo de la zona de rozamiento nulo y aquel que se desarrolla en la parte activa del fusto:
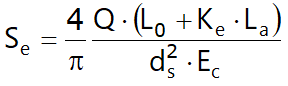
si en cambio se tiene Q>Qsu se tiene que considerar otra reducción a la parte activa del pilote que será agregada a la deformación elástica

Los parámetros de la fórmula son:
•ds=diámetro cabeza del pilote.
•Ec= módulo de elasticidad del material del pilote em el cual el valor puede ser obtenido por una interpretación lineal entre valores de Ec= 26(106) KN/m2 para hormigón con fuerza específica de 20 N/mm2 y el valor de Ec= 40(106) KN/m2 hormigón de 40 N/mm2.
•L0 = largo del pilote con rozamiento bajo o nulo.
•La= largo activo del pilote
•Ke= relación del largo equivalente al fusto del pilote con respecto al largo activo La. Se puede considerar un valor de 0.5 cuando se tiene un rozamiento que sen desarrolla uniformemente a lo largo La o bien cuando el pilote va introducido en arena o grava. Para pilotes en creta caracterizados por un esfuerzo que crece en profundidad se puede utilizar un valor de 0.45.
El desplazamiento del pilote rígido puede ser calculado sabiendo que la suma del rozamiento lateral y de la resistencia de base corresponden al total aplicado a la cabeza del pilote.
![]()
Considerando el pilote rígido el desplazamiento total en cabeza es igual a aquel que se obtiene a lo largo del fusto es igual a aquel medido en la base del pilote:
![]()
Del gráfico lineal se puede ver que el desplazamiento a lo largo del fusto del pilote puede ser calculado así:
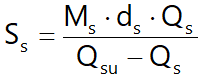
En el cual
•Ms= factor sin unidad de medida de flexibilidad terreno/fusto.
•ds0= diámetro cabeza
•Qs= Rozamiento
•Qsu= Rozamiento último determinado con el método estático (condición con drenaje)
La ecuación del desplazamiento a la base del pilote obtiene de Fleming:

donde
•db=diámetro de la base del pilote.
•Qb=: resistencia a la base.
•Qbu= resistencia última a la base.
•Eb= módulo de corte correspondiente a Qbu/4
En fin poniendo la condición de igualdad Ss=Sb y considerando la carga total aplicada Q se obtiene el desplazamiento total de un pilote rígido considerando solo los valores positivos de la relación:

En el cual las variables se definen así:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
El desplazamiento del pilote comprende el componente de desplazamiento rígido y aquella de reducción elástica.
El módulo elástico del terreno Eb por debajo de la base del pilote es vinculada a las características del terreno y es fuertemente influenciado por la técnica de construcción pilote. Fleming sostiene que es aconsejable que esta parámetro de proyecto sea determinado por un conjunto de ensayo en los cuales los pilotes son cargados hasta el punto en el cual es mobilizada una importante cota de la resistencia de punta. En ausencia de estos datos se puede elegir, con cautela el valor Eb del range de valores relativos al tipo de terreno y a al técnica de construcción del pilote.
•Pilotes barrenados en arcilla
Consistencia arcilla |
Eb [kN/m2] |
Muy suave |
< 3000 |
Suave |
3000 – 6000 |
Compacta |
6000 – 15000 |
Consistente |
15000 – 25000 |
Muy consistente |
25000 – 40000 |
Dura |
> 40000 |
•Pilotes barrenados en arena o grava
Tipo terreno |
Eb [kN/m2] |
Batante suelto |
< 15000 |
Suelto |
15000 – 30000 |
Mediamente sciolto |
30000 – 100000 |
Compacto |
100000 – 200000 |
Bastante compacto |
> 200000 |
•Pilotes barrenados en margas y esquistos
Tipo terreno |
Eb [kN/m2] |
íntegro |
150000 – 200000 |
Relativamente alterado |
80000 – 150000 |
Alterado |
50000 – 80000 |
Muy Alterado |
10000 – 50000 |
•Pilotes barrenados en yeso
Tipo de yeso |
Eb [kN/m2] |
Fisurado |
< 100000 |
Con fisuras > 3 mm |
100000 – 200000 |
Con fisuras < 3 mm |
150000 – 250000 |
Discontinuidad cerrada |
> 250000 |
Si el pilote es de base alargada los valores de la tabla tiene que ser multiplicados por un factor 1.5. Los factores de flexibilidad asta/terreno Ms es un valor sin unidad de medida comprendido entre 0.001 e 0.0015. Su valor no parece ser influenciado por el tipo de pilote ni del tipo de terreno.
© <%AUTHOR%