Nel caso in cui un palo è soggetto a carico orizzontale, occorre verificare che il palo rimanga in condizioni di sicurezza anche rispetto a tali condizioni carico.
Nelle verifiche a carico trasversale viene applicata la teoria sviluppata da Broms per mezzo puramente coesivo e per mezzo incoerente nei casi di palo incastrato in testa o con possibilità di rotazione (libero).
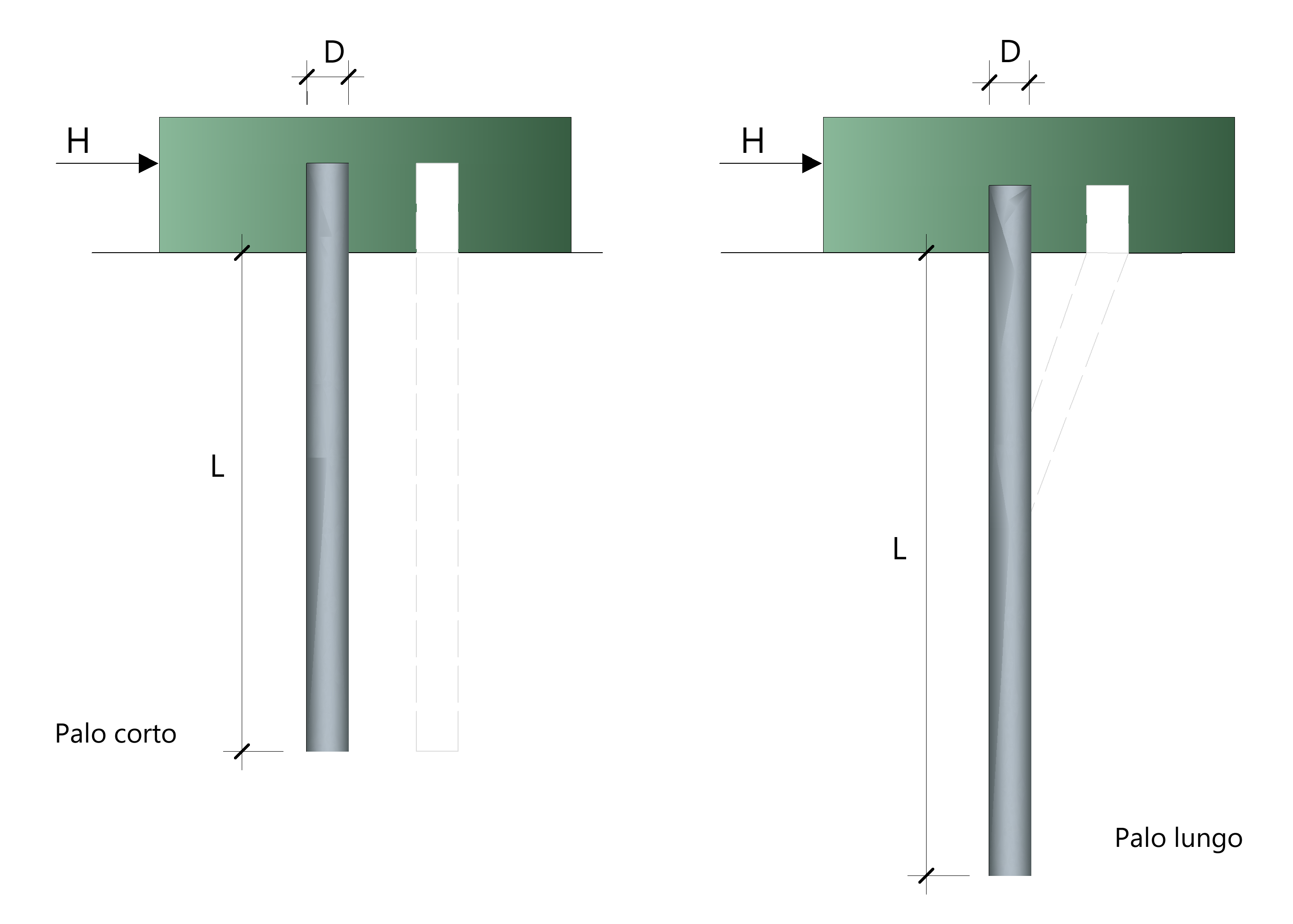
Palo libero di ruotare
In questa ipotesi rientrano due possibili meccanismi di rottura evidenziati in figura.
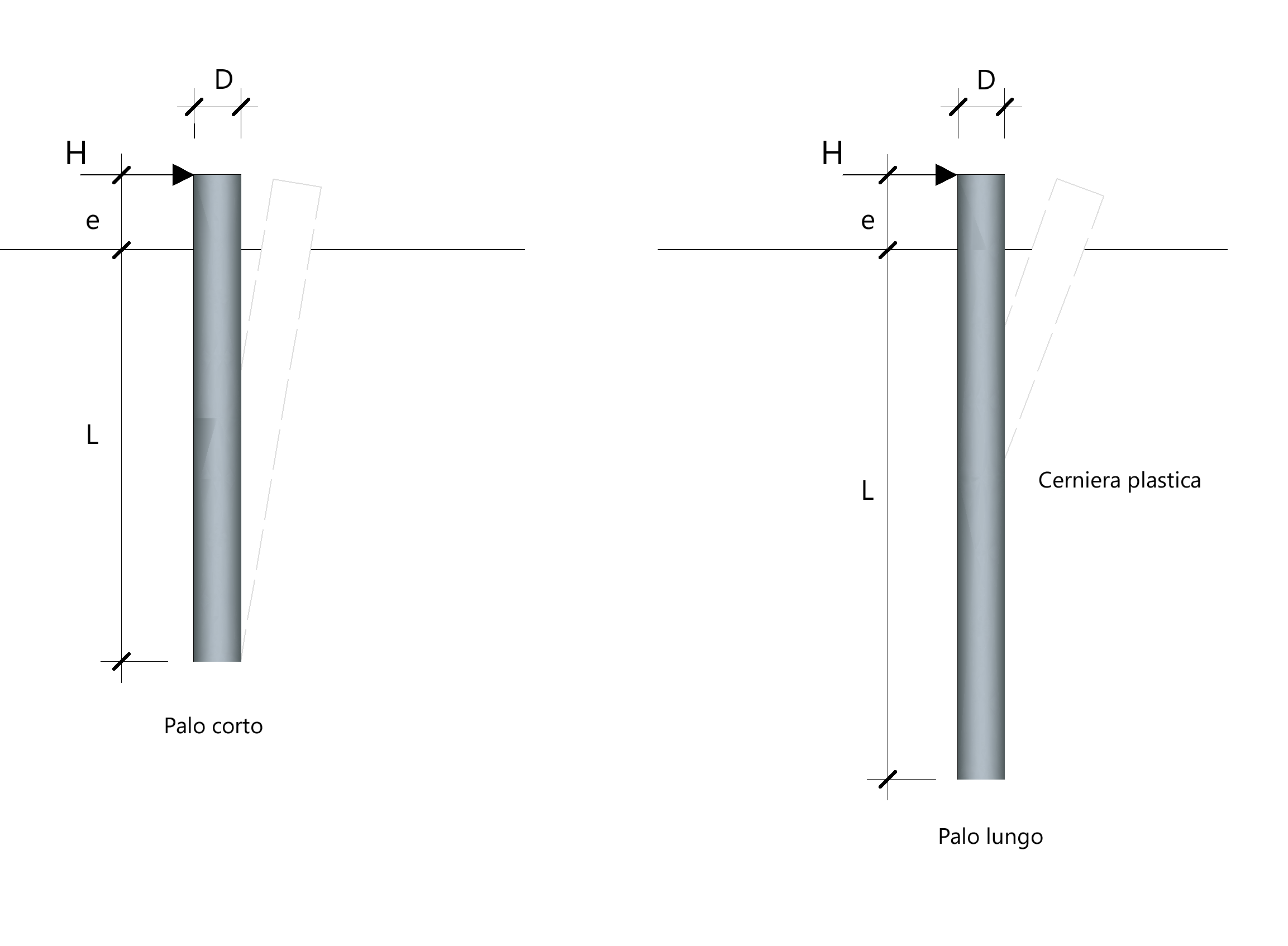
I due meccanismi di collasso corrispondono, rispettivamente, ad un moto rigido di rotazione attorno ad un suo punto (palo corto) oppure ad un moto di rotazione relativa intorno ad una cerniera plastica.
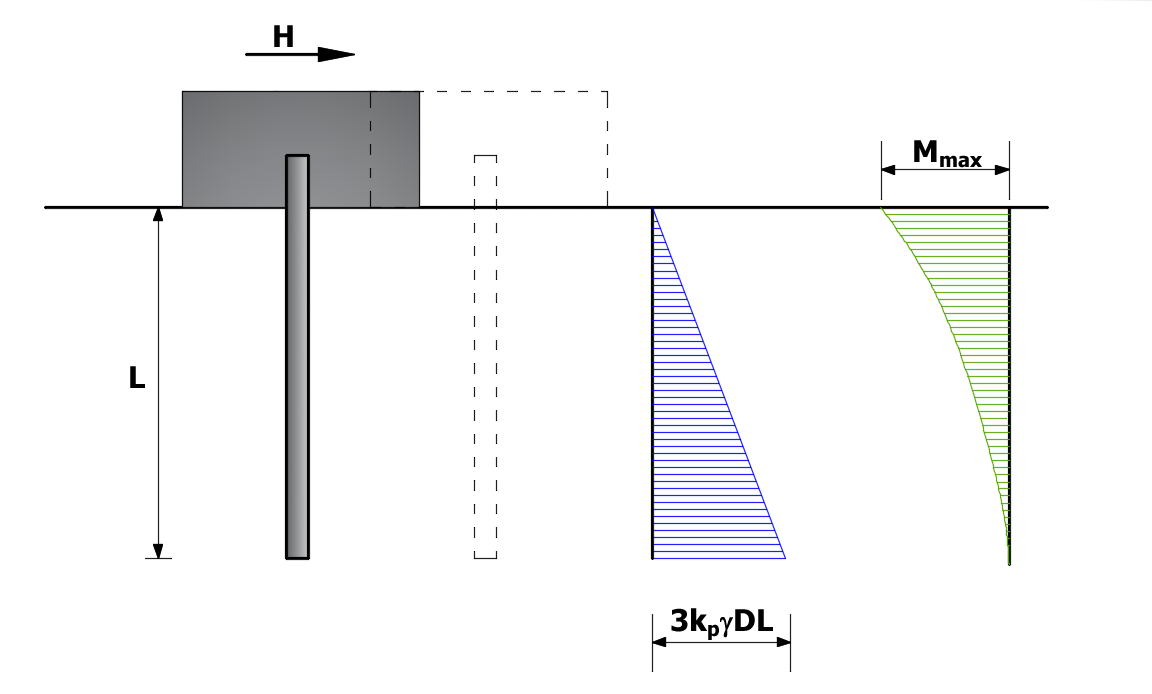
Per palo rigido (palo corto), l'equazione di equilibrio, in condizione ultima, dei momenti rispetto al piede del palo, è data dalla seguente espressione:
da cui:
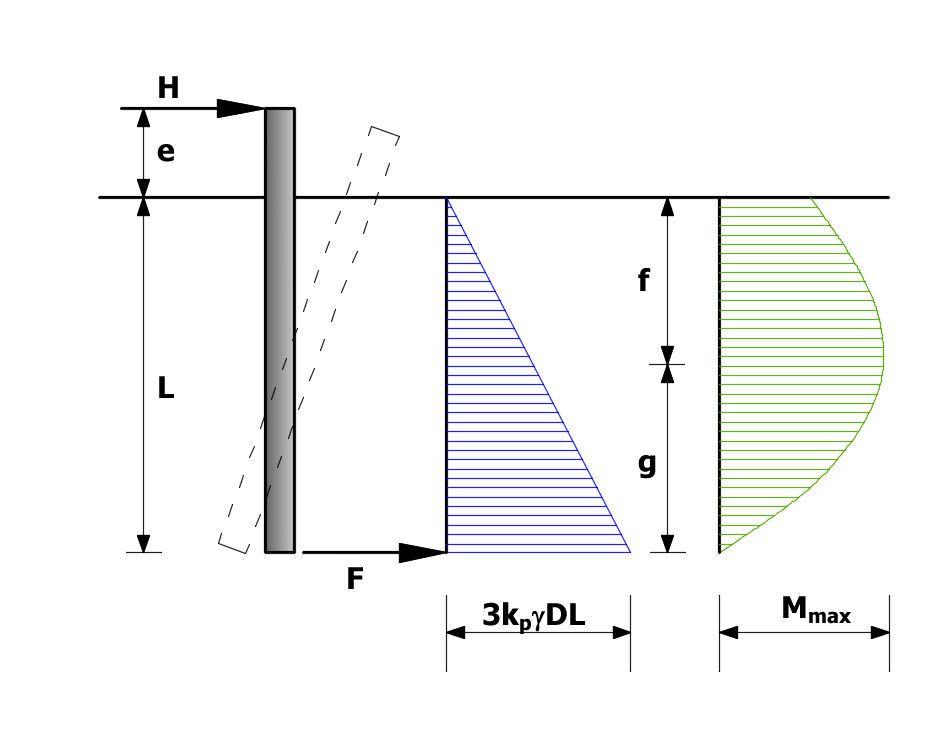
Palo libero di ruotare in testa, terreno incoerente, palo corto.
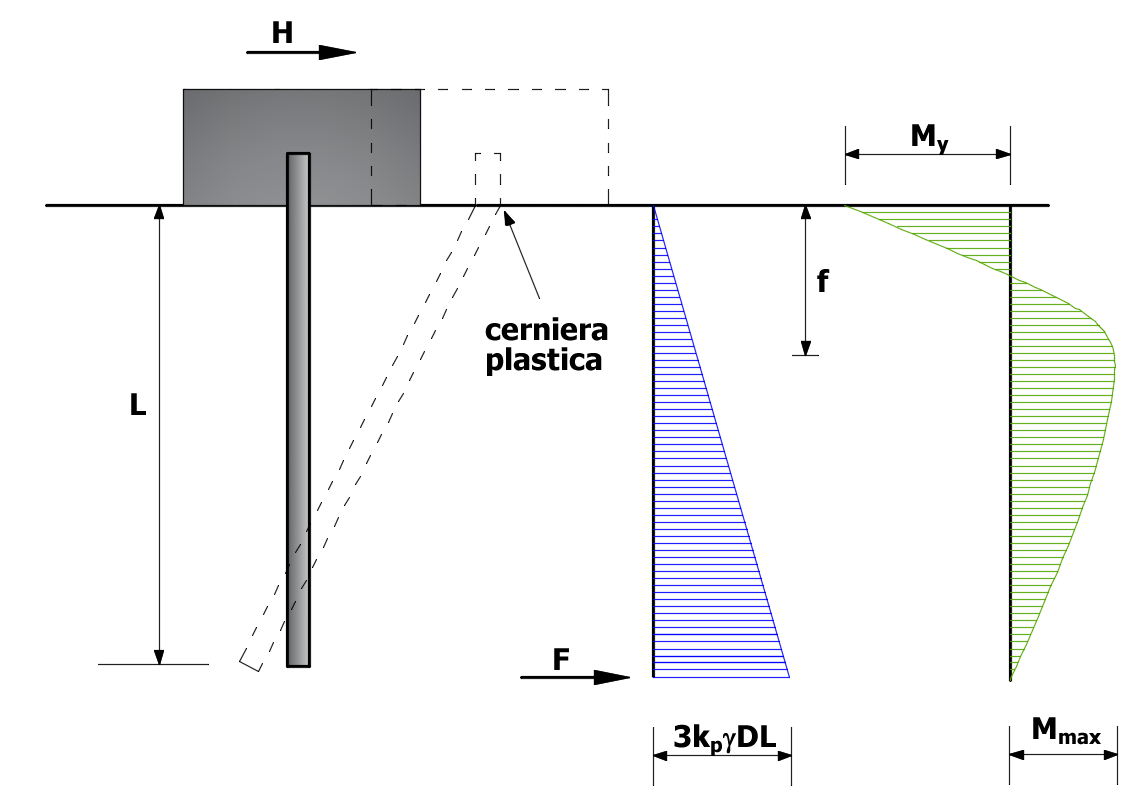
Occorre però verificare che il momento massimo, legato al taglio, sia minore del momento di plasticizzazione Mmax ≤ My. Il momento massimo si stima nel punto di taglio nullo (f):
My = momento di plasticizzazione del palo
Se il palo è flessibile (palo lungo) si verificherà che Mmax > My. Uguagliando l'espresssione di Mmax con My si ottiene (nell'espressione seguente viene trascurata l'eccentricità):
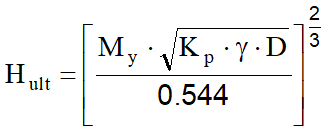
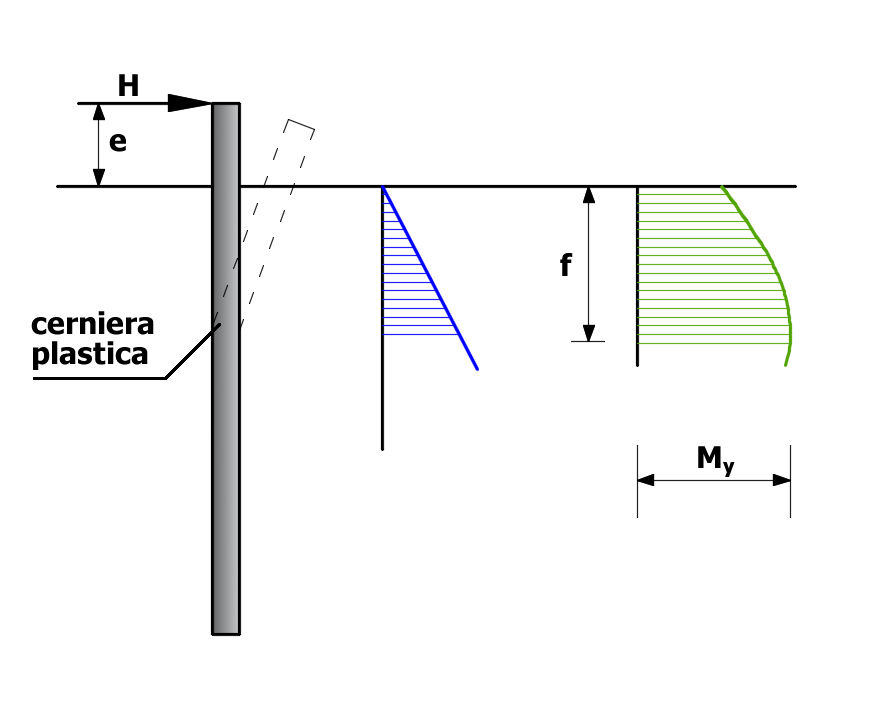
Palo libero di ruotare in testa, terreno incoerente, palo lungo.
Il coefficiente Kp , nell'ipotesi di terreno incoerente, si assume pari a quello di spinta passiva di Rankine:
Palo incastrato
Quando il palo è incastrato in testa i meccanismi di rottura possibili sono:
Per palo rigido (palo corto), dall'equazione di equilibrio alla traslazione orizzontale risulta:
Anche in questo caso occorre verificare che Mmax ≤ My, il momento massimo questa volta si verifica nell'incastro e vale:
Palo impedito di ruotare in testa, terreni incoerenti, palo corto
Possono verificarsi due casi, palo intermedio con formazione di una sola cerniera plastica all'attacco con la struttura di fondazione oppure palo lungo con la formazione di una seconda cerniera plastica lungo il fusto.
Nel primo caso, dall'equilibrio della traslazione si ricava:
Imponendo l'equilibrio alla rotazione attorno alla cerniera plastica si ottiene:
Palo impedito di ruotare in testa, terreni incoerenti, palo intermedio
Nel caso di palo lungo, l'equilibrio alla traslazione del tratto di palo tra due cerniere plastiche, fornisce:
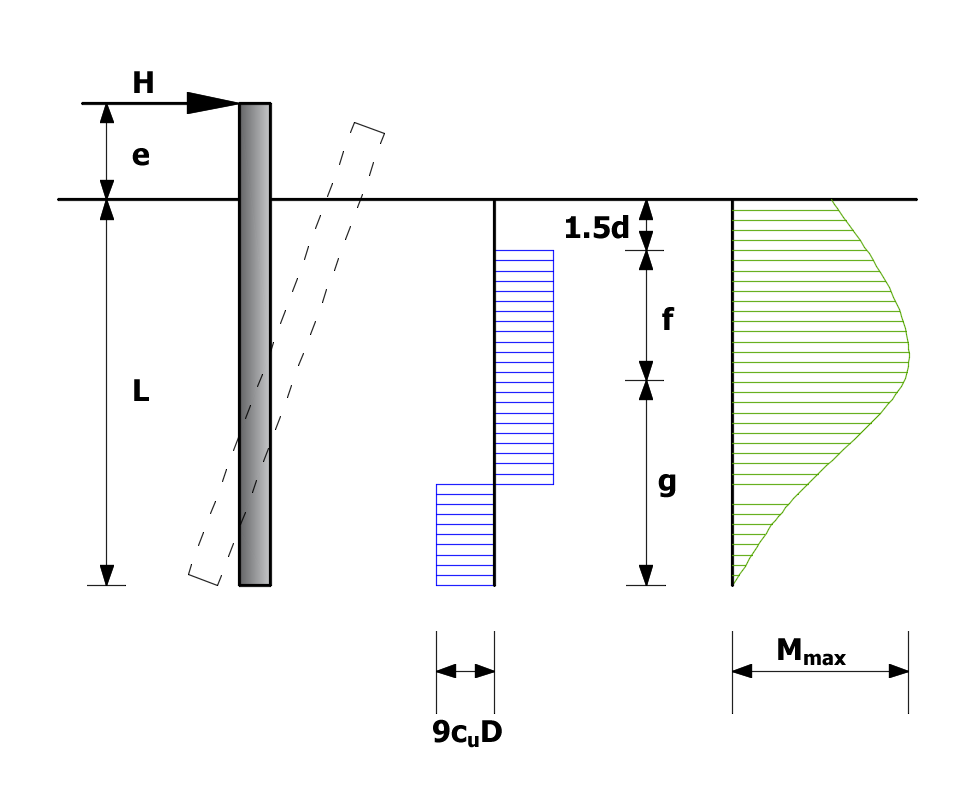
Come a solito f rappresenta il punto lungo il palo in cui il taglio si annulla, si ricava quindi:
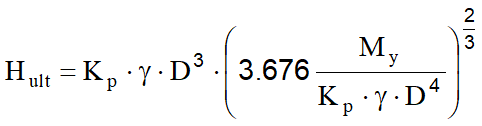
Palo impedito di ruotare in testa, terreni incoerenti, palo lungo
Per terreni puramente coesivi, Broms analizza sempre gli stessi meccanismi di rottura, ma valuta la reazione del terreno in condizioni non drenate. Risultano, pertanto le seguenti espressioni.
Palo libero di ruotare
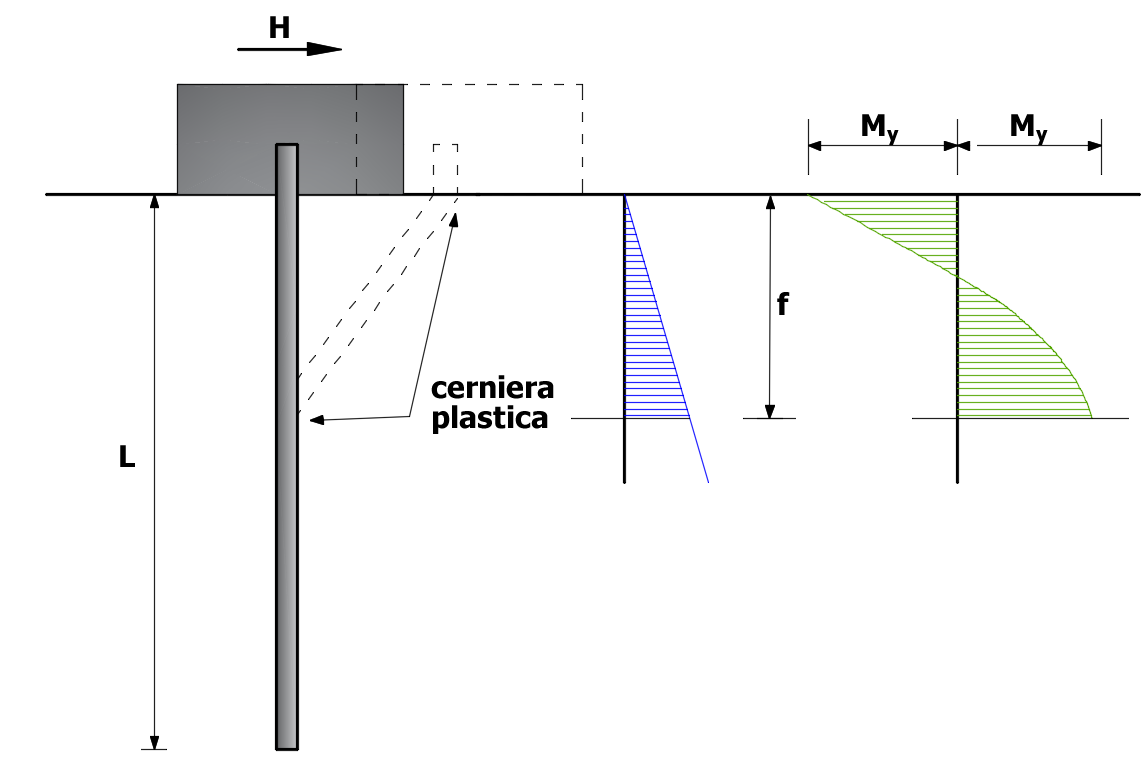
Se in ogni sezione del palo si verifica la disuguaglianza Mmax≤ My allora il palo viene definito corto, ovvero il terreno si plasticizza prima del palo. Alla profondità z= 1.5d+f, il momento è massimo e quindi in tale sezione il taglio sarà nullo. Dall'equazione di equilibrio alla traslazione del tronco superiore del palo si ricava il valore di:
L'equazione di equilibrio alla rotazione dell'intero palo rispetto al punto di momento massimo fornisce invece:
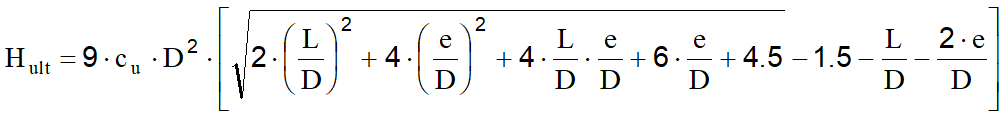
Il momento massimo assume il seguente valore:
Palo libero di ruotare in testa, terreno coesivo, palo corto.
Nel caso in cui Mmax> My , il palo in esame è definito lungo. L'equazione di equilibrio alla traslazione del tronco superiore del palo sarà ancora valida:
Dall'equazione di equilibrio alla rotazione del troco di palo si ricava:
Combinando le due equazioni precedenti si ricava:
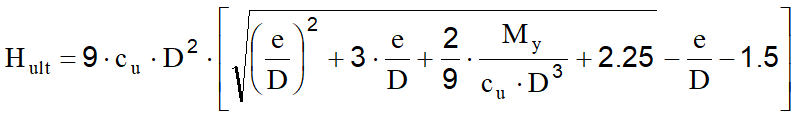
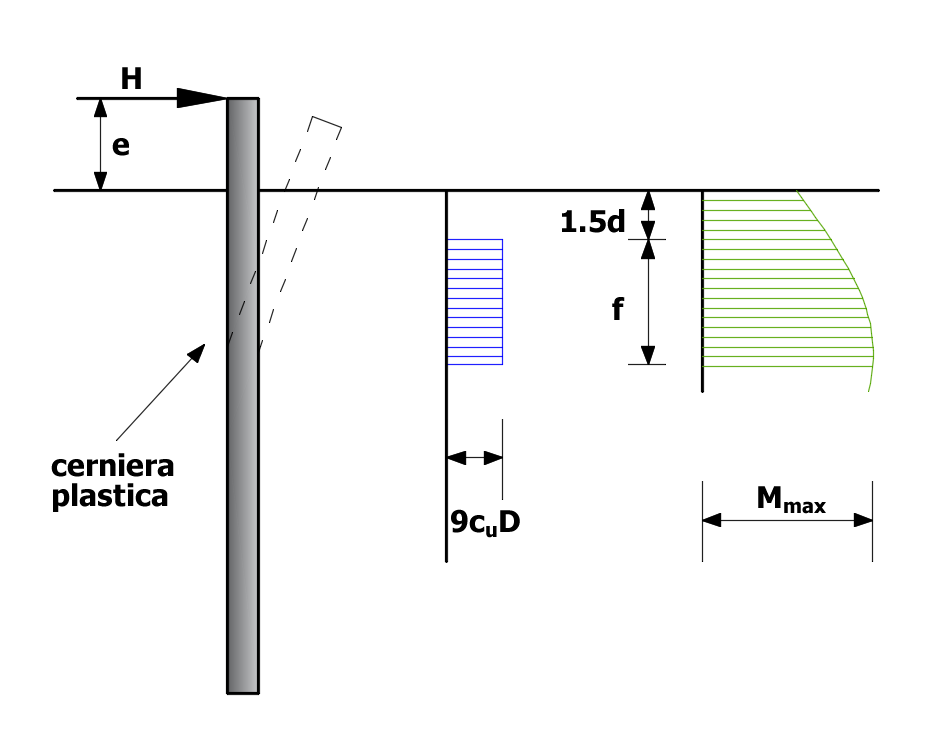
Palo libero di ruotare in testa, terreno coesivo, palo lungo.
Palo rigido incastrato
Come per i terreni incoerenti, anche per i terreni coesivi i meccanismi di rottura del palo possomo essere identificati come palo corto, intermedio e lungo.
Per il palo corto l'equazione di equilibrio alla traslazione del palo fornisce:
La condizione da rispettare è che Mmax≤ My dove :
Sostituendo Hult nell'espressione precededente si ottiene:
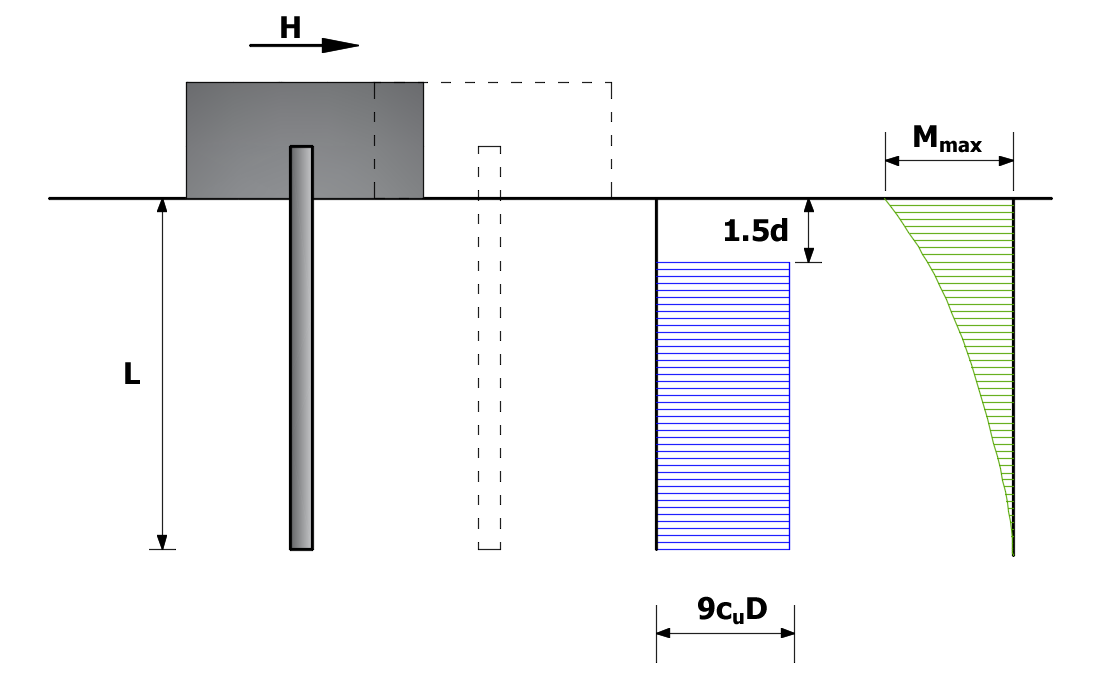
Palo impedito di ruotare in testa, terreni coesivi, palo corto
Nel caso di palo intermedio si ha la formazione di una sola cerniera plastica nella sezione di collegamento della struttura di fondazione. Dall'equilibrio alla traslazione orizzontale del tronco di palo della sezione di momento massimo e dalla condizione di equilibrio alla rotazione attorno al punto in cui si forma la cerniera plastica, si ricava:
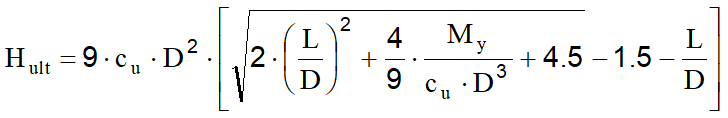
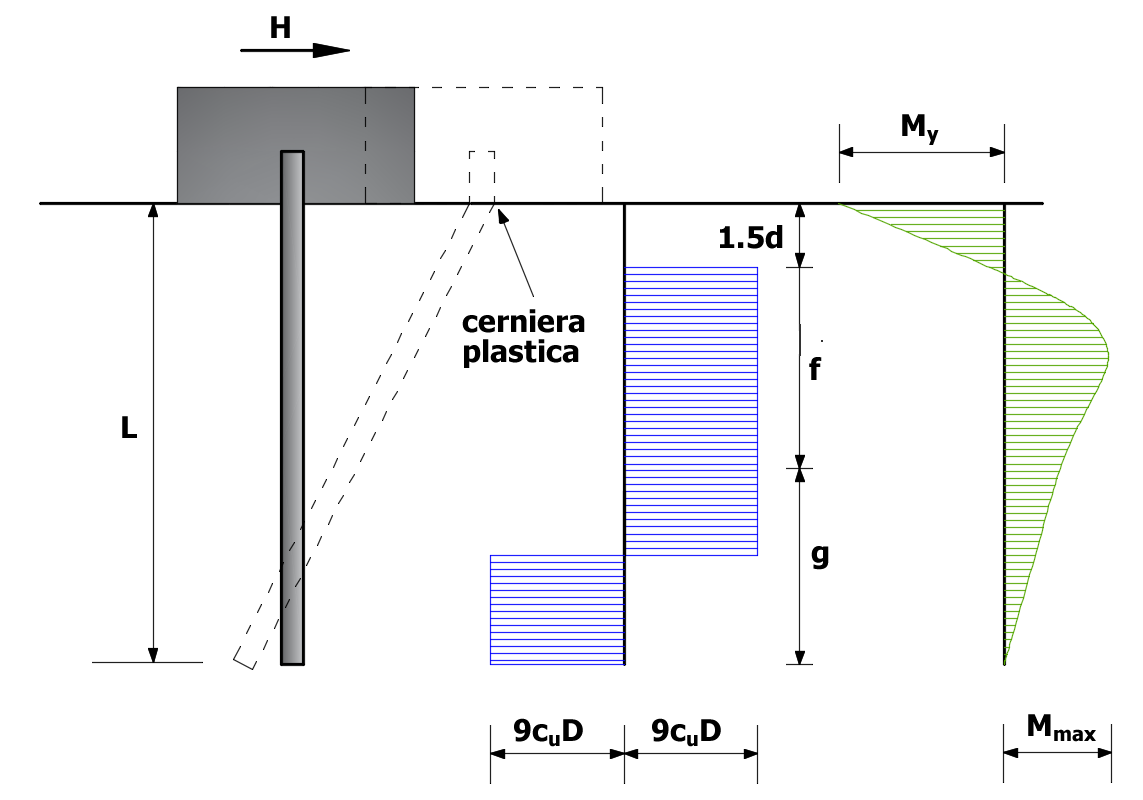
Palo impedito di ruotare in testa, terreni coesivi, palo intermedio
Nel caso di palo lungo il massimo momento lungo il fusto si verifica nella sezione a profondità 1.5D+f, in tale sezione il momento massimo uguagli ail momento di plasticizzazione My formando in tal caso una seconda cernier plastica.
Dall'equilibrio alla rotazione del tratto di palo compreso tra due cerniere plastiche si ottiene:
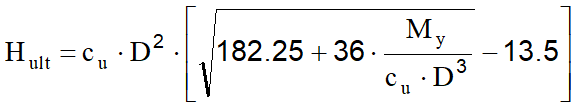
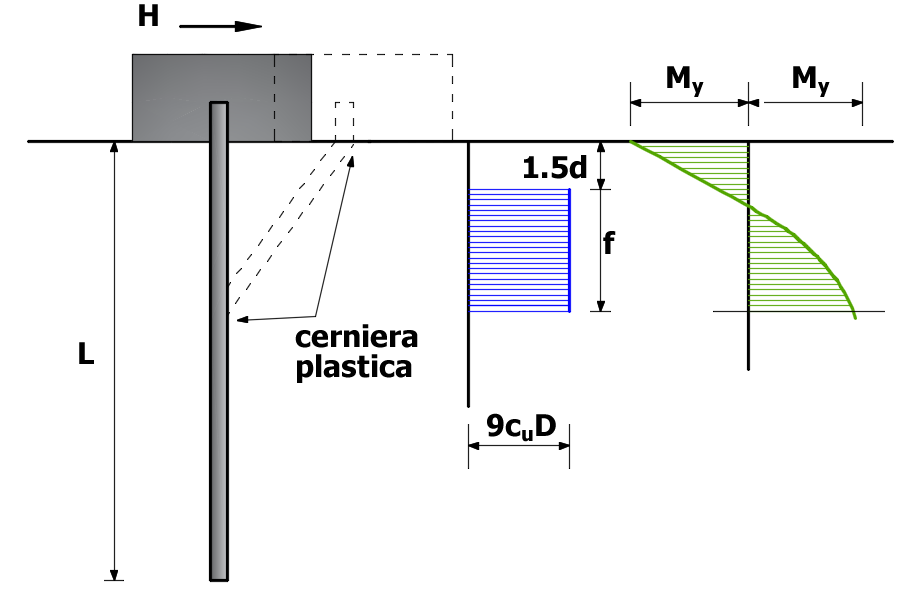
Palo impedito di ruotare in testa, terreni coesivi, palo lungo
© GeoStru