Il metodo iperbolico modificato rappresenta uno sviluppo dello studio di Chin (1970, 1972, 1983) che consente di stimare il cedimento di pali singoli partendo dall’idea che il diagramma carico-cedimento, per il corpo di un palo e la sua base, abbia un andamento iperbolico. I valori del carico ultimo laterale (Qsu) e della resistenza di base ultima (Qbu) rappresentano i termini asintotici della curva (figura a) (Terzaghi, 1943). Partendo da queste ipotesi è possibile giungere ad una rappresentazione linearizzata del problema considerando la variazione della quantità S/Q rispetto allo spostamento S (figura b).
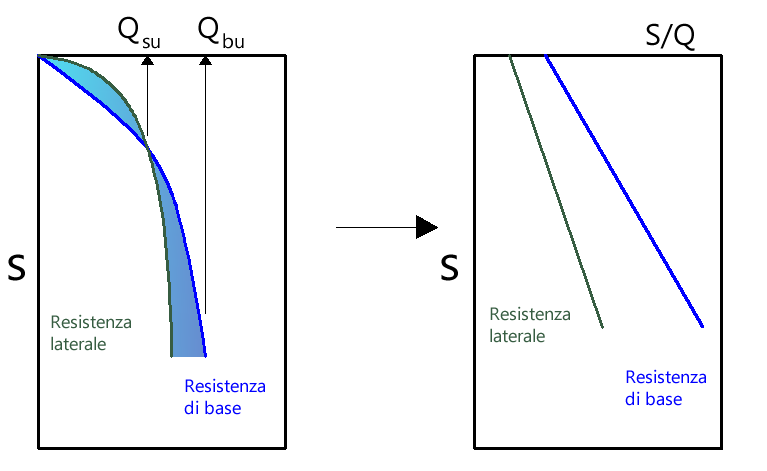
Lo studio di Fleming ha dimostrato che gli spostamenti totali stimati col metodo di Chin erano distorti dall’accorciamento elastico del corpo del palo e suggerì una tecnica semplificata per la quale la deformazione elastica del palo può essere determinata, con sufficiente accuratezza, sottraendo alla stima del cedimento di Chin l’accorciamento del palo.
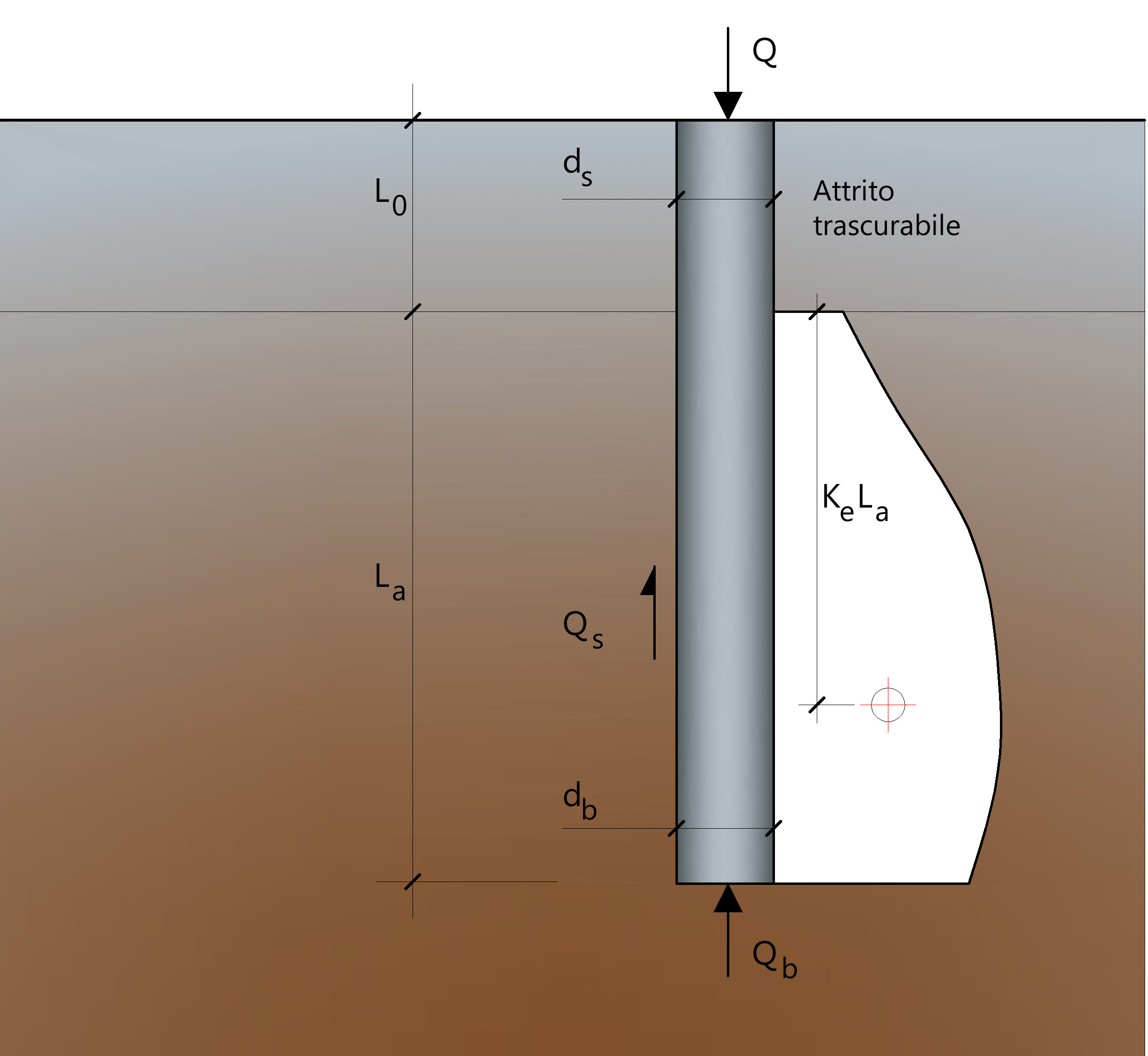
Considerando lo schema in figura l’accorciamento elastico del palo dipende dal carico applicato Q in rapporto all’attrito laterale ultimo Qsu. In particolare se Q≤Qsu la deformazione elastica del corpo del palo corrisponde alla somma dell’accorciamento elastico lungo la zona ad attrito basso o nullo e quello che si sviluppa lungo la parte attiva del fusto:
![]()
Se, invece, si ha che Q>Qsu bisogna considerare un ulteriore accorciamento legato alla parte attiva del palo che deve essere aggiunta alla deformazione elastica:
![]()
I parametri della formula sono:
ds= diametro testa del palo.
Ec= modulo di elasticità del materiale del palo il cui valore può essere ricavato da una interpolazione lineare tra i valori di
Ec= 26(106) KN/m2 per calcestruzzo con forza specifica di 20 N/mm2 e il valore di Ec= 40(106) KN/m2per calcestruzzo da 40 N/mm2.
L0 = lunghezza del palo ad attrito basso o nullo.
La= lunghezza attiva del palo.
Ke= rapporto della lunghezza equivalente del fusto del palo rispetto alla lunghezza attiva La . Si può considerare un valore di 0.5
quando si ha un attrito che si sviluppa uniformemente lungo La oppure quando il palo è inserito in sabbia o ghiaia. Per pali in argilla caratterizzati da uno sforzo che cresce in profondità si può usare un valore di 0.45.
Lo spostamento del palo rigido può essere calcolato sapendo che la somma dell’attrito laterale e della resistenza di base corrisponde al carico totale applicato alla testa del palo.
![]()
Considerando il palo rigido lo spostamento totale in testa è uguale a quello che si ottiene lungo il fusto ed è uguale a quello misurato alla base del palo:
![]()
Dal grafico linearizzato si può vedere che lo spostamento lungo il fusto del palo può essere calcolato come:
![]()
In cui:
Ms= fattore adimensionale di flessibilità terreno/fusto.
ds0= diametro in testa al palo.
Qs= attrito.
Qsu= attrito ultimo determinato col metodo statico (condizione drenata)
L’equazione dello spostamento alla base del palo ricavata da Fleming è:
![]()
dove:
db= diametro della base del palo.
Qb= resistenza alla base.
Qbu= resistenza ultima alla base
Eb= modulo di taglio corrispondente a Qbu/4
Infine, ponendo la condizione di uguaglianza Ss=Sb e considerando il carico totale applicato Q si ottiene lo spostamento totale di un palo rigido considerando solo i valori positivi della relazione:
![]()
In cui le variabili sono così definite:
![]()
![]()
![]()
dove:
![]()
![]()
![]()
![]()
![]()
Lo spostamento complessivo del palo comprende la componente di spostamento rigido e quella di accorciamento elastico.
Il modulo elastico del terreno Eb al di sotto della base del palo è legato alle caratteristiche del terreno ed è fortemente influenzato dalla tecnica di costruzione del palo. Fleming sostiene che è consigliabile che questo parametro di progetto sia determinato da un insieme accurato di prove in cui i pali sono caricati fino al punto punto in cui viene mobilitata una sostanziale quota della resistenza di punta. In mancanza di questi dati si può scegliere, cautelativamente, il valore di Eb da range di valori relativi al tipo di terreno e alla tecnica di costruzione del palo.

Se il palo è a base allargata i valori delle tabelle devono essere moltiplicati per un fattore 1.5. Il fattore di flessibilità asta/terreno Ms è un valore adimensionale compreso tra 0.001 e 0.0015. Il suo valore non sembra essere influenzato dal tipo di palo né dal tipo di terreno.
© GeoStru