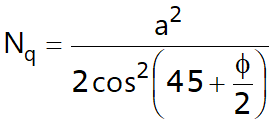Formula di Terzaghi
La soluzione proposta da Terzaghi assume che il terreno esistente al di sopra della profondità raggiunta dalla punta del palo possa essere sostituito da un sovraccarico equivalente pari alla tensione verticale efficace (trascurando pertanto il fatto che l’interazione tra palo e terreno di fondazione possa modificare tale valore) e riconduce l’analisi al problema di capacità portante di una fondazione superficiale (vedi immagine).
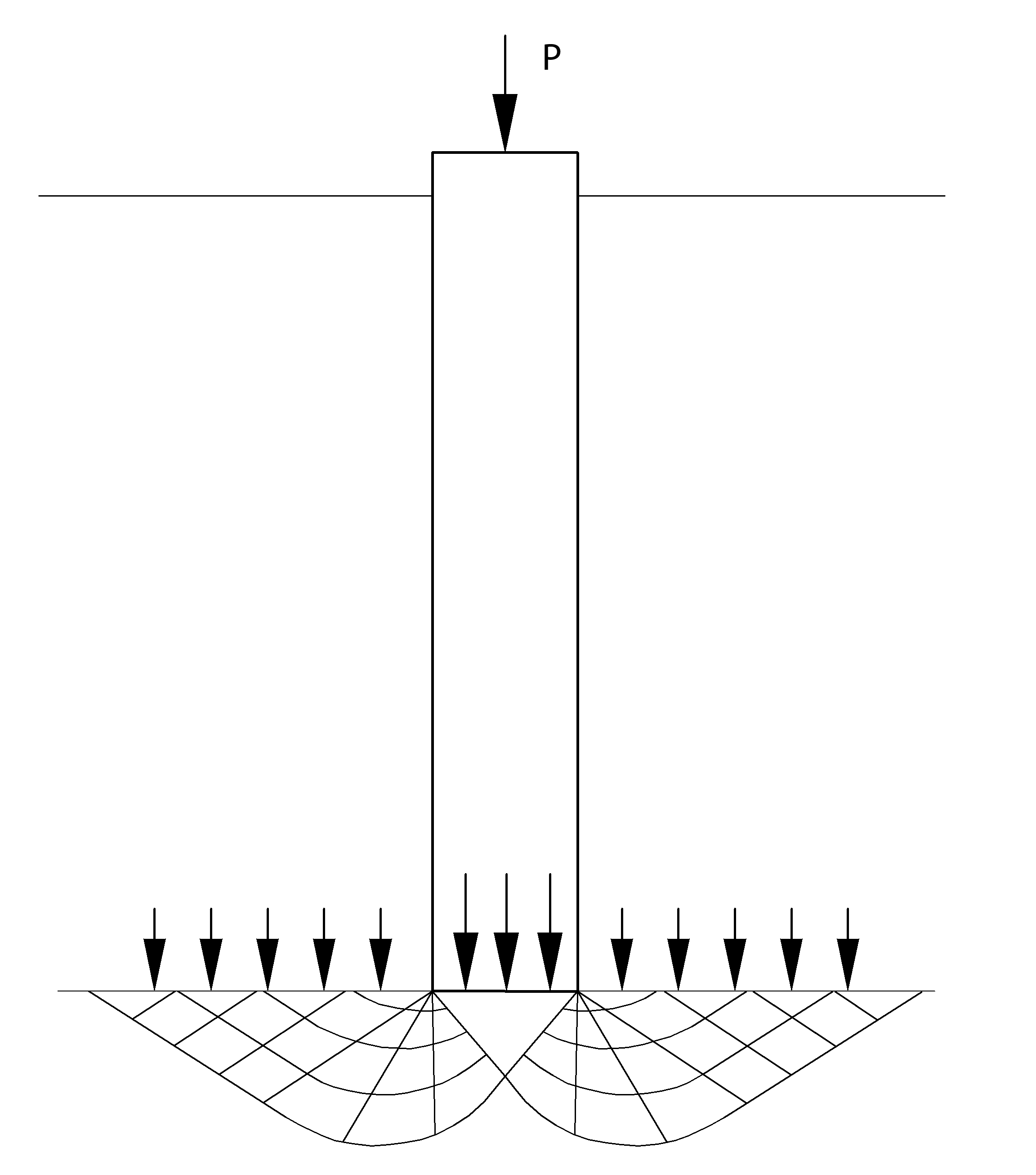
Meccanismo di rottura di Terzaghi
La formula di Terzaghi può essere scritta:
![]()
dove:
|
|
|
|
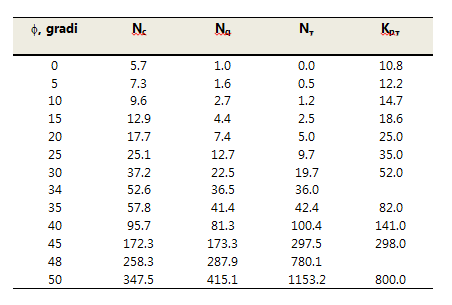
I coefficienti di portata che compaiono nella formula di Terzaghi sono riportati in tabella. Terzaghi non ha mai spiegato molto chiaramente come ha ricavato il coefficiente Kpg utilizzato per il calcolo di Nγ.
Metodo di Berezantzev
Fondamentalmente Berezantzev fa riferimento ad una superficie di scorrimento “alla Terzaghi” che si arresta sul piano di posa (punta del palo); tuttavia egli considera che il cilindro di terreno coassiale al palo ed avente diametro pari all’estensione in sezione della superficie di scorrimento, sia in parte “sostenuto” per azione tangenziale dal rimanente terreno lungo la superficie laterale. Ne consegue un valore della pressione alla base inferiore a γD, è tanto minore quanto più questo “effetto silo” è marcato, cioè quanto più grande è il rapporto D/B; di ciò tiene conto il coefficiente Nq, che quindi è funzione decrescente di D/B.
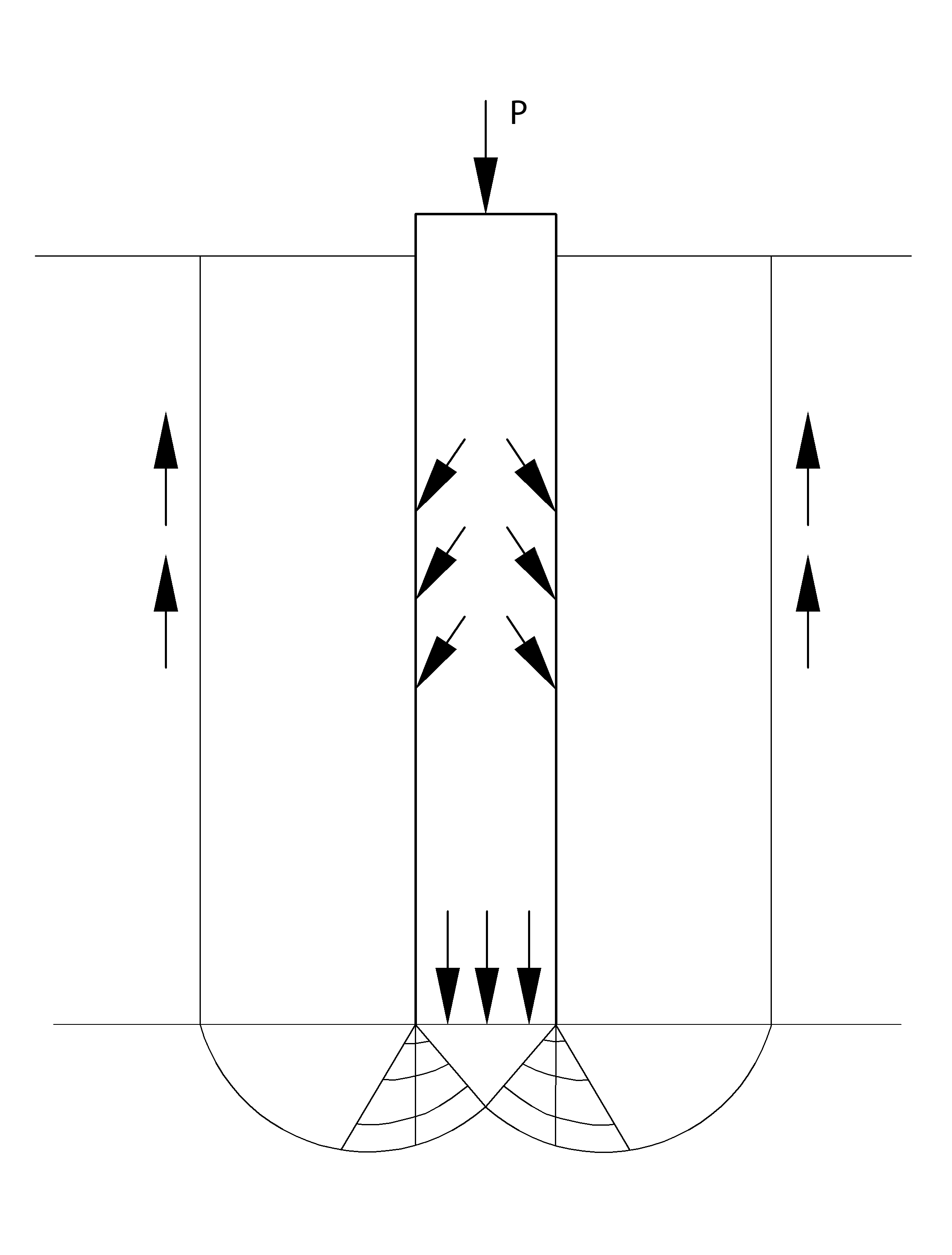
Meccanismo di rottura secondo Berezantzev
La resistenza unitaria Qp alla punta, per il caso di terreno dotato di attrito (φ) e di coesione (c), è data dall'espressione:
![]()
avendo indicato con:
γ = peso unità di volume del terreno;
L = lunghezza del palo;
Nc e Nq = sono i fattori di capacità portante già comprensivi dell'effetto forma (circolare).
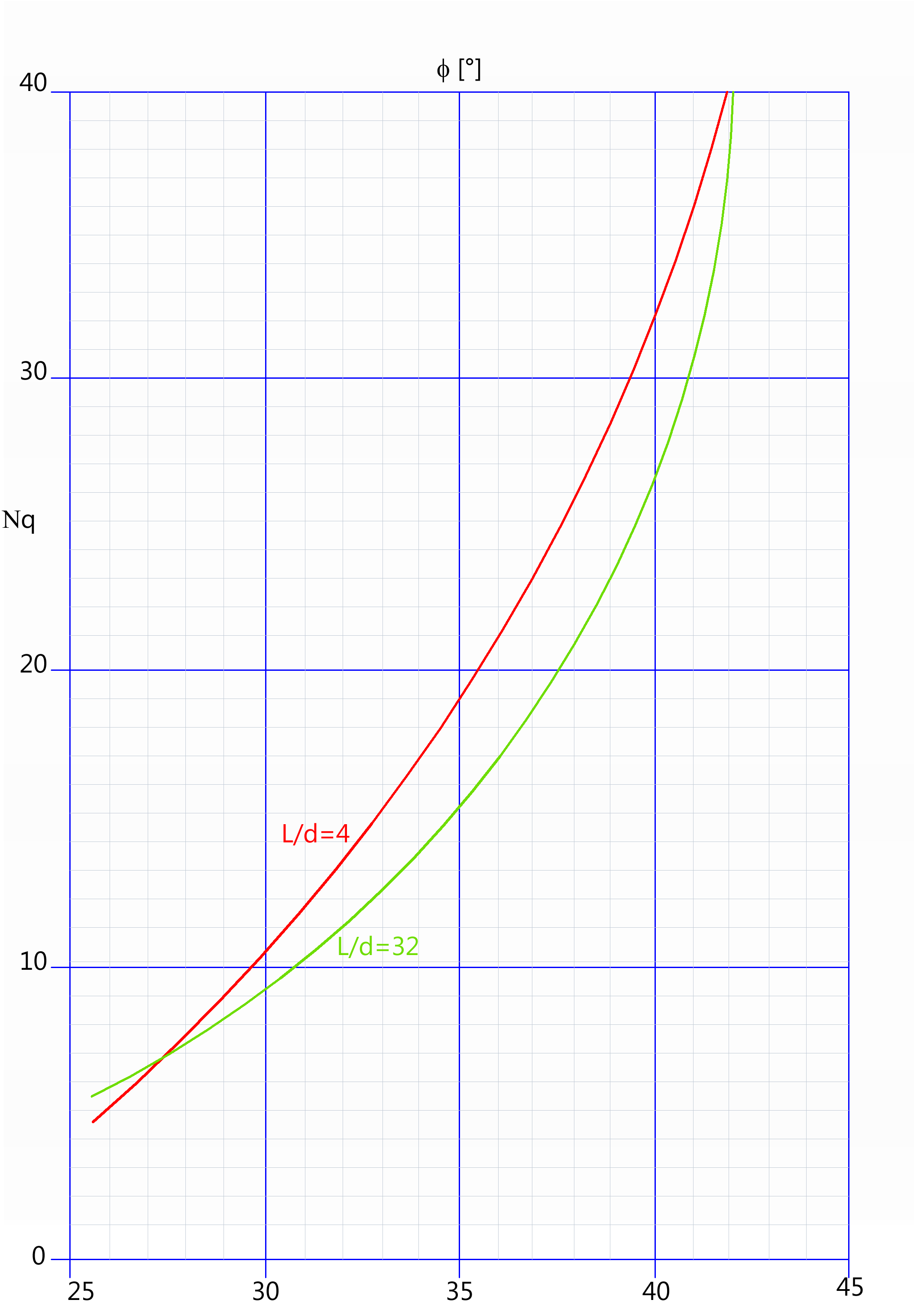
Metodo di Berezantzev (1965), coefficiente ridotto.
Per calcolare il fattore di capacità portante dovuto al sovraccarico, nel caso di terreni incoerenti e pali di grosso diametro, puo' essere utilizzata la seguente relazione:
![]()
Metodo di Vesic
Vesic ha assimilato il problema della rottura intorno alla punta del palo a quello di espansione di una cavità cilindrica in mezzo elasto-plastico, in modo da tener conto anche della compressibilità del mezzo.
Secondo Vesic i coefficienti di capacità portante Nq e Nc si possono calcolare come segue:
![]()
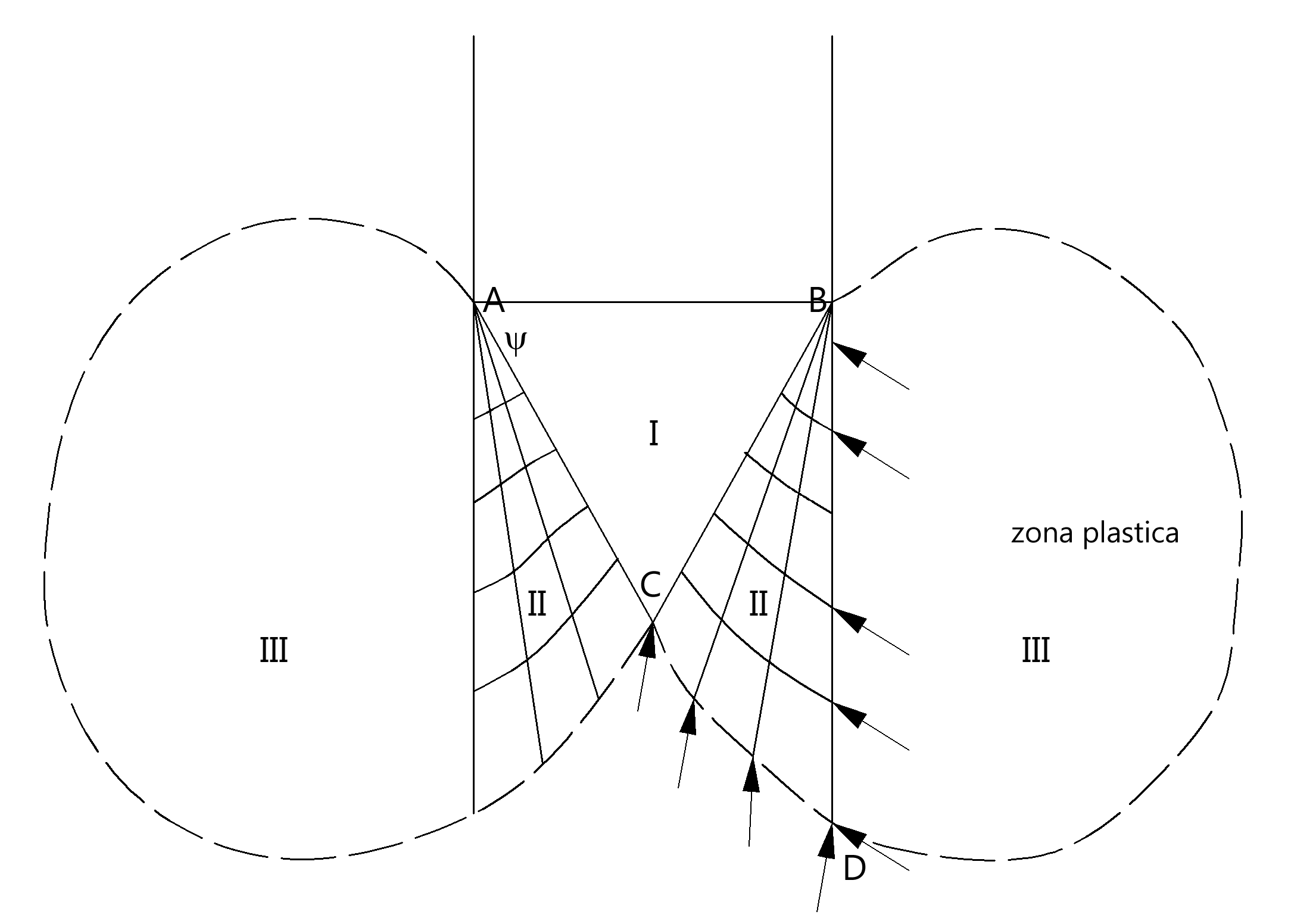
Meccanismo di rottura alla punta secondo Vesic
L’indice di rigidezza ridotto Irr nella precedente espressione viene calcolato a partire dalla deformazione volumetrica εv:
![]()
L’indice di rigidezza Ir si calcola utilizzando il modulo di elasticità tangenziale G’ e la resistenza a taglio t del terreno. Quando si hanno condizioni non drenate o il suolo il suolo si trova in uno stato addensato, il termine εv può essere assunto pari a zero e si ottiene Irr=Ir.
E’ possibile fare una stima di Ir con i valori seguenti:

Il termine Nc della capacità portante viene calcolato:
![]()
Quando ϕ=0 (condizioni non drenate):
![]()
Metodo di Janbu
Janbu calcola Nq (con l’angolo ψ espresso in radianti) come segue:
![]()
Nc si può ricavare dalla (a) quando ϕ> 0.
Per ϕ = 0 si usa Nc = 5.74
Formula di Hansen
La formula di Hansen vale per qualsiasi rapporto D/B, quindi sia per fondazioni superficiali che profonde, ma lo stesso autore introdusse dei coefficienti per meglio interpretare il comportamento reale della fondazione, senza di essi, infatti, si avrebbe un aumento troppo forte del carico limite con la profondità.
Per valori L/D>1:
|
|
Nel caso ϕ = 0:
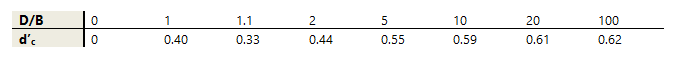
Nei fattori seguenti le espressioni con apici (') valgono quando ϕ = 0.
Fattore di forma:
|
|
|
|
Fattore di profondità:
|
|
|
|
|
© GeoStru