<< Click to Display Table of Contents >> Navigation:  Eurocode 7 - Application to superficial foundations - NF P94-261 > Bearing capacity > 2. Calculation of the net resistance of the ground > 2.5 - Calculation of coefficients iδ and iβ

2.5.1 - Preamble to the calculation of bearing reduction coefficients

 

The calculation of the coefficients iδ and iβ is independent of the in situ tests used (pressiometric or penetrometric method) to determine qnet . The coefficient iδ reflects the taking into account of a possible inclination of the load considered, while the coefficient iβ makes it possible to take into account the effect of a possible slope near the foundation. In the absence of an inclination or slope (or for an embankment located at a distance greater than d = 8 B – cf . Figure 9), we have respectively iδ = 1 or iβ = 1.

Table 18 summarizes the different possible cases and gives the corresponding qnet expressions.

 

2.5.2 - Calculation of coefficient iδ

The calculation value of the inclination of the load with respect to the vertical is as follows:

[Formula D.2 .4 (1)]

 

With:

Hd: calculation value of the horizontal component of efforts;

Vd: calculation value of the vertical component of the efforts.

iδ is the lift reduction coefficient related to the inclination of the load, it is 1.0 if the load is vertical (Hd = 0).

Otherwise, it is calculated according to the nature of the soil under the foundation as described in Table 16. The abacuses of annex B also allows iδ to be determined from the various soil and foundation parameters.

 

Table 16: Evaluation of the lift coefficient iδ related to the inclination of the load according to the rubbing or coherent nature of the ground under the sole

 

The parameters γ' (effective soil density) in the presence of water or γ (soil density) otherwise, Ⴔ' (effective friction angle) and c' (effective cohesion), are determined by averaging the values of the different soils present over depth hr from the base of the sole.

 

The δd angle is always positive (in absolute value), which means that vertical and horizontal loads must always be counted positively.

The angles δd and Ⴔ ' are expressed in radians in the formulas.

 

In general, the value of the reducing coefficient iδ is quite similar for purely rubbing soils and rubbing and coherent soils: the rubbing character of the ground therefore has a greater influence on the phenomenon of reduction of bearing related to the inclination of the load compared to the coherent character. Finally, the following trends are observed in the value of iδ for rubbing and consistent soils:

• the influence of soil density is low; however, if γ' or γ increases, the value of iδ decreases;

• if the internal friction angle of the soil Ⴔ' increases, the value of iδ approaches the value for pure soil rubbing (the influence of cohesion decreases);

• if the value of effective cohesion c' increases, the value of iδ increases for coherent and rubbing soils while remaining closer to the value for purely rubbing soils than to that of purely coherent soils;

• if the value of the equivalent flush-mounting De increases, the value of iδ for rubbing and coherent floors increases.

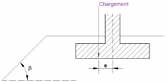
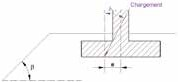
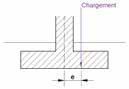
In the case where the effects of eccentricity and inclination are antagonistic(32) (cf. . Table 18) The inclusion of term iδ is too pessimistic. It is necessary to carry out a specific study (possibly with numerical calculation software for example) so as not to over-size the structure.

 

(32) In this case, inclination and eccentricity have a favourable or unfavourable effect respectively on the forces transmitted to the base of the sole.

 

2.5.3 - Calculation of coefficient iβ

 

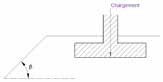
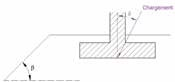
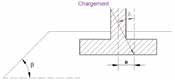
iβ is the lift reduction coefficient related to the proximity of a slope β , it is 1 if the foundation is sufficiently far from the slope (d > 8 B).

d: horizontal distance from the lower corner of the footing to the slope;

β: slope of the slope (Figure 9).

 

Figure 9: Geometric parameters for the calculation of bound iβ the presence of an embankment

 

The coefficient iβ is calculated as described in Table 17 (only for an angle of the inclination lower (33) at 45°). The charts in Annex C also make it possible to determine iβ from the different parameters of soil and foundation.

 

(33) Centrifuge tests to determine the values of the coefficient of reduction of lift due to the presence of a slope were indeed carried out for slope angles of less than 45°.

 

Table 17: Evaluation of the lift coefficient iβ related to the presence of a slope

 

The parameters γ' (effective density of the soil) in the presence of water or γ (density of the soil) otherwise, Ⴔ' (effective angle of friction) and c' (effective cohesion), is determined by calculating the average over the depth hr (i.e. from the base of the sole).

 

The angles β and Ⴔ' are expressed in radians in the formulas.

 

In general, the value of the reducing coefficient iβ is quite similar for purely rubbing soils and rubbing and coherent soils: the rubbing character of the soil therefore has a greater influence on the phenomenon of reduction of lift related to the proximity of an embankment compared to the coherent character. Finally, the following trends are observed on the value of iβ for rubbing and consistent soils:

• the influence of soil density is low; however, if γ' or γ increases, the value of iβ decreases;

• if the internal friction angle of the ground Ⴔ' increases, the value of iβ approaches the value for soils purely rubbing (the influence of cohesion decreases);

• if the value of effective cohesion c' increases, the value of iβ increases for coherent and rubbing soils while remaining closer to the value for purely rubbing soils than to that of purely coherent soils;

• if the value of the equivalent flush-mounting De increases, the value of iβ for rubbing and coherent floors increases.

 

2.5.4 - Cumulation of coefficients iβ and iδ

 

In the case of simultaneous consideration of an inclination of the load and the presence of an embankment, two cases are possible:

 

• the inclination of the load is directed towards the outside of the embankment:

 

• the inclination of the load is directed towards the inside of the slope and the following simplified expression may be used (34):

 

It is recalled that in the case where the effects of eccentricity and inclination are antagonistic, the consideration of iδ is too pessimistic because the influence of inclination quickly becomes negligible compared to that related to eccentricity. A specific study should be carried out to determine the overall reduction coefficient (35) in order to optimise the sizing of the structure. In the case of small works, this study is not essential, we just have to keep in mind that they will not be optimized on this point.

Table 18 summarizes, for each of the possible situations, the formulas of qnet to be used in the case of the method pressiometric (for the penetrometric method, the approach is similar by replacing in the formulas kp by kc and ple* by qce).

 

(34) The effects of slope and inclination are antagonistic. It is then necessary to replace the product iβ x iδ by the coefficient iβδ.

(35) Such specific studies may consist of numerical calculations based on finite element methods, finite differences or similar differences.

 

 

Table 18: Expression of qnet