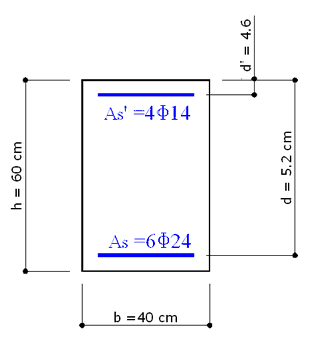
The above cross section of a beam refers to Example 7.3 in /4/. C30/37 is the concrete class and B450C is the steel grade.
The concrete design strength is: fcd = αcc⋅ fck / γc = 0.85 ⋅ 30 / 1.5 = 17.0 Mpa
The steel design yield strength is: fyd = fyk/ γs = 450/1.15 = 391.3 Mpa
The problem is to assess crack width under the following bending moment Mx = 300 kNm (SLS frequent combination) assuming αe = n = Es/Ec = 15.
We want check the same section with the program and compare the results.
INPUT DATA
Once opened a new calculation (by means the command "New" in the menu File) it is important to control if the default Code setting options agree with those in the given example to compare.
In Materials Library we must control if the parameter αe = n = Es/Ec is set to 15 (see column n coeff.) for the concrete class C30/37:

The filled General Data and the pertinent Section Data windows are:


In General Data window the section has been entered as a Predefined typology; as Member Characteristic we selected "beam"; as Options for SLS we selected "n method".
In Section Data window we entered the exact data of the of the aforementioned comparative example.

In the above Forces window we assigned, we selected the SLS Frequent load comb. row and then entered in the grid the values 300 kNm for the moment Mx.
Note that we have to assign, for any section to calculate, at least one Ultimate Load combination (in this example we assigned Mx=450 kNm).
RESULTS
Selecting the Checks tab we obtained the below results window and the printed results window (which command is on the local tab bar) with reference to SLS load combination of our interest. In particular the crack width wk is 0.200 mm different from wk =0.184 in the reference example as the author erroneously evaluates αe= 15 instead of αe=Es/Ecm [see(7.9)EC2].
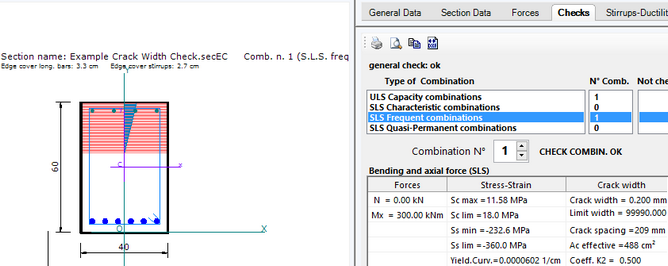

In the above output are printed also the stress and all intermediate values calculated by program (for example the effective tension area of concrete Ac = 487 cm²).
The program perform also the check of minimum reinforcement areas (§ 7.3.2):

If we remake the input of the same section as a general section we can note a slight difference between the crack width wk.(wk =0.201 mm instead of 0.200). This is due to the different way to assess the tension effective concrete area Ac (see Limitation of crack widths topic). The below graph showed by program for SLS combinations make in evidence with blue points the effective tension area calculated as circles the diameter of which is equal to 7 diameters of the corresponding tensile bars (the circles are limited by the rules laid down in §7.3.2(3) EC2).
