Attention: The file of the deflection beam and the corresponding files of its sections must belong to the same directory.
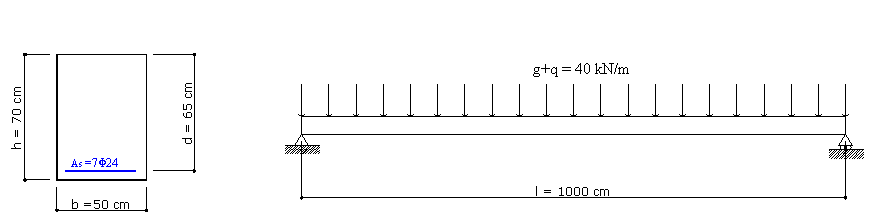
The above beam refers to Example 7.6 in /4/ that concerns the evaluation of the vertical displacement in the mid-span of the beam with the constant transversal section depicted in the same figure. This problem is resolved firstly in a cumulative way stating αe = Es/Ec = n = 15. Shrinkage not considered.
C30/37 is the concrete class and S450C is the steel grade with Ecm = 32837 MPa.
In present program the use of the αe parameter is equivalent to use the following effective creep coefficient [see eq.(7.20) EC2]:
Ec,eff = Ecm/(1+φ(∝,t0) = n / Es
from wich the equivalent creep coefficient φ to use in the program is:
φ = φ(∝,t0) = n Ecm/Es -1 = 15 x 32837,0/200000 -1= 1,463
Before to calculate the beam deflection we have to generate the constant predefined transversal section which file that we named "Transversal_1.secEC". In this section we have select the above materials and set in the C30/37 concrete row of Materials Library: creep coefficient φ = 1.463 , aging coefficient χ=1 (EM method) and shrinkage coefficient = .000000001 i.e. null value:

The input window of the section "Transversal_1.secEC" is:
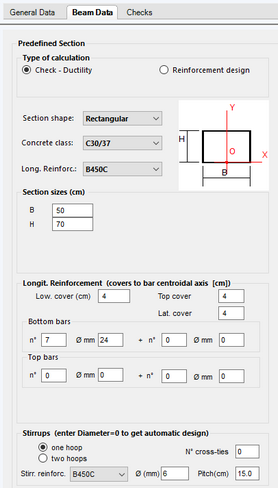
Assigned Stirrups data and Forces of section are not used in the deflection calculation of then beam but their definition have the sole purpose to complete section input and so save its file.
At this point, in a new and separate calculation after selecting the 'Beam Data' Tab, we made the following input of the "Single beam deflections" typology:
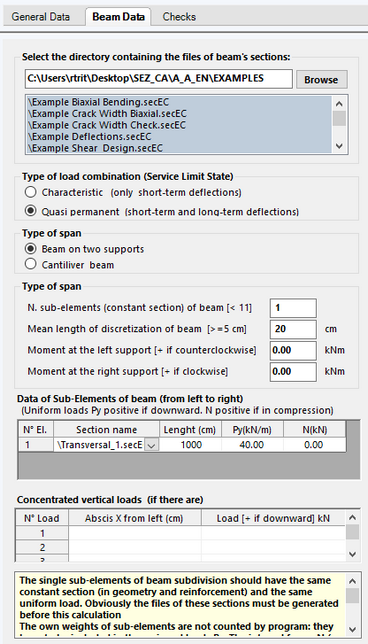
Firstly we selected the directory were saved the transversal section named "Transversal_1.secEC". Then the type of span (Beam on two supports" and the following numerical data:
- N. sub-elements of beam = 1 (in this case we have a constant section over the entire span of the beam)
- Mean length of discretization of the beam = 20 cm
- Moments at the end supports (both zero in this case)
In the Data of sub-Elements of beam (there is only one sub-element) we have to select (in the drop-down list) the name of the above section, the length of the sub-element (in this case coincides with the length of span = 1000 cm), the assigned distributed load Py= 40 kN/m. There is no concentrated load over the span.
Immediate following results are furnished by the program:

In the check window we can see the max positive deflection for short time effects (2.703 cm > 2.164 cm of the original example) and for long time effects (3.657 cm > 3.571 cm of the original example). The slight difference is due to the simplified method performed in in /4/.
Note the warning relating the max stress check calculated with the AAEM method. Maximum value of concrete compressive stress is 13.62 Mpa > 13.50 Mpa critical concrete compressive stress. Performing the stress with n simplified method (αe = 15) max stress results, instead, equal to 12.94 Mpa < 13.50.