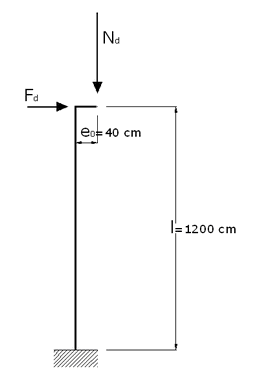
We want to assess the ultimate limit state of instability for the above isolated cantilever column only for X direction as in the example reported in /7/.
In the above Section Data window are assigned (no data for Y direction):
- Concrete class: C40/50
- Steel: B450C
- Dimensions (Side X, Side Y) of the rectangular section of the column: 70x70
- The longitudinal bars 10+10Φ24 are assigned as 1 bar Φ24 /corner and n. 8 web bar Φ24 along Y direction.
- Design constant axial force: 1000 kN
- First order moment MX0d = Nd ⋅ e0 + Fd ⋅ l = 1000 ⋅ 0.40 + 40 ⋅ 12.00 = 880.00 kNm
- Eccentricity eX for geometric imperfections: 0.00 cm (already included in e0)
- Effective length l0X = 1200 ⋅ 2 = 2400 cm according to fig. 5.7 g) in §5.8.3.1
We first check the option "Uniaxial Nominal method" [eq. (5.34)EC2]. The output is:

We note the second order moment 385 kN very near to 390 kN obtained in /7/ with the same method (Resistant moment are also near).
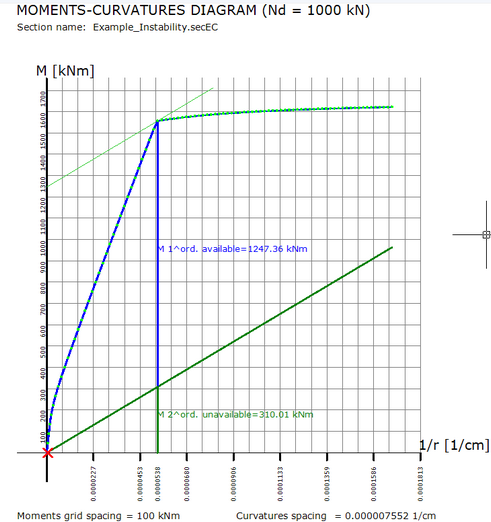
If we check the option "Biaxial Model Column method" (moment-curvature diagram) the output is:

Last results are less conservative but near to the previous. The "model column" diagram is: