Il calcolo delle tensioni in esercizio svolto col metodo semplificato illustrato in precedenza è in genere sufficiente a descrivere lo stato tensionale in esercizio di sezioni in c.a. normale prevalentemente inflesse e fessurate.
In presenza di sforzo normale di compressione come nel caso dei pilastri e, di norma, nel caso di sezioni precompresse, si impone spesso una valutazione più accurata delle tensioni e delle deformazioni lente dovute alla viscosità ed al ritiro.
Le norme italiane non indicano una specifica modalità di calcolo per tale valutazione limitandosi a fornire unicamente i coefficienti di viscosità e ritiro (§11.2.10.7 e §11.2.10.6 NTC).
Tratteremo di seguito il metodo AAEM (Age Adjusted Effective Modulus) che rappresenta lo stato dell’arte nelle applicazioni tecniche.
Nell’ambito delle sezioni in c.a. normale qui trattate, questo metodo appare oggi il più rapido per una attendibile valutazione delle deformazioni viscose e da ritiro, anche nel caso di sezioni fessurate. Nel presente paragrafo verrà esposto il calcolo delle tensioni con il metodo AAEM prescindendo, nel caso di sezioni fessurate, dal tension stiffenig e, quindi, dal connesso calcolo di deformazione. Tale aspetto deformativo, che coinvolge anche la valutazione dell’apertura delle fessure, verrà affrontato nell'ambito del calcolo delle deformazioni.
Il metodo AAEM si basa su di un duplice calcolo della sezione:
| • | calcolo delle tensioni istantanee al tempo iniziale t0 di messa in carico |
| • | calcolo delle variazioni delle tensioni per viscosità e ritiro che intervengono dal tempo t0 al tempo successivo t (in genere a tempo infinito) mediante un’unica valutazione incrementale che utilizza per il conglomerato un particolare modulo elastico lineare corretto da applicare unicamente agli incrementi tensionali e deformativi che si sviluppano successivamente alla messa in carico. |
Nella formulazione del metodo A.A.E.M. che verrà esposta nel seguito, si fa l’ipotesi che le sollecitazioni nella sezione (flessione e sforzo normale) restino costanti nel tempo. Tale ipotesi è a rigore lecita solo per strutture isostatiche, mentre per quelle iperstatiche essa conduce a risultati solo approssimati, a meno di non mettere in conto gli incrementi di sollecitazione prodotti dalle variazioni delle reazioni vincolari dovute agli effetti differiti (tali reazioni iperstatiche possono ottenersi in generale solo mediante un calcolo non lineare ed iterativo, in funzione della deformazione finale visco-elastica dell’intera struttura, a priori incognita).
Si consideri, ad esempio, un’asta in c.a. isostatica che ad un certo istante iniziale t0 sia sottoposta ad una delle combinazioni di esercizio (tipicamente del tipo quasi permanente). Le sollecitazioni N, Mx, My che si sviluppano in ogni sezione in conseguenza della combinazione all’atto dell’applicazione dei carichi determinano un campo di tensioni iniziali σ0 nel calcestruzzo e nell’acciaio. Col passare del tempo, pur rimanendo le sollecitazioni applicate costanti, si assiste ad una progressiva variazione delle tensioni e delle deformazioni nei due materiali prodotta dal ritiro e dalla viscosità del calcestruzzo.
Per poter calcolare tale ridistribuzione delle tensioni in un generico istante t > t0 è preliminarmente necessario stabilire una idonea modellazione del ritiro e della viscosità. Tale modellazione è operata a mezzo dei seguenti parametri reologici:
Funzione ritiro: il ritiro è dovuto principalmente all’essiccamento ed alla carbonatazione del calcestruzzo nella fase di maturazione. Esso produce un graduale accorciamento del materiale, che, in assenza di vincoli ed armature, è definito dalla funzione ritiro espressa di solito sulla base delle età t0 e t poste come riferimenti iniziale e finale in cui si vuole valutare la deformazione unitaria libera:
ecs = ecs(t,t0)
Il ritiro dipende, inoltre, dalla forma della sezione, dall’umidità relativa ambientale e dalle caratteristiche intrinseche del materiale. Le NTC forniscono, tra l'altro, i valori finali del ritiro (a tempo infinito) εcs(t∞,t0) da utilizzarsi in mancanza di sperimentazione diretta.
Viscosità: la viscosità del calcestruzzo viene descritta, in assenza di vincoli ed armature (viscosità intrinseca), a mezzo del coefficiente f(t,t0) definito come rapporto tra la deformazione unitaria al tempo t e la deformazione elastica istantanea in un provino soggetto ad una tensione costante σ0 applicata al tempo t0 :
f(t,t0) = s0 / e0 (1)
con e0 = s0 / Ec(t0) (2)
Ec(t0) = modulo elastico al tempo t0
La teoria elasto-viscosa lineare, impiegata nella presente procedura, è valida per un livello tensionale non superiore al 40÷45% di fck; al di sotto di tale livello il modulo elastico Ec viene considerato ancora costante (indipendente dalla tensione applicata, ma variabile nel tempo).
Il valore di f è maggiore se l’età t0 dell’applicazione della tensione costante s0 è minore, e si incrementa all’aumentare dell’intervallo temporale (t-t0) in cui detta tensione resta costante. Come per il ritiro, la funzione f di viscosità dipende dalla geometria della sezione, dall’umidità e dalla qualità del conglomerato.
Valori finali f(t∞,t0) sono forniti dalle NTC in assenza di sperimentazione diretta (§11.2.10.7). Nell'apposito programma di servizio vengono illustrate formule per il calcolo dei valori di f al tempo t generico, anch’esse implementate nel già citato programma di servizio.
Esplicitando dalla (1) la deformazione al tempo t, ed esprimendo e0 in funzione della tensione applicata (2), si ha:
e(t,t0) = s0 [1 + f(t,t0) ]
Se, a partire dall’istante t0 di applicazione della tensione s0 , si ha una graduale riduzione di tensione ds , il principio di sovrapposizione consente di esprimere la deformazione al tempo t, come segue (comprendendo anche il ritiro):
e(t) = ecs(t,t0) + s0 [ 1 + f(t,t0) ] / Ec(t0) +![]() Ec(t) [1+f(t,τ)] ds (3)
Ec(t) [1+f(t,τ)] ds (3)
Il coefficiente di invecchiamento c
Le notevoli difficoltà connesse all’integrazione dell’equazione integro-differenziale (3) sono evitate sostituendo alla effettiva storia di carico σ(t), un unico incremento di tensione Δσ ed un coefficiente di viscosità f(t,t0) ridotto a mezzo del cosiddetto coefficiente di invecchiamento c = c(t,t0):
e(t) = s0 [1+f] / Ec(t0) + Δs(t) [1+c f] / Ec(t0) + ecs (4)
La (4) consente di algebrizzare l’equazione integro-differenziale (3) sotto la condizione, dimostrata da Z.P. Bazant (1972), che la storia di e(t) sia affine alla funzione (1+f)/Ec, condizione che in pratica si verifica in molti casi.
Il valore di c(t,t0) ha come limiti estremi di variabilità i valori di 0,5 a 1 e può essere calcolato per t e t0 generici. Nella gran parte dei problemi pratici interessa solo il valore finale c(t∞,t0), che per t0 maggiore di 15 giorni può essere assunto sempre pari a 0,8. Il CEB "1990" Model Code ne propone un valore approssimato funzione solo dell'età t0 di messa in carico:

Poichè c è coefficiente moltiplicativo di f , il cui valore esatto è di difficile determinazione, una grande accuratezza nella valutazione di c può essere giustificata solo in rari casi e per opere di importanza non corrente.
Modulo di elasticità corretto
Introducendo nella (4) il modulo elastico cosiddetto “corretto per l’età” del conglomerato definito dalla:
Ec*(t,t0) = Ec(t,t0) / (1+ c.f) (5)
si ha:
e(t) = s0 [1+f] / Ec(t0) + Δs(t) / Ec(t,t0) + ecs(t,t0) (6)
La (6) è alla base del metodo AAEM per il calcolo delle sezioni e delle strutture in c.a. in fase elasto-viscosa lineare. La (6) è suscettibile della rappresentazione grafica sotto rappresentata in cui la tensione rappresentativa della compressione del calcestruzzo subisce un primo incremento O-A per effetto dell’applicazione istantanea delle sollecitazioni cui corrisponde nella (6) la deformazione elastica iniziale e0 = s0 / Ec(t0) contenuta nel primo addendo. Il tratto orizzontale A-B corrisponde all’applicazione delle distorsioni libere per viscosità e ritiro che si sviluppano nell’intero periodo t-t0 , costituite dalla deformazione unitaria per ritiro ecs(t,t0) e da quella viscosa s0 ⋅f(t,t0) / Ec(t0) contenuta pure nel primo addendo della (6). Il tratto B-C corrisponde al secondo addendo della (6) ed equivale ad una seconda soluzione elastica ottenuta con il modulo elastico corretto per l’età Ec*.

Il calcolo delle tensioni col metodo AAEM
Si consideri una generica sezione costituita da uno o più domini di conglomerato anche di differente resistenza, modulo elastico e caratteristiche reologiche, la cui geometria sia rappresentata nella modalità più generale descritta nei precedenti capitoli.
Si è già detto che il metodo AAEM prevede due distinte fasi di calcolo, la prima relativa ai soli effetti istantanei, la seconda ai soli effetti differiti. Sotto l’azione di una delle combinazioni di carico di esercizio la sezione è soggetta, al tempo t0 di messa in carico, alle sollecitazioni N, Mx, My cui corrispondono le deformazioni a0, b0, c0 deducibili dalla risoluzione iterativa del sistema lineare (7), nei cui coefficienti (6) i moduli elastici Ecj sono quelli al tempo t0. Per le barre d’armatura il modulo elastico viene assunto costante per entrambe le fasi di calcolo e pari al valore Es. Calcolate le deformazioni istantanee a0, b0, c0 , sono immediatamente determinabili le tensioni (3) in ogni punto della sezione.
La seconda fase del procedimento consiste nel calcolare le variazioni delle deformazioni Δa0, Δb0, Δc0 che intervengono gradualmente nella sezione dal tempo t0 al tempo finale t per effetto del ritiro e della viscosità in costanza delle sollecitazioni N, Mx, My.
Le coazioni nel generico dominio j di calcestruzzo sono descritte mediante i coef-ficienti fj(t,t0), cj(t,t0), ecs(t,t0), Ec*(t,t0) precedentemente introdotti.
La tecnica di rilassamento impiegata (vedasi al riguardo [5],[6]) consiste anzitutto nel calcolo degli sforzi di incastro perfetto N*, Mx*, My* da applicare alla sezione per impedirne ogni deformazione causata dai fenomeni reologici. Si considerino, a tal fine, i singoli domini (sottosezioni) privi di congruenza reciproca e di ogni aderenza con le barre di armatura. Il generico dominio j presenterebbe, in siffatta ipotesi, al tempo t le seguenti deformazioni di sottosezione:
Δaj = fj(t,t0) ⋅ a0
Δbj = fj(t,t0) ⋅ b0 (7)
Δcj = fj(t,t0) ⋅ c0 + ecs j(t,t0)
Gli sforzi N*, Mx*, My* si ottengono applicando le (6) al solo conglomerato reagente con modulo elastico corretto per l’età Ecj* = Ecj*(t,t0) :
N* = ∑j Ecj* Acj Δcj + ∑j Ecj* Sxcj Δbj + ∑j Ecj* Sycj Δaj
Mx* = ∑j Ecj* Sxcj Δcj + ∑j Ecj* Jxcj Δbj + ∑j Ecj* Jxycj Δaj (8)
My* = ∑j Ecj* Sycj Δcj + ∑j Ecj*Jxycj Δbj + ∑j Ecj* Jycj Δaj
o, in notazione matriciale:
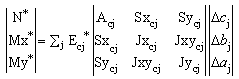
![]() (9)
(9)
Per ripristinare la congruenza nella sezione complessiva, nell’ipotesi di conservazione delle sezioni piane anche durante la fase viscosa, occorre applicare le azioni di incastro perfetto all’intera sezione (cioè ai vari domini di conglomerato più le armature). Ciò si ottiene applicando ancora la (7) del capitolo delle Tensioni Ammissibili in cui si ponga Ecj = Ecj*:
![]()
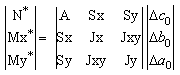 (10)
(10)
Finalmente note le incognite Δa0, Δb0, Δc0, la variazione di tensione nell’intervallo temporale t-t0 si ottiene dalla (4) applicata per il generico punto di coordinate x,y del dominio j:
Δsj = Ecj* Δecj - Ecj* ( fj ⋅e0 + ecs j)
dove:
Δecj = Δa0 ⋅ x + Δb0 ⋅ y + Δc0
e0 = a0 ⋅ x + b0 ⋅ y + c0
La deformazione totale della sezione al tempo t risulta infine:
atot = a0 + Δa0 = χy tot
btot = b0 + Δb0 = χx tot (11)
ctot = c0 + Δc0 = eOrigine
Tali coefficienti definiscono, altresì, la posizione finale dell’asse neutro delle deformazioni di equazione :
atot x +btot y + ctot =0
Le tensioni totali finali nel conglomerato sono (vedi figura):
stot = st = s0 + Δs
Le tensioni finali nella generica barra d’acciaio i di coordinate xi , yi :
si tot = si 0 + Δsi
con:
si0 = Es ( a0 ⋅ xi + b0 ⋅ yi + c0 )
Δsi = Es (Δa0⋅ xi + Δb0⋅ yi + Δc0 )
Parzializzazione della sezione
Le tensioni in esercizio calcolate con il procedimento appena descritto sono ottimamente approssimate nel caso in cui per la data combinazione degli sforzi N, Mx, My, la sezione risulti interamente compressa (è ad esempio il caso della presso-flessione con piccola eccentricità nei pilastri). In questo caso anche le deformazioni (11) possono essere considerate attendibili ai fini della determinazione delle frecce e delle rotazioni dell’elemento strutturale cui la sezione appartiene.
Nel caso in cui in un punto qualsiasi della sezione venga superata la resistenza a trazione per flessione fcfm , verrà considerata reagente la sola parte compressa della sezione di conglomerato che, in zona tesa, pertanto, non potrà assorbire alcuna tensione di trazione. In tale evenienza viene introdotta la seguente ulteriore ipotesi semplificativa (cfr. [7]):
durante l’intera seconda fase viscosa (da t0 a t) si considera reagente la sola parte della sezione compressa al tempo t0 di messa in carico, sebbene, per effetto del ritiro e della viscosità, l’asse neutro delle tensioni tenda a spostarsi. L’errore che così si introduce è in genere piccolo in quanto si trascurano le tensioni di compressione che tendono a svilupparsi nelle adiacenze dell’asse neutro e che proprio per tale vicinanza sono di piccola entità. La semplificazione di calcolo è, invece, notevole se si pensa che per il calcolo dell’incremento tensionale e deformativo non occorre più impiegare un metodo iterativo, in quanto, restando fissata al tempo t0 la sezione resistente di calcolo, diventa lecita la sovrapposizione immediata delle tensioni in ogni punto di tale iniziale sezione reagente.
E’ importante notare che, sempre nel caso di sezioni fessurate, le deformazioni della sezione prima considerate nel calcolo (sia al tempo t0 che al tempo t) non sono utilizzabili per un calcolo di deformazione dell’asta di appartenenza della sezione, essendosi trascurato nel procedimento sin qui esposto (finalizzato al solo calcolo delle tensioni) l’effetto irrigidente (tension stiffening) del conglomerato teso compreso tra due qualunque sezioni fessurate consecutive.
Il calcolo delle deformazioni di una trave in presenza di viscosità, ritiro e fessurazione verrà affrontato nel paragrafo relativo allo stato limite di deformazione sulla base di un metodo proposto da A. Ghali e R. Favre in [7] ma che in pratica è pienamente concordante con le NTC ed EC2 .
Implementazione del metodo AAEM nel programma di calcolo
E’ importante notare che operando col metodo semplificato si ottiene dalla elaborazione un solo risultato in quanto la normativa fissa un unico “modulo efficace” per il conglomerato (Ec = Es / n), mentre col metodo AAEM occorre in ogni caso fissare i moduli elastici e i parametri reologici dei materiali, che variano a seconda delle condizioni ambientali e del tipo di determinazione effettuata. Le tensioni e deformazioni calcolate perdono, di conseguenza, di univocità a causa dell’assenza, in normativa, di parametri meccanici e reologici di tipo convenzionale tali da rendere possibile il confronto delle tensioni e dell’apertura delle fessure.
In altre parole l’enorme variabilità della ridistribuzione delle tensioni in dipendenza dei valori assunti per il coefficiente di viscosità e di ritiro rende aleatorio il confronto con i valori limite delle tensioni e dell’apertura delle fessure fissate nelle NTC.
A differenza del metodo semplificato i valori dei moduli elastici del conglomerato e dell’acciaio che intervengono nel calcolo vengono prelevati direttamente dall’archivio materiali (il modulo elastico del conglomerato Ecm in archivio si riferisce a quello istantaneo all’atto dell’applicazione del carico). Ciò vale anche per il coefficiente di viscosità fj(t,t0), per il coefficiente di invecchiamento c j(t,t0), il ritiro unitario ecs j(t,t0) , la resistenza media a trazione fctm ed i prodotti tra coefficienti b1⋅b2 di tension stiffening.
La verifica delle tensioni viene effettuata a sezione interamente reagente nel caso in cui in nessuna combinazione di esecizio venga superata la massima resistenza a trazione fctm. Nell’eventualità contraria la verifica delle tensioni verrà effettuata senza tenere in alcun conto tale resistenza a trazione.
Il calcolo dell’apertura delle fessure e della deformazione della sezione sono, invece, effettuate tenendo conto della collaborazione del calcestruzzo teso (tension stiffening) così come verrà illustrato nei successivi paragrafi.