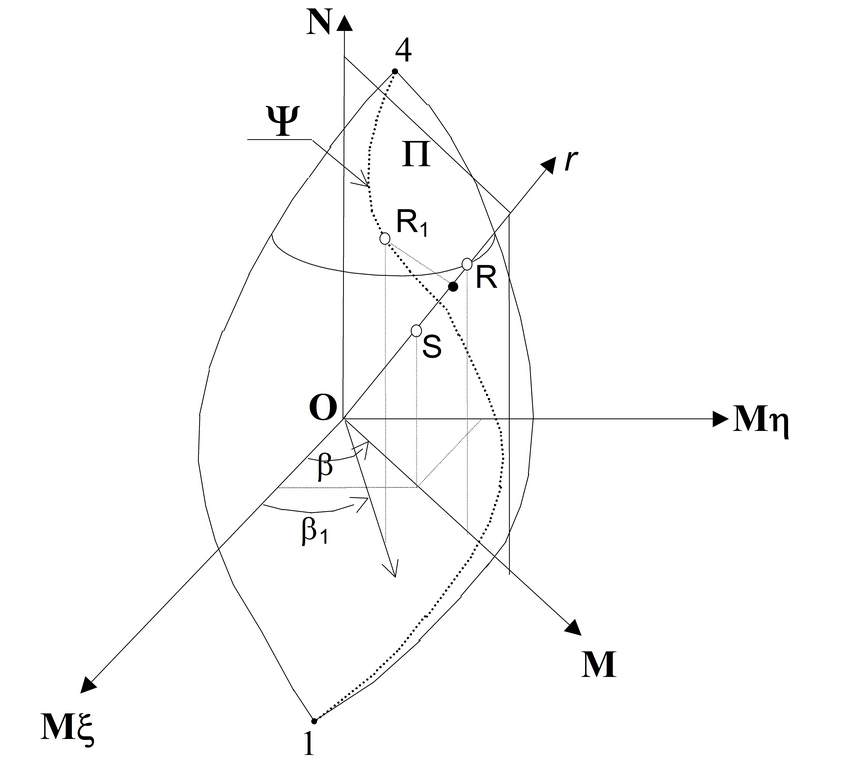
Stati limiti ultimi per tensioni normali > Misura della sicurezza ad eccentricità costante

Questa misura viene operata in perfetta analogia al criterio di misura della sicurezza ad eccentricità costante sviluppato relativamente alle sollecitazioni rette. Definito il punto S come rappresentativo degli sforzi esterni ⎨NSd, MξSd ,MηSd⎬ , la misura della sicurezza è fornita (vedi figura) dal rapporto tra i moduli dei segmenti ed misurati sulla retta r appartenente al piano Π passante per l’asse degli sforzi normali N e caratterizzato dal formare con l’asse Mξ l’angolo costante β:

β = arctan (MηSd / MξSd ) (1)

Il problema di verifica così posto consiste nel ricercare quella particolare direzione α dell’asse neutro la cui corrispondente curva spaziale di interazione Ψ intersechi il piano Π proprio nel punto R di intersezione tra la retta r di misura e la superficie di interazione. Appartenendo il punto R al piano Π, le relative componenti MηRd, MξRd formano, pertanto, lo stesso angolo β espresso dalla (1).

L’ultima considerazione espressa fornisce la chiave del criterio di convergenza adottato. Tenendo fisso, infatti, un valore di tentativo dell’angolo α (direzione asse neutro) si risolve un problema di verifica ad eccentricità costante per presso-flessione retta applicato ad una curva di interazione piana N-M, in cui il singolo momento M di frontiera è costruito a partire dalla proiezione delle componenti MξR , MηR (generico punto della curva tridimensionale Ψ) sul piano Π:

M = MξR ⋅ cos β + MηR ⋅ sin β

Sia R1⎨N1, Mξ1, Mη1⎬ il punto della curva Ψ corrispondente alla soluzione trovata sulla retta di misura nel piano N-M ipotizzato. Tale punto apparterrà al piano Π e, quindi, sarà la soluzione del problema, se e solo se risulterà (entro una prefissata tolleranza):

β1 = arctan (MηR1 / MξR1 ) = β

Ove tale circostanza non sia riscontrata (come ad esempio accade in figura), occorrerà incrementare l’angolo α di una quantità finita Δα e ripetere il procedimento di integrazione delle tensioni ottenendo un nuovo valore β2. Così di seguito fino ad individuare un settore angolare definito da due valori consecutivi di α in corrispondenza dei quali i valori calcolati per βi, βi+1 rispettino la condizione:

βi ≤ β ≤ βi+1 con βi ≤ βi+1

A questo punto la convergenza verso il voluto valore di β è assicurata, entro una prefissata tolleranza angolare, mediante il solito procedimento della bisezione.