In linea generale il calcolo delle tensioni normali in esercizio è alquanto complesso dovendo tenere conto non solo delle combinazioni dei carichi esterni sopra definite, ma anche, se necessario, degli effetti della viscosità, del ritiro, delle variazioni termiche e delle deformazioni impresse di altra origine (cedimenti vincolari, etc.).
Sulla base delle azioni di progetto rare e quasi permanenti SLE vanno calcolate le tensioni massime nel calcestruzzo e nell'acciaio che devono essere inferiori ai limiti imposti dalle NTC nel § 4.1.2.2.5 (0.6 fck per la combinazione caratteristica, 0.45 fck per comb. quasi permanenti e 0.80 fyk per l'acciaio).
Le Istruzioni NTC nel § C4.1.2.2.5 indicano che qualora si ritenga possibile effettuare un'unica verifica indipendente dal tempo il calcolo può essere effettuato con il metodo n in cui il coeff. di omogeneizzazione n può essere assunto pari a 15.
In ogni caso il calcolo delle tensioni viene svolto nel presupposto di comportamento elastico e di perfetta aderenza di tutti i materiali, nonchè di assenza di resistenza a trazione del calcestruzzo nel caso di trazione.
Trattando qui di sezioni rinforzate è necessario calcolare le tensioni in due fasi:
1) Calcolo delle tensioni normali di esercizio presenti all'atto del rinforzo. Vanno anzitutto stimati i carichi (pesi propri ed accidentali) effettivamente presenti prima dell'applicazione dei rinforzi e quindi valutate le corrispondenti sollecitazioni N0, Mx0, My0 nella sezione da verificare (da inserire nella scheda di input degli sforzi pre-rinforzo). Il calcolo in questa fase viene svolto in automatico dal programma (che memorizza anche le corrispondenti deformazioni) con il coeff. di omogeneizzazione n=15 in quanto può assimilarsi ad una combinazione quasi permanente (di lunga durata).
2) Calcolo delle tensioni normali sulla base delle sollecitazioni finali assegnate (comprendenti le sollecitazioni precedenti il rinforzo). Questo calcolo viene svolto per sovrapposizione degli effetti trascurando la non linearità causata dalla mancanza di resistenza a trazione del calcestruzzo. In questa fase gli sforzi di calcolo sono quindi costituiti dalla differenza tra gli sforzi finali assegnati N, Mx, My e quelli N0, Mx0, My0 pre-rinforzo. Poichè in genere nelle sezioni iniziali (pre-rinforzo) si sono quasi del tutto esauriti gli effetti differiti (ritiro e viscosità) non appare corretto utilizzare per questa seconda fase di calcolo il coeff. forfettizzato n = 15. Si è preferito quindi utilizzare il metodo EM (Effective Modulus) che consiste nel considerare per ciascun calcestruzzo impiegato un modulo elastico equivalente che tenga conto della viscosità che il calcestruzzo deve ancora sviluppare nell'intervallo di tempo che va dal momento del rinforzo al momento in cui si pensano attive le sollecitazioni assegnate. Si trascura il ritiro in quanto nel caso di calcestruzzo nuovo di rinforzo (ad es. per camicia o solette aggiunte) si utilizzano sempre additivi antiritiro che riducono di molto l'effetto di questa coazione.
Il Modulo elastico equivalente è dato da:
Ec,eff = Ec/(1+f)
in cui Ec è il modulo medio di elasticità normale e f è il coefficiente di viscosità assegnato anch'esso nell'archivio materiali per ognuno dei calcestruzzi inseriti. Volendo assegnare ad esempio un coefficiente di viscosità f equivalente ad un coeff. di omogeneizzazione n basterà porre:
Ec,eff = Ec/(1+f) = Es/n
da cui: f = Ec/Es · n - 1
Per fissare le idee supponiamo di voler calcolare le tensioni a lungo termine (in combinazione quasi permanente) nel caso in cui ad una trave esistente si aggiunga una soletta in ca in zona compressa; al calcestruzzo esistente i cui fenomeni lenti si possono considerare esauriti va assegnato f=0 (nell'archivio materiali), mentre al calcestruzzo nuovo della soletta va assegnato (sempre nell'archivio materiali) il valore di f che si ritiene più opportuno (ad esempio quello corrispondente a n=15). In questo modo nel calcolo di seconda fase i moduli elastici dei due calcestruzzi assumeranno valori più vicini al reale comportamento.
Nel caso si voglia, invece, valutare le tensioni istantanee per effetto di un carico variabile raro (combinazione rara) è necessario modificare il valore di f del nuovo calcestruzzo nell'archivio materiali ponendolo ad esempio nullo o molto piccolo. Da qui la necessità di effettuare differenti calcoli della stessa sezione: uno per ogni tipologia di combinazione SLE di esercizio (dovendo di volta in volta variare il coeff. f).
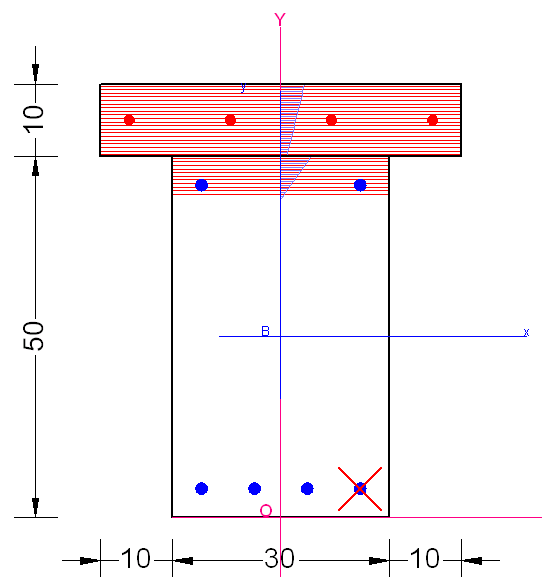
La sezione in figura è stata calcolata assegnando alla soletta di calcestruzzo Classe 20/25 un coefficiente di viscosità f = 1.36 (equivalente ad n=15 per Ec= 31475 N/mm² e Es=200000), mentre per il calcestruzzo della sezione rettangolare esistente si è posto f=0. Il calcolo effettuato in due fasi spiega la circostanza per cui la massima tensione nella vecchia sezione rettangolare (sollecitata da sola nella prima fase pre-rinforzo) risulta maggiore di quella nella soletta.
|
© 2022 Geostru Software