E’ necessario limitare l’entità delle frecce nei solai e nelle travi in c.a. quando possono compromettere:
•la funzionalità delle strutture (al fine, ad esempio, di evitare il ristagno delle acque meteoriche sugli impalcati di copertura, impedire un’eccessiva curvatura alle vie di corsa di carri ponte e simili, etc.);
•il danneggiamento delle pareti divisorie (per stacco e fessurazione dei tompagni in forati; rottura delle vetrate e degli infissi etc.);
•l’estetica delle strutture.
Per la valutazione della deformabilità e dei relativi limiti le NTC (§4.1.2.2.2) rimandano a documentazione tecnica di comprovata validità. Nel seguito si farà pertanto riferimento alla Circolare del 2019 [2].
Si premette che in generale va effettuata la verifica delle deformazioni istantanee in presenza delle combinazioni rare, mentre le deformazioni a lungo termine (t=∞) devono essere verificate per combinazioni di carico quasi permanenti.
Per travi e solai con luci non superiori a 10 metri, la Circolare [2] consente l’omissione delle suddette verifiche dello stato limite di deformazione a condizione che i rapporti di snellezza l/h (l=luce; h =altezza totale sezione) risultino inferiori o uguali ai valori forniti dalla (C4.1.13) del §C4.1.2.2.2. A differenza del DM96 nessuna distinzione viene operata tra travi e solai. Si lascia al lettore l'eventuale applicazione della (C4.1.13).
Il programma calcola, invece, la deformazione flessionale di solai e travi mediante integrazione delle curvature tenendo conto della viscosità del calcestruzzo e del ritiro, così come previsto dalla Circolare 2019.
Dall’esame delle prescrizioni normative risulta evidente che nella progettazione di strutture correnti in c.a. normale il calcolo dello stato limite di deformazione potrà essere evitato progettando le sezioni delle aste in modo che i rapporti di snellezza siano ovunque inferiori a quelli limiti suddetti.
Se si opera invece sulla base del calcolo delle inflessioni il valore limite della freccia in esercizio sarà in genere stabilito, in accordo con il committente, in funzione delle specifiche esigenze di funzionalità dell’opera; nella maggior parte dei casi correnti per evitare il danneggiamento a tramezzi ed infissi a contatto con la trave considerata basterà fissare tale limite ad 1/500 della luce (cfr. [2]) sotto la combinazione quasi permanente (1/250 in assenza di tramezzi ed altri elementi a contatto). Sempre la circolare consente, nel caso di limitazione a 1/500 della luce, di depurare la freccia totale della sua quota parte presente prima della esecuzione delle pareti; operando col presente programma è necessario dapprima calcolare la freccia a lungo termine in presenza di tutti i carichi: se questa supera 1/500 della luce si può effettuare un secondo calcolo caricando la trave (o il solaio) con i carichi presenti prima dell'esecuzione delle pareti e valutare le sole frecce istantanne da sottrarre a quelle totali a lungo termine calcolate in prima istanza.
Deformazione in esercizio di una sezione (metodo AAEM)
Nel caso di sezione non fessurata le deformazioni sono quelle definite nell’ambito del calcolo delle tensioni esposto nei precedenti paragrafi con riferimento al metodo AAEM.Di seguito verrà invece esposto, utilizzando il solo metodo AAEM, il calcolo dei tre parametri di deformazione della sezione (costituiti dai 2 valori di curvatura riferiti agli assi di riferimento assunti e dalla deformazione unitaria nell’origine del sistema di riferimento) nel caso generale di sezione presso o tenso-inflessa fessurata, a partire dalla consueta ipotesi di conservazione delle sezioni piane.
Non si farà cenno, nella presente esposizione, ai metodi semplificati (metodo bilineare, dei coefficienti globali) spesso considerati in letteratura (cfr. [5],[7],8],[9]), in quanto l’uso del calcolatore in applicazione di procedimenti più precisi come l’AAEM ne vanificano di fatto ogni utilità.
In parallelo al calcolo tensionale sviluppato nel paragrafo relativo al calcolo tensionale col metodo AAEM, anche per le deformazioni vengono distinte 2 fasi:
•la prima istantanea per effetto della prima applicazione, al tempo t0, degli sforzi assegnati N, Mx, My;
•la seconda riferita al tempo t > t0 , che tiene conto della graduale applicazione della viscosità e del ritiro in costanza dell’applicazione dei suddetti sforzi.
Calcolo deformazioni istantanee in sezione fessurata
Nell’ipotesi di conservazione delle sezioni piane e di comportamento lineare dei materiali, una sezione si definisce nello stato 1 se, sottoposta alle sollecitazioni N, Mx, My e considerata interamente reagente, in nessun punto la tensione di trazione supera il valore fctm della resistenza a trazione del calcestruzzo. La sezione si definisce invece nello stato 2 allorché, prescindendo totalmente dalla resistenza a trazione del calcestruzzo, la sezione si fessura sotto gli sforzi di calcolo.
In un tronco di trave le sezioni non fessurate comprese tra le sezioni fessurate consecutive, si trovano nel suddetto stato 1 a differenza di quelle fessurate contigue che si trovano (a parità di sollecitazione) nello stato 2. Se si calcolano sia le deformazioni a1, b1, c1 della sezione non fessurata nello stato 1, sia quelle a2, b2, c2 della sezione totalmente fessurata nello stato 2, si definisce la seguente deformazione media della sezione:
cy m = am (t0) = ( 1 - z ) ⋅ a1 + z ⋅ a2
cx m = bm (t0) = ( 1 - z) ⋅ b1 + z ⋅ b2
εO m = cm (t0) = ( 1 - z ) ⋅ c1 + z⋅ c2
in cui il coefficiente di interpolazione z, sulla base di considerazioni sperimentali, è espresso mediante la formulazione di tipo iperbolico:
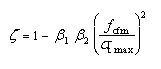
in cui, a favore di sicurezza, si pone fcfm = fctm.
Si noti che qui non compare la limitazione ³ 0,4 che compare nel calcolo dell’ampiezza delle fessure.
Le deformazioni medie così calcolate, possono differire da quelle reali fino ad un ± 30%, ciò a causa della dispersione delle caratteristiche meccaniche e reologiche del calcestruzzo, delle condizioni ambientali e di carico.
Calcolo deformazioni differite in sezione fessurata
Facendo riferimento alla esaustiva esposizione svolta in [7], va dapprima calcolato l’incremento delle deformazioni Δa1, Δb1, Δc1 nello stato 1 per viscosità e ritiro con il procedimento AEEM. La deformazione totale al tempo t risulta pertanto (a sezione interamente reagente):
cy 3 = a3 = a1 + Δa1
cx 3 = b3 = b1 + Δb1
εO 3 = c3 = c1 + Δc1
in cui a1, b1, c1, sono le deformazioni istantanee al tempo t0 nello stato 1.
Nello stato 2 siano Δa2, Δb2, Δc2 gli incrementi delle deformazioni. Le deformazioni totali al tempo t valgono, pertanto:
cy 4 = a4 = a2 + Δa2
cx 4 = b4 = b2 + Δb2 (7.28)
εO 4 = c4 = c2 + Δc2
Interpolando con lo stesso coefficiente ζ tra le deformazioni nello stato 1 e quelle nello stato 2 si ottengono le deformazioni medie della sezione al tempo t:
cy m = am (t) = ( 1 - ζ ) a3 + z a4
cx m = bm (t) = ( 1 - ζ ) b3 + z b4 (7.29)
εO m = cm (t) = ( 1 - ζ ) c3 + z c4
Valutazione delle frecce in travi in c.a. isolate
Sebbene il calcolo delle deformazioni nelle strutture composte da elementi lineari in c.a. esuli dall’ambito delle presenti procedure (rivolte essenzialmente allo studio degli stati limite con riferimento alle sole sezioni), si ritiene opportuno fornire uno strumento di immediata utilizzazione pratica sia pure limitandone lo studio ai due semplici casi di trave isostatica appoggiata agli estremi e di trave incastrata ad un solo estremo (mensola).
Nel caso di travi isostatiche la distribuzione lungo l’asse della sollecitazione normale e flettente resta invariata, nonostante che i fenomeni della fessurazione, viscosità e ritiro modifichino, istantaneamente e nel tempo, rigidezze, curvature e tensioni di tutte le sezioni costituenti la trave.
Nel caso, invece, di travi continue o telai, le azioni iperstatiche applicate alle estremità delle singole travi oltre a differire, all’atto della messa in carico, da quelle ottenute con calcolo elastico per effetto della fessurazione, variano nel tempo a causa delle coazioni viscose e da ritiro che gradualmente si sviluppano nell’intero complesso strutturale.
Trascurando la suddetta ridistribuzione dei momenti, ed applicando (senza variarne l’intensità) alle estremità della trave iperstatica in studio le azioni iperstatiche calcolate elasticamente, è ancora possibile una valutazione sufficientemente accurata delle frecce utilizzando lo stesso procedimento di calcolo sviluppato nel corrente paragrafo per le travi isostatiche ad una campata.
A quest’ultimo proposito si fa presente che un’apposita indagine comparativa sviluppata in [8] mostra come, nel caso di una molteplicità di schemi di travi continue, il calcolo non lineare dei momenti iperstatici di estremità delle singole travi conduca a valori delle frecce in eccellente accordo con quelli ottenuti sulla base dei momenti iperstatici valutati con semplice calcolo lineare elastico.
Le precedenti considerazioni fanno concludere che l’uso del programma per il calcolo delle frecce in travi isostatiche, possa essere esteso con buona approssimazione anche al calcolo delle frecce di travi (e/o solai) iperstatiche di cui siano noti i momenti iperstatici di continuità. Ciò è a maggior ragione plausibile se si tiene conto, inoltre, che la maggiore precisione di un calcolo non lineare delle iperstatiche è comunque viziato dall’aleatorietà connessa alla scelta della resistenza a trazione e degli altri parametri reologici e meccanici del calcestruzzo.
E’ sempre opportuno effettuare (come il programma fa) contemporaneamente al calcolo delle frecce la verifica per tensioni normali ed apertura delle fessure di tutte le sezioni della trave.
La trave appoggiata agli estremi
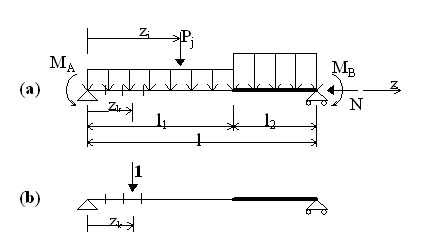
Lo schema di calcolo illustrato in figura (a) prevede la possibilità di assegnare più tronchi (in figura i tronchi di lunghezza l1 ed l2 ) aventi differenti sezioni, armature e carico distribuito. Sempre in figura (a) sono evidenziate, altresì, le coppie MA, MB applicate agli estremi che possono rappresentare le azioni iperstatiche trasmesse dalle strutture contigue. E’ infine prevista un’azione assiale N costante per ognuno dei tronchi in cui è suddivisa la trave, con linea d’azione assunta, per semplicità, passante per il baricentro geometrico di tutte le sezioni. La notevole rigidezza nel proprio piano dei correnti impalcati degli edifici in c.a. consente in genere di porre N=0 per tutte le travi. Ma lo schema può essere utilizzato anche per il calcolo delle frecce e degli accorciamenti assiali di pilastri per effetto dei carichi di esercizio.
Premesso di considerare solo le inflessioni che avvengono nel piano di sollecitazione, e, quindi solo le sollecitazioni rette nelle sezioni, si indica con χ(z) la distribuzione delle curvature prodotte dai carichi concentrati e distribuiti di figura (a) e con M’(z) l’andamento del momento flettente causato dal carico unitario agente sulla struttura di servizio rappresentata nella figura (b). L’applicazione del Principio dei Lavori Virtuali porge per la freccia h in corrispondenza della generica ascissa z di applicazione del carico unitario:
![]()
La distribuzione delle curvature c(z) (corrispondenti ai momenti M(z) dei carichi applicati) non è in generale esprimibile a mezzo di una funzione a causa della non linearità del suo calcolo. L'integrale va pertanto risolto mediante integrazione numerica. A tale scopo il procedimento impiegato nel programma si basa sulla discretizzazione dell’asse della trave in un numero n di conci, ognuno avente lunghezza Δzk e ascissa del suo punto medio, riferita all’appoggio di sinistra, pari a zk. A tutte le sezioni appartenenti ad un singolo concio vengono attribuiti gli stessi valori del momento e della curvatura calcolati nella sezione posta nel punto medio del concio. Di conseguenza, con riferimento al generico concio k di ascissa media zk, l’integrale viene sostituito dalla seguente sommatoria:
![]()
Ponendo nella sommatoria dapprima i valori istantanei delle curvature c nelle sezioni medie degli n conci all’atto della messa in carico e, successivamente, i valori differiti delle curvature per effetto delle successive coazioni, si ottengono due valori di η, rispettivamente al tempo t0 e t , per ognuna delle sezioni zk.
Naturalmente i valori delle singole curvature si riferiscono agli sforzi flettente e normale agenti nella sezione media del concio e supposti costanti per l’intera lunghezza del concio medesimo.
Nel suddetto duplice calcolo delle curvature le sollecitazioni sono considerate solo di tipo retto (M=Mx). La sezione viene calcolata come interamente reagente (non fessurata) se in nessun punto il calcestruzzo supera la resistenza per trazione fctm. Superata tale resistenza la sezione viene considerata fessurata con il calcestruzzo a trazione collaborante alla deformazione media. Non si documentano le semplici formule di equilibrio che consentono il calcolo dei momenti flettenti, nelle sezioni medie dei conci, prodotti dai carichi reali e da quelli unitari virtuali.
Nel caso di sforzo normale N diverso da 0 e di sezioni costituenti la trave caratterizzate da differente geometria, i rispettivi baricentri vengono considerati tutti allineati sull’asse rettilineo della trave, lungo cui agisce lo sforzo normale N.
La trave a mensola
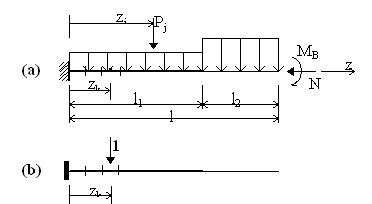
Il calcolo descritto nel precedente paragrafo relativamente alla trave su due appoggi, può essere esteso a qualsiasi struttura isostatica. Si è voluto qui limitare l’attenzione alla mensola solo per via della particolare sensibilità di tale tipologia alle deformazioni flessionali.
La discretizzazione da operare sulla mensola è identica a quella descritta per la trave su due appoggi. Le frecce vanno pure calcolate con le stesse relazioni sopra illustrate in cui, però, le curvature c(zi) ed i momenti virtuali M’(zi) sono valutati in riferimento, rispettivamente, agli schemi grafici relativi alla mensola.