Per le sezioni predefinite il programma esegue il calcolo dell'ampiezza delle fessure sia con il procedimento del DM96, sia con il procedimento alternativo descritto nella Circolare 2018 che riprende integralmente il § 7.3.4 dell'EC2 2005. La scelta opzionale tra i due metodi è prevista nella scheda dei dati generali.
Sempre nella scheda dei dati generali è inoltre possibile (tramite le apposite caselle di scelta) predisporre il calcolo tenendo conto o prescindendo dalla resistenza a trazione del calcestruzzo e facendo riferimento all'intera sezione o alla sola area efficace tesa del calcestruzzo (come più avanti illustrato).
Di seguito si espongono, con riferimento al primo metodo, i principali passi seguiti dal programma durante il calcolo.
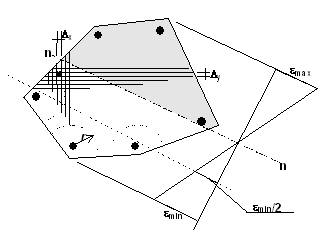
•Calcolo dell’area efficace Ac eff , cioè dell’area di calcestruzzo in zona tesa entro cui le singole barre hanno la capacità di influenzare l’apertura delle fessure. Per le sezioni predefinite, nella versione DM96, in sollecitazione retta lo spessore di quest'area è pari a c + 7,5 Φ in cui c è il copriferro netto delle barre tese di diametro medio Φ; detto spessore deve comunque essere inferiore a (h-x)/2 essendo h l'altezza totale della sezione ed x l'altezza della zona compressa (in assenza di zona compressa si assume h/2). Nel caso di sezioni generiche in presso-tenso flessione deviata, in accordo con la Circolare [4], si ritiene che per la singola barra l’area efficace abbia forma circolare con raggio r pari a 7 volte il diametro della barra. Per il calcolo di Ac eff si fa sempre riferimento all’analisi della sezione nello stato 2 (sezione interamente fessurata). Per ognuno dei domini di calcestruzzo si effettua una discretizzazione (v. figura) in areole di forma pressoché quadrata e lati (Δx , Δy) sufficientemente piccoli in relazione alle dimensioni della sezione (in programma entrambi i lati sono posti pari alla mesh di discretizzazione della sezione settabile nelle opzioni). Passando in rassegna tutte le areole, vengono sommate (a costituire l’area efficace Aceff) solo quelle col proprio baricentro ricadente in una delle aree d’influenza circolari delle barre ed escludendo, prudenzialmente, le areole molto vicine all’asse neutro (nel programma sono escluse quelle con deformazione ε ≥ εmin/2). Solo l’area delle barre tese con ε < εmin/2, vengono quindi sommate a costituire l’area di acciaio, denominata in seguito As, compresa nell'area efficace del calcestruzzo. Nel caso si sia scelto il procedimento secondo l'EC2 lo spessore dell'area efficace del calcestruzzo teso per le sezioni predefinite vale invece 2,5 (h-d) essendo d l'altezza utile della sezione; detto spessore non può superare sia (h-x)/3 che h/2. L'EC2 non prevede esplicitamente (con riferimento a sezioni generiche in presso flessione deviata) un raggio di efficacia del calcestruzzo teso intorno alla singola barra; si è pertanto assunto come raggio il valore di 1,5 cf cioè 1,5 volte la misura del copriferro valutata dal baricentro delle barre preimetrali e comunque di entità non superiore a 7 volte il diametro della barra.
•Calcolo della distanza media srm fra le fessure (metodo DM96), riferita al baricentro delle barre al lembo teso della sezione predefinita. Nel caso di sezioni in presso-tensoflessione deviata (come quella in figura) si assume srm con riferimento alla sola barra più tesa (a favore di sicurezza). Si utilizza la seguente relazione sperimentale (v. Istruzioni [4]):
srm = 2 (c + s / 10 ) + K2 K3 Φ / ρr
in cui:
c = ricoprimento dell’armatura (copriferro netto delle barre longitudinali)
Φ = diametro medio delle barre comprese nell’area efficace come sopra individuata
s = dist. min. tra la barra più tesa e le altre (s ≤14 Φ)
K2 = 0,4 per barre ad aderenza migliorata / 0,8 per barre lisce (opzione da settare nella finestra delle Opzioni armature)
K3 = 0,125 (con flessione semplice o pressoflessione)
= 0,250 (con trazione pura)
= 0,25 [(σ1+σ2)/2σ1] per trazione eccentrica (cioè se tutta la sezione è tesa) o nel caso in cui si consideri solo una parte della sezione; le tensioni limite
s1,s2 sono ricavate nello stato 1 (sezione omogenea non fessurata). Cioè è possibile utilizzare quest'ultima formula anche in flessione semplice o
pressoflessione assumendo come tensione di trazione σ2 (minore in valore assoluto) quella in corrispondenza della fibra estrema dell'area efficace.
E' possibile scegliere tra le due opzioni, solo nel caso di sezioni predefinite, mediante l'apposita casella di scelta nella scheda dei dati generali della sezione.
ρr = As / Ac eff = aliquota delle barre tese ricadenti nell'area efficace sopra definita.
•Calcolo della deformazione unitaria media εsm (metodo DM96) in corrispondenza all'altezza delle barre tese (o della barra più tesa nel caso di sollecitazione biassiale), tenendo conto dell’effetto irrigidente del calcestruzzo teso (tension stiffening), mediante la seguente relazione: εsm = ζ ⋅ σs / Es
| dove : |
| σs = Es εs2 = trazione nella barra più tesa nello stato 2 (fessurato) |
![]()
I simboli rappresentati nella formula precedente hanno il seguente significato:
fcfm = resistenza media a trazione per flessione del cls. Nel programma viene assunta uguale a fctm (prudenzialmente)
σt max = massima tensione di trazione calcolata nel cls. nell’ipotesi di sezione non parzializzata
b1 = coeff. che tiene conto dell’aderenza acciaio-calcestruzzo e vale:
1,0 per barre ad aderenza migliorata
0,5 per barre lisce
b2 = coeff. che tiene conto del fluage di aderenza e vale:
1,0 per carichi di breve durata (istantanei)
0,5 per carichi di lunga durata o ripetuti
Il programma utilizza direttamente i prodotti b1b2 assegnati tra i dati dell'acciaio nell'archivio materiali rispettivamente per sollecitazioni iniziali (prima applicazione dei carichi) e sollecitazioni finali. Per il calcolo dell'apertura delle fessure (metodo n) il programma assume automaticamente il secondo valore per le combinazioni frequenti e quasi permanenti essendo queste le combinazioni per le quali è prescritto questo calcolo (§4.1.2.2.4.1 NTC). Se si utilizza il metodo AAEM il programma utilizza entrambi i valori suddetti. (apertura fessure iniziale all'atto dell'applicazione dei carichi e finale a fenomeni lenti esauriti).
Un discorso a sé merita il coefficiente di interpolazione x che rappresenta l’influenza del calcestruzzo teso compreso tra le fessure (tension stiffening) alla deformazione dell’acciaio. Considerando un tronco unitario di trave sottoposto ad un momento flettente di calcolo M di entità maggiore di quello Msr che produce la prima fessurazione della sezione, si può scrivere la deformazione media dell’acciaio in zona fessurata (analogamente a qualsiasi altra grandezza di deformazione come ad esempio la curvatura [vedi al riguardo la relazione C4.1.11 del §C.4.1.2.2.2 della Circolare 2009]):
εsm = (1 - ζ) εs1 +ζεs2 (2)
in cui εs1 è la deformazione unitaria in sezione interamente reagente (stato 1), εs2 è quella a sezione interamente fessurata (stato 2), ζ è il coefficiente di interpolazione che esprime la frazione di deformazione attribuibile alle sole sezioni fessurate nel tratto di lunghezza unitaria considerato.
Il valore di ζ è dedotto dall’evidenza sperimentale viene valutato dal programma mediante la:
ζ = 1- c (Mf /M)2 (C4.1.12)
in cui c corrisponde in pratica al prodotto b1b2. Il rapporto tra il momento Mf di fessurazione e quello di calcolo M in realtà è uguale al rapporto tra le corrispondenti tensioni indicato nella (1) in quanto nella sezione inflessa non parzializzata l’asse neutro non varia con il momento flettente e, quindi, il rapporto tra le tensioni dell’acciaio che compare nella (1) è uguale al rapporto dei corrispondenti momenti flettenti (stante la linearità del comportamento elastico del calcestruzzo e dell’acciaio ipotizzata nell’ambito degli stati limite di esercizio). Inoltre la (1) vale anche nel caso di trazione pura senza bisogno di sostituire il rapporto Mf /M con Nf /N come invece necessario con la C4.1.12.
Nel caso di contemporanea presenza di momento flettente ed azione assiale nella sezione, si può facilmente estendere lo stesso ragionamento se si ipotizza, per semplicità e senza grosso errore, che l’asse neutro della sezione fessurata non si sposti passando dal momento di prima fessurazione a quello di calcolo. Ciò che a rigore vale solo se l’eccentricità M/N resta costante al variare di M.
Nel caso di calcolo svolto secondo il § 7.3.4 dell'EC2 viene applicata la relazione (7.8) per il calcolo della deformazione media e la (7.11) per il calcolo della distanza massima tra le fessure. Nel caso di trazione eccentrica o per il calcolo riferito solo a parte di sezione il coeffciente K2 = (ε1 + ε2)/ ε1 fa riferimento alle deformazioni di trazione estreme della sezione fessurata (a differenza del DM96 che fa riferimento alla sezione omogenea non fessurata). Viene inoltre semplificata la dipendenza dall'aderenza delle barre mediante un unico fattore kt che tiene conto in maniera forfettaria della durata del carico.