Come descritto nella verifica delle sezioni predefinite le NTC, forniscono la valutazione della resistenza ultima a taglio riferita unicamente a sezioni rettangolari per azioni taglianti parallele all’asse principale d’inerzia ortogonale all’asse neutro (flessione retta o pressoflessione retta). Lo stesso può dirsi con riferimento all’Eurocodice 2 Parte 1 che tratta l’argomento nel § 6.2 con grafici illustrativi riferiti esclusivamente ad elementi resistenti orizzontali (travi) in regime di flessione retta.
Nelle correnti applicazioni progettuali, invece, la verifica dei pilastri in c.a. deve sempre essere condotta in regime di pressoflessione deviata in presenza di entrambe le componenti del taglio riferite, in generale, agli assi principali d’inerzia della sezione di solo calcestruzzo. A seguito, inoltre, dell’introduzione nelle NTC del principio della gerarchia delle resistenze la capacità di resistenza al taglio richiesta ai pilastri è aumentata enormemente al punto da diventare in alcuni casi critica per il dimensionamento (si pensi ad elementi verticali tozzi come nel caso di pilastri nei vani scala interrotti da travi rampanti o di interpiano, o alle pile di piccola altezza per viadotti metropolitani).
Mentre per la pressoflessione deviata sia le NTC che gli Eurocodici forniscono ben due tipi di soluzioni approssimate, nel caso del taglio biassiale non viene data alcuna indicazione, semplificata o rigorosa che sia, in merito alle possibili modalità di calcolo. Analoga situazione si riscontra in tutti i testi di tecnica delle costruzioni e negli articoli divulgativi inerenti le nuove norme. Si propone pertanto il seguente procedimento.
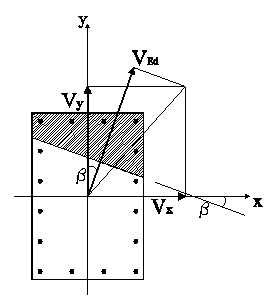
Supponendo noto l’asse neutro allo stato limite ultimo, la risultante dello sforzo di taglio non risulta in generale ortogonale a tale asse (“taglio obliquo”). Anche per la semplice sezione rettangolare di figura risulta evidente che il calcolo della resistenza a taglio condotta separatamente per le due componenti Vx e Vy sulle corrispondenti sezioni rettangolari a lati invertiti, oltre a condurre a risultati a sfavore di sicurezza è concettualmente scorretta in quanto ammette il disaccoppiamento delle componenti Vx, Vy del taglio in realtà non presente allo stesso modo di quello delle componenti Mx, My del momento flettente. Appare pertanto più appropriato assumere come giacitura del traliccio resistente a taglio quella del piano ortogonale alla direzione dell’asse neutro della sezione ottenuta dal calcolo a pressoflessione deviata allo SLU. Di conseguenza il valore del taglio sollecitante il suddetto traliccio sarà costituito dalla risultante VEd della somma delle proiezioni delle componenti Vx, Vy sulla direzione ortogonale a quella dell’asse neutro. Indicato con b l’angolo formato dall’asse neutro con l’asse principale d’inerzia x, il valore di calcolo del taglio risulta:
VEd = Vx sin b + Vy cos b
Si è in tal modo ricondotto il problema del taglio obliquo a quello del taglio in flessione retta. Le sezioni convesse di seguito rappresentate sono state orientate in modo da evidenziare l’ortogonalità tra la direzione del taglio VEd di progetto e l’asse neutro già noto dal calcolo allo SLU per tensioni normali (qui supposto come già effettuato).
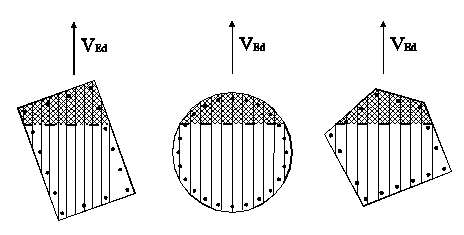
Un approccio razionale al problema della determinazione della resistenza ultima a taglio è quello di suddividere le sezioni in un sufficiente numero di conci elementari (come in figura) tracciati parallelamente alla direzione del taglio VEd e considerare la resistenza ultima a taglio come somma di quella dei singoli conci elementari. Ogni concio viene cioè considerato allo stesso modo di una sezione rettangolare le cui resistenze a “taglio trazione” e “taglio compressione” possono essere valutate in base alle relazioni di normativa (4.1.18) e (4.1.19) di seguito riformulate con riferimento al generico concio i ed assumendo le staffe sempre ortogonali all’asse della trave (a = 90°):
VRsd i = 0,9 · di · Asw i /s · fyd ctgq (1)
VRcd i = 0,9 · di · bi · ac · f’cd sinq · cosq (2)
in cui:
di altezza utile del concio i misurata in corrispondenza del perimetro che collega i baricentri delle barre longitudinali;
Asw,i quota parte ideale dell’area delle staffe impegnate dal concio i;
s passo delle staffe;
fyd tensione di snervamento di calcolo delle staffe;
f’cd resistenza a compressione ridotta del calcestruzzo (0,5·fcd);
αc coefficiente maggiorativo per sforzo assiale di compressione;
q angolo di inclinazione delle bielle compresse (uguale per tutti i tralicci elementari).
Perché il singolo concio possa costituire la traccia (sulla sezione trasversale del pilastro) di un elementare traliccio isostatico è necessario che i suoi due estremi ricadano rispettivamente nel corrente compresso del traliccio (zona compressa della sezione per effetto della flessione composta allo SLU) e nel corrente teso costituito dalle barre longitudinali perimetrali. Per soddisfare la prima condizione vengono esclusi i conci non sottesi dall’asse neutro. La seconda condizione può considerarsi soddisfatta se l’armatura longitudinale del pilastro è sufficientemente distribuita lungo il perimetro della sezione (armatura tubolare); per i pilastri si può considerare questa condizione sempre assolta in quanto le NTC prevedono che l’interasse tra le barre longitudinali non sia mai superiore a 25 cm. Nella realtà applicativa il solo soddisfacimento degli elevati valori dei minimi di armatura (r ≥ 1%) porta a progettare interassi tra le barre quasi sempre inferiori al valore massimo indicato. L’Eurocodice 8 prevede, con maggiore severità, un interasse ≤ 15 cm in alta duttilità (DCH) e ≤ 20 cm in media duttilità (DCM).
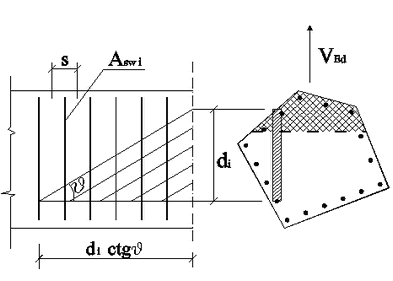
Sulla base delle ipotesi assunte si è rappresentato in figura lo schema longitudinale del traliccio elementare resistente corrispondente al generico concio di altezza utile di.
Per poter valutare compiutamente la resistenza a “taglio trazione” espressa dalla (1) resta da definire Asw i cioè l’area trasversale delle staffe di competenza del generico traliccio elementare. Nella (1) risulta evidente che tale resistenza è direttamente proporzionale all’altezza utile di del concio (considerando costanti tutti gli altri fattori) per cui appare logico assumere:
Asw i = di / Sdi · Asw
Di conseguenza le resistenze a “taglio trazione” e “taglio compressione”, questa volta riferite all’intera sezione, diventano:
VRsd = 0,9 · (Sdi2 / Sdi) Asw /s · fyd · ctgq (3)
VRcd = 0,9 · (S di · bi) · ac · f’cd sinq · cosq (4)
In base alla (4.1.29) delle NTC come resistenza a taglio della trave va assunta quella di minore valore tra le due appena definite.
Le (3) e la (4) sono equivalenti alle corrispondenti formule di normativa (4.1.18) e (4.1.19) a condizione di porre:
d = Sdi2 / Sdi = deq
d · bw = S (di · bi) = Aeq
bw eq = Aeq / deq
I valori bweq deq così ottenuti definiscono, per qualsiasi forma di sezione calcolata, base ed altezza di una sezione rettangolare equivalente ai fini della resistenza ultima a taglio. Tali dimensioni equivalenti consentono, cioè, di utilizzare lo stesso procedimento di verifica a taglio illustrata per le sezioni predefinite.
© Geostru