UNIFORM FLOW HYDRAULICAL VERIFICATION
The hydraulically verification of the section in uniform flow conditions can be done rationally in the artificial canals, where section’s form is regular enough and perturbations are not present .
In the case of the uniform flow the free current inclination and the specific load line fall are equal to the riverbed’s inclination.
The equations that describe the uniform flow are:
Q = cost
![]()
Where:
Q = the flow;
H = current’s total load [m];
if = riverbed’s depth inclination.
In the uniform flowing the medium velocity of the current depend on the riverbed’s characteristics (the inclination, the roughness and the form) and on the currents characteristics (depth, liquid zone area, the hydraulic range) and it is expressed with Chézy’s formula:
![]()
where ih of the load line is equal to the riverbed’s inclination if, R0 is the hydraulic range and C is the roughness coefficient (Strickler, Bazin Kutter,etc.).
Strickler’s expression of the roughness coefficient is:
![]()
where:
c = roughness coefficient;
R = hydraulic range.
Section’s verification problem is that of the guarantee that the project’s flow (high flood’s maximum flow) will pass through the considered section’s interior.
After the computation of the uniform condition’s flow is calculated the liquid height in the section for the calculated flows (that refer to the Recurrence interval.
Generating the energy graphic, corresponding to the user specified flow, the program views the section’s energetically features graphic and the critical height velocity values.
The current’s energy in the section is expressed as follows:
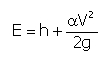
with E measured from the riverbed’s depth elevation.
Its a-synthetic characteristic flowing, for h tending to zero and for h tending to infinite, allows the definition of its minimum point of the k value of the current’s critical height that defines the Q flow.
We must remember, that according to the critical state the current passes from being rapid, with the height h< hcrit, to being slow, with h> hcrit.
So, the critical height of a calculated free current flow Q,is the height h that from where the minimum specified energy E for the riverbed's depth is calculated.