Since most of the geotechnical software is still written in terms of Mohr-Coulomb failure criterion, it is necessary to determine equivalent friction angles and cohesive forces for each rock mass and stress range. This is done by inserting a linear average relationship to the generated curve, solving equation [2] for a range of values of the minor principal stress defined by
![]()
as illustrated in figure 1.
The adaptation process involves balancing the areas above and below the plane of Mohr-Coulomb. This implies the following equations for the angle of friction ![]() and the cohesive force
and the cohesive force ![]() :
:
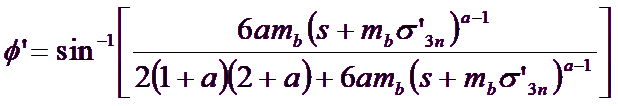 [12]
[12]
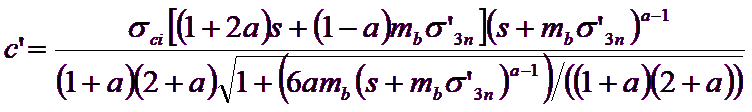 [13]
[13]
where
![]()
Note that the value of ![]() , the upper limit of the confinement stress on which the relationship between the criterion of Hoek-Brown and the Mohr-Coulomb one is considered, must be determined for each individual case.
, the upper limit of the confinement stress on which the relationship between the criterion of Hoek-Brown and the Mohr-Coulomb one is considered, must be determined for each individual case.
The Mohr-Coulomb tangential force ![]() , for a given normal stress
, for a given normal stress ![]() , is obtained by substituting these values of
, is obtained by substituting these values of ![]() and
and ![]() in the equation:
in the equation:
![]() [14]
[14]
The equivalent plane, in terms of major and minor principal stresses, is defined by
![]() [15]
[15]
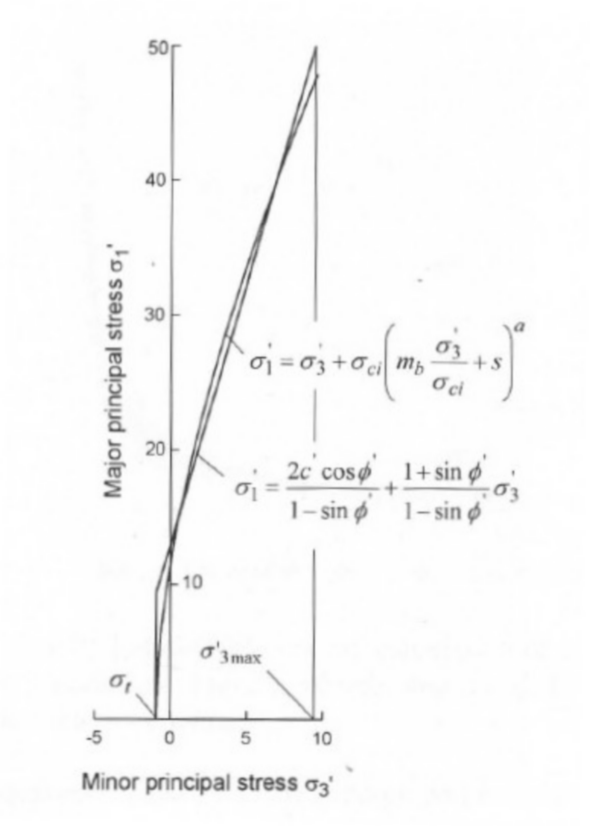
Figure 1: Relations between the major and minor principal stresses for Hoek-Brown and equivalent Mohr-Coulomb criterion
The strength of the rock mass
The uniaxial compressive strength of the rock mass ![]() is given by equation [6]. The failure begins at the edge of an excavation when
is given by equation [6]. The failure begins at the edge of an excavation when ![]() is exceeded by the stress induced by this limit.
is exceeded by the stress induced by this limit.
The failure propagates from this initial point in a field of biaxial stress and it finally stabilizes when the local strength, defined by the equation [2], is the highest of the induced stresses ![]() and
and ![]() . Most of the numerical models are able to follow this process of failure propagation and this level of detailed analysis is very important when considering the stability of excavations in rock and in the design of support systems.
. Most of the numerical models are able to follow this process of failure propagation and this level of detailed analysis is very important when considering the stability of excavations in rock and in the design of support systems.
However, there are times when it is useful to consider the general behavior of a rock mass rather than the process of failure propagation detailed above. For example, when considering the resistance of a pillar, it is more useful to have an estimate of the total resistance of the pillar, rather than a detailed knowledge of the extent of the fracture propagation in the pillar. This leads to the concept of global 'strength of the rock mass' and Hoek and Brown have suggested that this could be estimated from the relationship of Mohr-Coulomb:
![]() [16]
[16]
with ![]() and
and ![]() determined for the stress interval:
determined for the stress interval:
![]()
giving
 [17]
[17]
Determination of 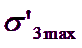
The problem of determining the appropriate value of ![]() to use in the equations 12 and 13 depends on the specific application. Two cases will be studied:
to use in the equations 12 and 13 depends on the specific application. Two cases will be studied:
1. Tunnels - where the value of ![]() is what gives equivalent characteristic curves for the two failure criteria for deep tunnels or equivalent settlement profiles for surface tunnels.
is what gives equivalent characteristic curves for the two failure criteria for deep tunnels or equivalent settlement profiles for surface tunnels.
2. Slopes - here the calculated safety factor and the shape and location of the failure surface must be equivalent.
For the case of deep tunnels, closed-form solutions for both Generalized Hoek-Brown Criterion and Mohr-Coulomb Criterion have been used to generate hundreds of solutions and find the value of ![]() which gives equivalent characteristic curves.
which gives equivalent characteristic curves.
For surface tunnels, where the depth below the surface is less than 3 diameters of excavation, comparative numerical studies of the measurement of failure and surface settlement have given a relationship identical to what was obtained for the deep tunnels, provided that caving in the surface is avoided.
The results of the studies for deep tunnels are represented in Figure 2 and the equation inserted for both cases is:
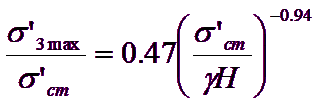 [18]
[18]
where ![]() is the strength of the rock mass, defined by the equation 17,
is the strength of the rock mass, defined by the equation 17, ![]() is the unit weight of the rock mass, H is the depth of the tunnel below the surface. In cases in which the horizontal stress is higher than the vertical one, the value of the horizontal stress should be used instead of
is the unit weight of the rock mass, H is the depth of the tunnel below the surface. In cases in which the horizontal stress is higher than the vertical one, the value of the horizontal stress should be used instead of![]() .
.
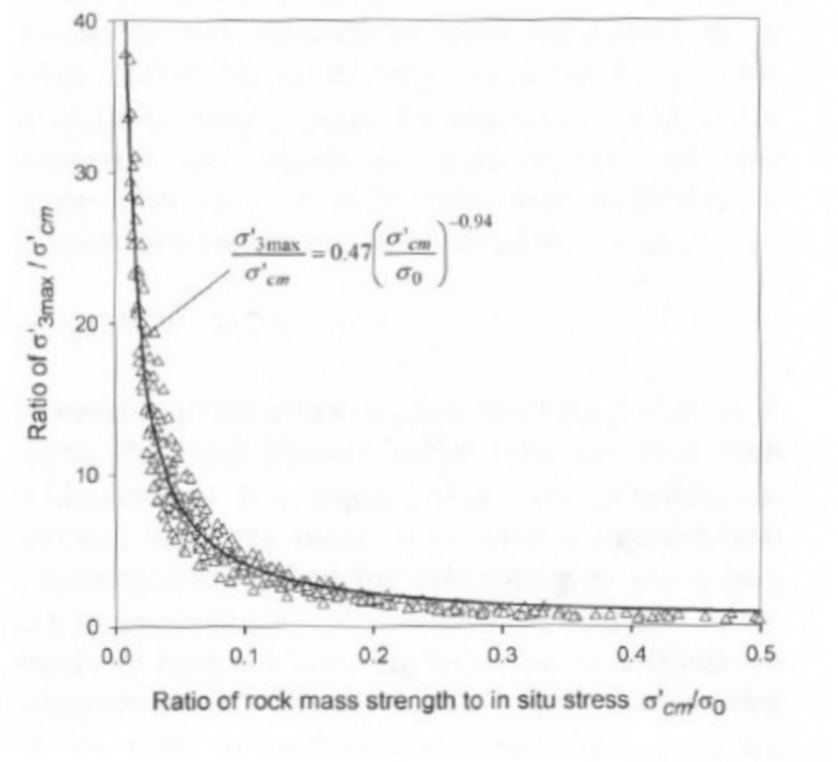
Figure 2: Report for the calculation of![]() for equivalent parameters of Mohr-Coulomb and Hoek-Brown for tunnels.
for equivalent parameters of Mohr-Coulomb and Hoek-Brown for tunnels.
The equation [18] applies to all underground excavations, which are surrounded by a failure zone that does not extend to the surface. For studies on issues such as the blocking of the excavation in the mines is recommended that you do not attempt to correlate the parameters of Hoek-Brown and Mohr-Coulomb, and the determination of the material properties and the subsequent analyzes are based on only one of these criteria.
Similar studies for slopes, using the circular failure analysis of Bishop (1955) for a wide range of slopes geometries and properties of rock masses have given:
 [19]
[19]
where H is the height of the slope.
© GeoStru