Hoek-Brown failure criterion
Hoek and Brown have introduced their failure criterion in an attempt to provide analysis data for the design of underground excavations in hard rock. The criterion was derived from the results of Hoek's research (1968) on the brittle fracture of intact rock and Brown's studies (1970) on the model of the jointed rock mass behavior.
The criterion started from the properties of the intact rock and introduced factors to reduce these properties based on the characteristics of joints in a rock mass. The authors have tried to link the empirical criterion to geological observations by means of one of the rock mass classification schemes available and, to this end, they chose the classification proposed by Bieniawski (1976).
Due to the lack of suitable alternatives, the criterion was soon adopted by the community of rock mechanics and its use quickly spread beyond the original limits used in deriving the relations for strength reduction.
As a result, it has become necessary to review these reports and from time to time introduce new elements because of the wide range of practical problems in which the criterion has been applied. Typical of these improvements have been the introduction of the concept of Hoek and Brown (1997) "undisturbed" and "disturbed" rock masses, and the introduction of a modified criterion to impose to zero the tensile strength of the rock mass for the masses of very poor quality (Hoek, Wood and Shah, 1992).
One of the first difficulties arose from the fact that many geotechnical problems, in particular problems of slope stability are more conveniently discussed in terms of shear and normal stresses rather than with the relationships of the mains stress of the original Hoek-Brown criterion, defined by the equation:
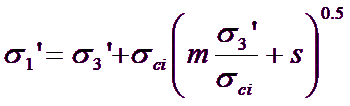[1]
where 
e 
are respectively the major and minor effective stress at main failure 
is the uniaxial compressive strength of the intact rock material and m and s are material constants, where s = 1 for intact rock.
An exact relationship between equation 1 and the normal and tangential failure stresses was obtained Hoek and Bray (1981) and later by Ucar (1986) and Londe (1988).
Hoek has discussed the derivation of equivalent friction angles and cohesive forces for a variety of practical situations. These derivations were based on the tangent to the Mohr envelope obtained by Bray (1981). Hoek suggested that the cohesive strength determined by inserting a tangent to Mohr's curvilinear envelope is an upper limit value and can give optimistic results in the stability calculations. Consequently, an average value, determined by the insertion of a linear relationship Mohr-Coulomb with the method of least squares, may be more appropriate. In this work Hoek has also introduced the concept of Hoek-Brown Generalized Criterion in which the shape of the plane of the main stress or Mohr's envelope could be changed by means of a variable coefficient a instead of the term of the square root in equation 1.
Hoek and Brown have tried to consolidate all previous improvements in a full presentation of the failure criterion and have made a number of concrete examples to illustrate its practical application.
In addition to changes in the equations, it was also recognized that the classification of the rock mass of Bieniawski was no longer adequate as a vehicle for the relationship between the failure criterion and the geological observations in the field, particularly for very weak rock masses. This led to the introduction of the GSI index fo Hoek, Wood and Shah (1992), Hoek (1994) and Hoek, Kaiser and Bawden (1995). This index was subsequently extended for weak rock masses in a series of articles by Hoek, Marinos and Benissi (1998) and Marinos and Marinos and Hoek.
The Generalized Criterion of Hoek-Brown
Is expressed as
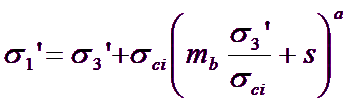[2]
where mb is a reduced value of the material constant mi and is given by
[3]
s and a are constants for the rock mass:
[4]
[5]
D is a factor that depends on the disturbance degree to which the rock mass is subjected by blast damage and stress relaxation. It varies from 0 for undisturbed in situ rock masses to 1 for very disturbed rock masses (see Guidelines for the estimation of the disturbance D).
The uniaxial compressive strength is obtained by setting in equation [2]
providing
[6]
and the tensile strength is given by:
[7]
The equation [7] was obtained imposing
in the equation [2]. This represents a condition of the biaxial stress. Hoek has shown that, for brittle materials, the uniaxial tensile strength is equal to the biaxial tensile strength.
Note that the 'transition' to GSI = 25 for the coefficients s and a was eliminated in equations 4 and 5 which give continuous uniform transitions throughout the entire range of GSI values. The numerical values of a and s, given by these equations, are very similar to those given by the previous equations.
The normal and shear stresses are related to the principal stresses through the equations published by Balmer.
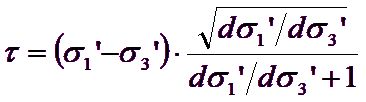[9]
[10]
Deformation modulus
The deformation modulus of the rock mass is given by:
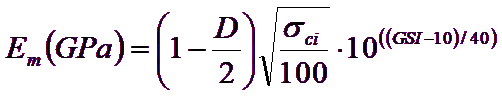[11a]
The equation 11a is valid for
For
is used the equation 11b.
[11b]
Note that the original equation proposed by Hoek and Brown has been changed, with the inclusion of the factor D, to allow the effects of the explosion damage and the stress relaxation.
© GeoStru