The bearing capacity of shallow foundations on rock applying methods based on the failure criterion of Hoek and Brown
The verification to limit states of the "soil-foundation" complex according to the new legislation, concerns the assessment of the failure mechanisms determined by the mobilization of the overall strength of the materials. In particular, for each ultimate limit state the following condition must be respected:
Ed ≤ Rd
where Ed is the design value of the action or of the effect of the action, Rd is the design value of the geotechnical system strength.
In this case, the foundations are made of rectangular elements with small size of 3.0 m amounted to a depth of 1.5 m below ground level, or directly resting on the rocky metarenite substrate.
For verification, since the foundation soils are stony rocks although fractured, reference was made to the calculation methods proposed by Carter and Kulhawy (1988) and by Serrano, Olalla and Gonzalez (2000), both based on the failure criterion of Hoek and Brown, valid just for shallow foundations on stone materials.
Method of Carter & Kulhawy
The ultimate bearing capacity of a rock mass can be written in the form:
[20]
where 
is the unconfined compressive strength of the intact rock and 
is defined as bearing capacity factor. According to this criterion, the ultimate bearing capacity of a rock mass is considered as a "fraction" of the uniaxial compressive strength of the intact rock.
The resolution of Carter and Kulhawy refers to the theorem of the lower limit, in which the stresses state must satisfy the equilibrium and must not violate the plasticity conditions. The resolution of the problem can be achieved by examining a load condition in which the rock mass is considered as devoid of weight and is divided into two zones; in particular in zone I, the rock being devoid of weight, the minor principal stress 
coincides with the vertical direction, while the major principal stress 
coincides with the horizontal direction. In this zone the value of the principal stress 
is obtained from the general equation [2] by putting 
and corresponds to the unconfined compression strength resistance to compressive of the rock mass.
[21]
In zone II, ie below the foundational structure, the 
is vertical and is equal to qu (ultimate bearing capacity), while 
, since the equilibrium along the contact between zone I and zone II must be maintained, assumes the value shown in equation 21.
Replacing the values of 
and 
shown in the formula of the general failure criterion of Hoek and Brown, in correspondence of zone II is:
By simplifying and putting 
in evidence, we obtain:
[22]
Equation [22] can be made consistent with the 20 puting:
Where the symbol 
indicates that the rock mass is considered to be devoid of weight. Equation [22, with the various parameters calculated according to the types of rock masses presented by Hoek and Brown, is used to produce the computation guidelines for the bearing capacity of shallow foundations in rock masses in "AASHTO - Standard specification for highway bridges."
Method of Serrano, Olalla and Gonzalez
Serrano and Olalla (1998) and Serrano, Olalla and Gonzalez (2000) have proposed a method for estimating the ultimate bearing capacity of shallow foundations on rock masses. The calculation is based on the theory of slip line developed by Sokolowsky and also uses the criterion developed by Hoek and Brown. The expression that allows the computation of the ultimate bearing capacity is the following:
[23]
where 
and
are constants of the rock mass that depend on mb, 
, s and 
according to the following expressions:
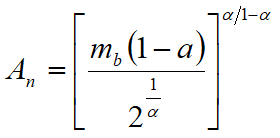
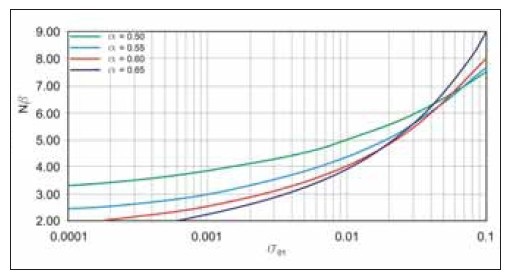
The factor 
can be determined graphically using the abacus provided by Serrano et al. (2001), shown in the following figure:
© GeoStru