Indice n (Jasarevic & Kovacevic)
Il metodo è stato sviluppato sulle formazioni carbonatiche della Croazia ed ha una evidente derivazione dal sistema RMR. Il sistema di classificazione è semplice e si sviluppa attribuendo almeno tre coefficienti numerici relativi a proprietà geomeccaniche dell’ammasso roccioso e di almeno altrettanti relativi a proprietà geologico-ingegneristiche.
Ad ogni parametro viene assegnato un valore ni variabile da 1 a 5 come riportato nella seguente tabella:
PROPRIETA' GEOMECCANICHE
|
PROPRIETA' GEOLOGICO-INGEGNERISTICHE |
ni |
|||||||||
Su (MPa) |
Is ⊥ (MPa) |
Is // (MPa) |
Vp (km/s) |
Vp/V0 |
α |
Acqua |
RQD (%) |
Jv |
S (cm) |
Proprietà dei giunti |
|
> 130 |
> 5,7 |
> 0,8 |
> 6,5 |
>0, 8 |
70-90 |
A |
> 65 |
1-2 |
> 50 |
JRC: 16-20 |
1 |
100-130 |
5,3-5,7 |
0,7-0,8 |
4,7-6,5 |
0,6-0,8 |
0-20 |
U |
45-65 |
2-5 |
20-50 |
JRC: 12-16 |
2 |
70-100 |
4,7-5,3 |
0,6-0,7 |
3,0-4,7 |
0,4-0,6 |
20-35 |
B |
35-45 |
5-10 |
10-20 |
JRC: 8-12 |
3 |
40-70 |
4,3-4,7 |
0,5-0,6 |
1,2-3,0 |
0,2-0,4 |
35-50 |
S |
25-35 |
10-15 |
6-10 |
JRC: 4-8 |
4 |
< 40 |
< 4,3 |
< 0,5 |
<1,2 |
<0,2 |
50-70 |
F |
<25 |
>15 |
<6 |
JRC: <4 o riempiti |
5 |
dove:
Su = resistenza a compressione uniassiale della roccia intatta;
Is ⊥ = indice point load misurato perpendicolarmente alla discontinuità principale;
Is // = indice point load misurato parallelamente alla discontinuità principale;
Vp = velocità sismica delle onde longitudinali;
V0 = velocità sismica di riferimento (roccia intatta) delle onde longitudinali;
α = inclinazione della discontinuità più sfavorevole;
Acqua = A: assente – U: umido – B: bagnato – S: deboli venute – F: forti venute;
Jv = numero di giunti per m3;
S = spaziatura delle discontinuità.
Se i valori non sono univoci si prende il coefficiente numerico intermedio, ad esempio per Jv variabile fra 5 e 15 si prende 3,5.
Quindi il valore delliindice n sarà dato dalla:
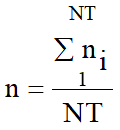
dove NT è il numero delle proprietà considerate (minimo 6) nell'attribuzione dei coefficienti numerici.
Gli autori suggeriscono inoltre la seguente correlazione fra n e RMRc:
RMRc = 110 – 20n
Dal calcolo di RMR è possibile derivare la classe e la qualità dell'ammasso, simile a quella di Beniawsky:
RMRC |
100-81 |
80-61 |
60-41 |
40-21 |
<=20 |
Classe |
I |
II |
III |
IV |
V |
Descrizione |
Molto buono |
Buono |
Mediocre |
Scadente |
Pessimo |
Dal valore di RMRc si derivano i parametri caratteristici dell’ammasso con le seguenti:
c (kPa) = 3,625 RMRc (Sen)
ϕ (°) = 25 (1 + 0,01 RMRc) per RMRc > 20 (Sen)
ϕ (°) = 1,5 RMRc per RMRc < 20 (Sen)
E (MPa) = Exp(4,407 + 0,081 RMRc) (Jasarevic & Kovacevic)
Gli autori ritengono che la formula utilizzata per il calcolo di E sia più corretta rispetto a quella di Serafim e Pereira (1983):
E (GPa) = 10(RMRb – 10 / 40)
© GeoStru